图像二维离散小波变换
这两天接触图像多尺度分解的一些内容,主要重点在EMD(empirical mode decomposition)——BEMD(bidimensional empirical mode decomposition),LMD(local mean decomposition)——BLMD(bidimensional local mean decomposition,BLMD)。
之前一直没有接触过这个领域,现在开始慢慢做一些积累,先从小波变换开始吧。
1 图像多尺度分解
由于图像对象尺寸大小的不一,以及人类视觉系统对物体尺度的自适应性,在图像数据中引入一个尺度维,把图像在不同尺度下进行分解。直观地来讲,客观的物体根据其与观察者的距离远近不同而呈现出不同的表现形式,比如,人在不同的距离观察同一目标对象时,在距离较远时,看到的是对象的整体轮廓,在近距离观察时,看到的是关于对象的更多的细节,便是对图像进行了多尺度分解。
目前关于图像多尺度分解中的“尺度”一词,存在多种不同的直观理解,如把图像的分辨率作为图像分解的尺度,或以图像对象尺寸大小作为图像分解的尺度,又或以对图像进行卷积的卷积核的参数作为图像分解的尺度。
2 图像二维离散小波变换
图像的二维离散小波分解和重构过程如下图所示,分解过程可描述为:首先对图像的每一行进行 1D-DWT,获得原始图像在水平方向上的低频分量 L 和高频分量 H,然后对变换所得数据的每一列进行 1D-DWT,获得原始图像在水平和垂直方向上的低频分量 LL、水平方向上的低频和垂直方向上的高频 LH、水平方向上的高频和垂直方向上的低频 HL 以及水平和垂直方向上的的高频分量 HH。重构过程可描述为:首先对变换结果的每一列进行以为离散小波逆变换,再对变换所得数据的每一行进行一维离散小波逆变换,即可获得重构图像。由上述过程可以看出,图像的小波分解是一个将信号按照低频和有向高频进行分离的过程,分解过程中还可以根据需要对得到的 LL 分量进行进一步的小波分解,直至达到要求。
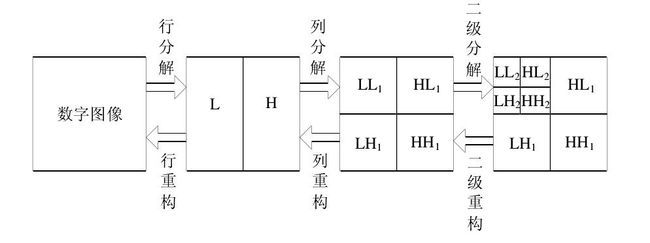
备注:为了直观地体现小波多尺度分解,下面在matlab里做了一组测试,简单代码如下:
load woman;
% X包含图像
% 图像分解尺度为2,采用sym5小波
[c,s] = wavedec2(X,2,'sym5');
%分解尺度为1的低频分量
a1 = wrcoef2('a',c,s,'sym5',1);
%分解尺度为2的低频分量
a2 = wrcoef2('a',c,s,'sym5',2);
%%高频分量
%HL
hd2 = wrcoef2('h',c,s,'sym5',2);
%LH
vd2 = wrcoef2('v',c,s,'sym5',2);
%HH
dd2 = wrcoef2('d',c,s,'sym5',2);
M=[a2 hd2;vd2 dd2];
image(M);colormap(map);
axis off;
%%%继续对LL进行分解
[c,s] = wavedec2(a2,2,'sym5');
a22 = wrcoef2('a',c,s,'sym5',2);
hd22 = wrcoef2('h',c,s,'sym5',2);
vd22 = wrcoef2('v',c,s,'sym5',2);
dd22 = wrcoef2('d',c,s,'sym5',2);
figure(2);
N=[a22 hd22;vd22 dd22];
image(N);colormap(map);
axis off;
备注:在图像完成分解后,如何分析才是需要继续研读的重点。

