TensorFlow-深度学习-10-DropOut与多层神经网络
对于简单的3层人工神经网络,常用的激活函数很容易达到饱和度,比如sigmod,因为它很容易达到一个饱和度,导致整个训练终止。我之前在三层人工神经网络上加了一层,变成4层,然后进行训练,但是发现,训练的结果并没有什么变化,这是因为4层人工神经网络可能已经存在了过拟合的现象。
其实经过大量研究人员的研究发现,三层神经网络其实已经能够满足比较大的数据量的训练,再增加其实已经没有什么意义了。所以要增加隐藏层根本没有什么实际意义,那如果我们真的想要训练的结果再高一点怎么办?所以伟大的研究人员提出了DropOut方法。训练的时候让每层的神经元都不一定要全部参与计算,可以随机选择每层神经元节点进行计算。但是测试的时候,就让每层的所有神经元节点参与计算,这样训练速度快了,测试结果也提高了。
下图是一张标准的四层神经网络:
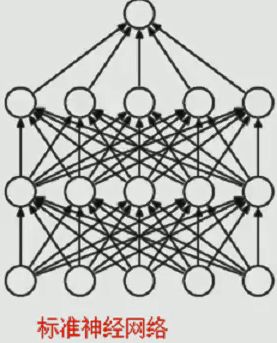
但是,4层与三层的训练结果差不了太多,所以引入dropout方法,如下图:
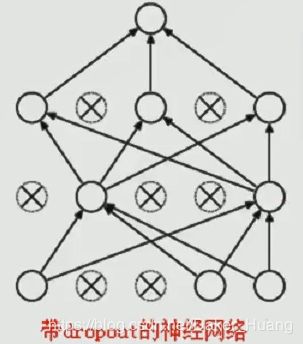
上图带drop的神经网络会随机选择每层的神经元节点(我们需要自己设置节点数的百分比),然后就可以开始训练。**注意:训练时选择部分神经元节点,但测试时需要所有神经元节点的参与。每层神经元节点上的权重相加为1。**如下:
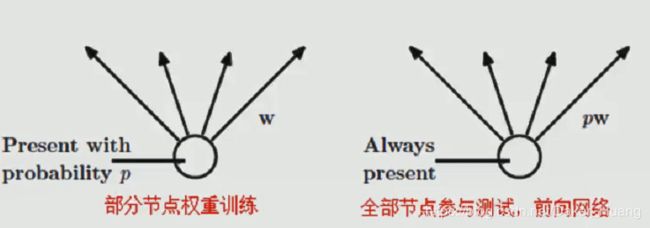
实例(四层神经网络):
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("mnist/", one_hot=True)
'''mnist数据集图片是28*28大小,故有784个元素块'''
def dropout_MLP():
hidden_num1 = 100
hidden_num2 = 100
dropout_value = tf.placeholder(dtype=tf.float32) #参与节点的数目百分比
x = tf.placeholder(shape=[None, 784], dtype=tf.float32) # 输入值
y = tf.placeholder(shape=[None, 10], dtype=tf.float32) # 真实值
# -------输入层与第一层隐层权值与偏执项-----------
w1 = tf.Variable(tf.truncated_normal(shape=[784, hidden_num1]), dtype=tf.float32)
b1 = tf.Variable(tf.truncated_normal(shape=[1, hidden_num1]), dtype=tf.float32)
# ---------第一层隐层与第二层隐层权值与偏执项-----------
w2 = tf.Variable(tf.truncated_normal(shape=[hidden_num1, hidden_num2]), dtype=tf.float32)
b2 = tf.Variable(tf.truncated_normal(shape=[1, hidden_num2]), dtype=tf.float32)
# ---------第二次隐层与输出层权值与偏执项-----------
w3 = tf.Variable(tf.truncated_normal(shape=[hidden_num2, 10]), dtype=tf.float32)
b3 = tf.Variable(tf.truncated_normal(shape=[1, 10]), dtype=tf.float32)
# 第一次计算
nn1 = tf.add(tf.matmul(x, w1), b1) # dropout随机节点训练
out1 = tf.nn.dropout(tf.sigmoid(nn1), keep_prob=dropout_value) #dropout
# 第二次计算
nn2 = tf.add(tf.matmul(out1, w2), b2)
out2 = tf.nn.dropout(tf.sigmoid(nn2), keep_prob=dropout_value)
# 第三次计算
nn3 = tf.add(tf.matmul(out2, w3), b3)
out3 = tf.sigmoid(nn3)
# loss计算
loss_L2 = tf.reduce_sum(tf.square(tf.subtract(y, out3))) # L2损失
# 梯度下降-反向传播(BP)
step = tf.train.GradientDescentOptimizer(learning_rate=0.05).minimize(loss_L2)
acc_mat = tf.equal(tf.argmax(y, 1), tf.argmax(out3, 1)) # 准确率
acc_ret = tf.reduce_sum(tf.cast(acc_mat, dtype=tf.float32)) # 类型转换
init = tf.global_variables_initializer()
with tf.Session() as sess:
loss_array=[]
test_ratio=[]
sess.run(init)
for i in range(20000):
batch_xs, batch_ys = mnist.train.next_batch(128) # 设置每次训练样本数batch
sess.run(step, feed_dict={x: batch_xs, y: batch_ys,dropout_value:0.8})
acc_test, curr_loss = sess.run([acc_ret, loss_L2],
feed_dict={x: mnist.test.images[:1000], y: mnist.test.labels[:1000],
dropout_value: 1.0})
loss_array.append(curr_loss)
test_ratio.append(acc_test/10)
if (i + 1) % 2000 == 0:
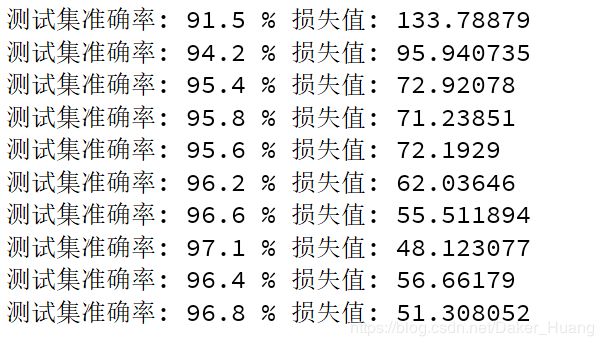
print("测试集准确率:", (acc_test / 10), "%","损失值:",curr_loss)
fig=plt.figure() #创建图片
ax1=fig.add_subplot(1,2,1) #显示损失值
ax2=fig.add_subplot(1,2,2) #显示测试集准确率
# ------损失值图形--------
ax1.plot(loss_array,"r--")
ax1.set_title("loss value")
# ------测试集准确率图形--------
ax2.plot(test_ratio,"b--")
ax2.set_title("test accuary")
plt.show()
if __name__ == "__main__":
dropout_MLP()
结果:
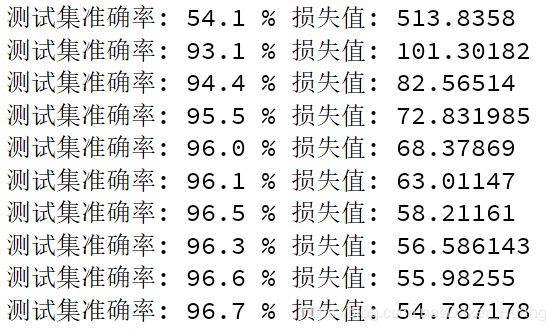
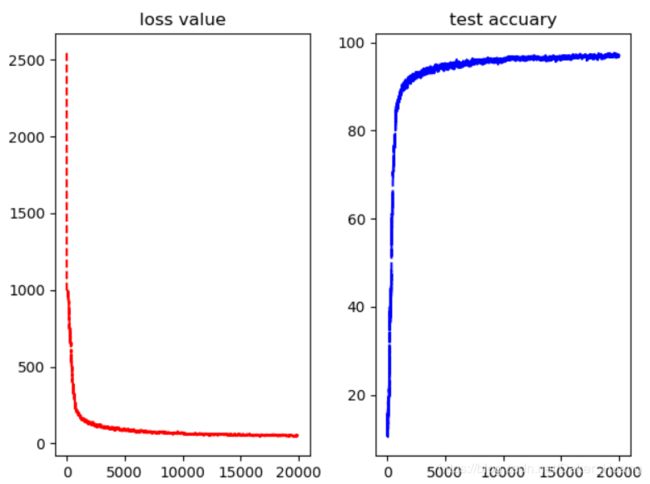
图像如下:
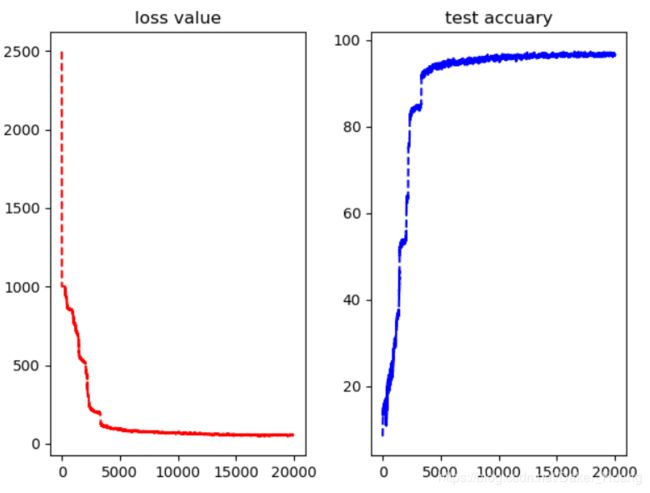
可以看到,最高达到了块97%,之前的文章中没有加入dropout方法时也只有94%左右的准确率。
当我将网络升为5层(只增加1层数,其余参数不变)后,实例代码如下:
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("mnist/", one_hot=True)
'''mnist数据集图片是28*28大小,故有784个元素块'''
def dropout_MLP():
hidden_num1 = 100
hidden_num2 = 100
hidden_num3 = 50
dropout_value = tf.placeholder(dtype=tf.float32) # 参与节点的数目百分比
x = tf.placeholder(shape=[None, 784], dtype=tf.float32) # 输入值
y = tf.placeholder(shape=[None, 10], dtype=tf.float32) # 真实值
# -------输入层与第一层隐层权值与偏执项-----------
w1 = tf.Variable(tf.truncated_normal(shape=[784, hidden_num1]), dtype=tf.float32)
b1 = tf.Variable(tf.truncated_normal(shape=[1, hidden_num1]), dtype=tf.float32)
# ---------第一层隐层与第二层隐层权值与偏执项-----------
w2 = tf.Variable(tf.truncated_normal(shape=[hidden_num1, hidden_num2]), dtype=tf.float32)
b2 = tf.Variable(tf.truncated_normal(shape=[1, hidden_num2]), dtype=tf.float32)
# ---------第二次隐层与第三次隐层权值与偏执项-----------
w3 = tf.Variable(tf.truncated_normal(shape=[hidden_num2, hidden_num3]), dtype=tf.float32)
b3 = tf.Variable(tf.truncated_normal(shape=[1, hidden_num3]), dtype=tf.float32)
# ---------第三次隐层与输出层权值与偏执项-----------
w4 = tf.Variable(tf.truncated_normal(shape=[hidden_num3, 10]), dtype=tf.float32)
b4 = tf.Variable(tf.truncated_normal(shape=[1, 10]), dtype=tf.float32)
# 第一次计算
nn1 = tf.add(tf.matmul(x, w1), b1) # dropout随机节点训练
out1 = tf.nn.dropout(tf.sigmoid(nn1), keep_prob=dropout_value) # dropout
# 第二次计算
nn2 = tf.add(tf.matmul(out1, w2), b2)
out2 = tf.nn.dropout(tf.sigmoid(nn2), keep_prob=dropout_value)
# 第三次计算
nn3 = tf.add(tf.matmul(out2, w3), b3)
out3 = tf.nn.dropout(tf.sigmoid(nn3),keep_prob=dropout_value)
# 第四次计算
nn4 = tf.add(tf.matmul(out3, w4), b4)
out4 = tf.sigmoid(nn4)
# loss计算
loss_L2 = tf.reduce_sum(tf.square(tf.subtract(y, out4))) # L2损失
# 梯度下降-反向传播(BP)
step = tf.train.GradientDescentOptimizer(learning_rate=0.05).minimize(loss_L2)
acc_mat = tf.equal(tf.argmax(y, 1), tf.argmax(out4, 1)) # 准确率
acc_ret = tf.reduce_sum(tf.cast(acc_mat, dtype=tf.float32)) # 类型转换
init = tf.global_variables_initializer()
with tf.Session() as sess:
loss_array = []
test_ratio = []
sess.run(init)
for i in range(20000):
batch_xs, batch_ys = mnist.train.next_batch(128) # 设置每次训练样本数batch
sess.run(step, feed_dict={x: batch_xs, y: batch_ys, dropout_value: 0.8})
acc_test, curr_loss = sess.run([acc_ret, loss_L2],
feed_dict={x: mnist.test.images[:1000], y: mnist.test.labels[:1000],
dropout_value: 1.0})
loss_array.append(curr_loss)
test_ratio.append(acc_test / 10)
if (i + 1) % 2000 == 0:
print("测试集准确率:", (acc_test / 10), "%", "损失值:", curr_loss)
fig = plt.figure() # 创建图片
ax1 = fig.add_subplot(1, 2, 1) # 显示损失值
ax2 = fig.add_subplot(1, 2, 2) # 显示测试集准确率
# ------损失值图形--------
ax1.plot(loss_array, "r--")
ax1.set_title("loss value")
# ------测试集准确率图形--------
ax2.plot(test_ratio, "b--")
ax2.set_title("test accuary")
plt.show()
if __name__ == "__main__":
dropout_MLP()