UFLDL——Exercise: Sparse Autoencoder 稀疏自动编码
实验要求可以参考deeplearning的tutorial,Exercise:Sparse Autoencoder。稀疏自动编码的原理可以参照之前的博文,神经网络, 稀疏自动编码 。
1. 神经网络结构:
实验是实现三层的稀疏自动编码神经网络,神经网络结构包括输入层64个neuron,隐含层25个neuron(都不包括bias结点),输出层和输入层相同的neuron的个数。
2. 训练数据:
实验中的原始数据是10副512×512大小的灰度图像,存储在“IMAGES.mat”文件中。下图是其中的一张图像。
我们随机中10副图像中挑选一个,然后再从该图像中随机的选一个8*8的图像patch,得到的这个patch作为一个训练数据,重复这个随机过程10000,最后得到10000数据组成的训练集,存储在64×10000 的矩阵,每一列代表一个数据。
下图是总10000个数据中随机挑选出100个进行显示。
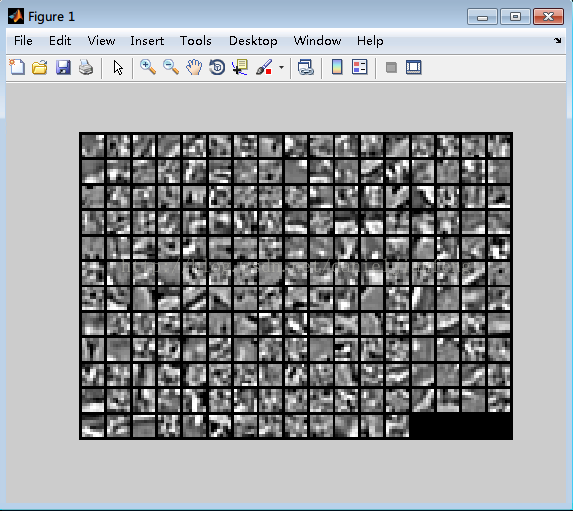
3. 损失函数(loss function)
稀疏自动编码的损失函数由三部分组成,公式如下:
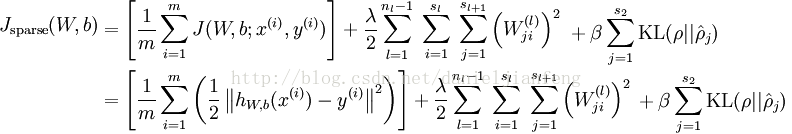
4. 偏导数(partial derivatives)
偏导数的计算是通过BP算法,需要注意是,由于在实验中使用的是batch的优化方法,所以偏导数计算的时候对所有样本的偏导数做了一个求和操作。
5.梯度检验(Gradient checking)
有网友说他们在自己的电脑上跑Gradient checking这步的时候用了1个多小时,但不知道是不是我的电脑配置比较高,我才跑了不到4分钟。
6. 用L-BFGS算法进行训练
因为我们已经有了损失函数和相应参数的偏导数,所以和直接用成熟的L-BFGS算法的包,最后算法到底最大迭代次数400的时候,停止迭代。

7. 实验结果:
下图显示的是第一层到第二层的参数,由于输入层为64个neuron,隐含层为25个neuron,所以下面共有25个patch,每一个patch大小为8*8.
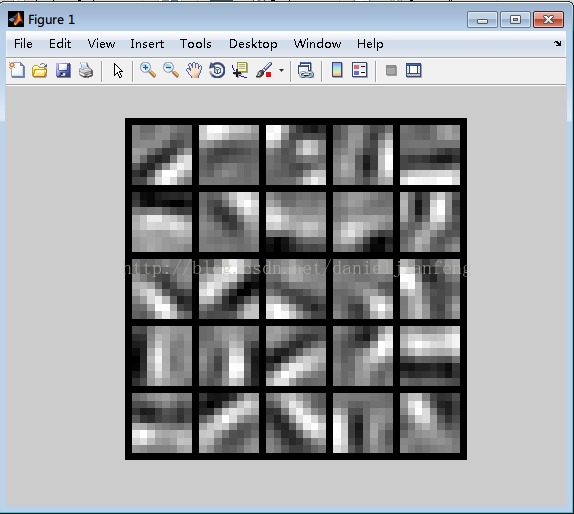
源代码下载
sampleIMAGES.m
function patches = sampleIMAGES()
% sampleIMAGES
% Returns 10000 patches for training
load IMAGES; % load images from disk
patchsize = 8; % we'll use 8x8 patches
numpatches = 10000;
% Initialize patches with zeros. Your code will fill in this matrix--one
% column per patch, 10000 columns.
patches = zeros(patchsize*patchsize, numpatches);
%% ---------- YOUR CODE HERE --------------------------------------
% Instructions: Fill in the variable called "patches" using data
% from IMAGES.
%
% IMAGES is a 3D array containing 10 images
% For instance, IMAGES(:,:,6) is a 512x512 array containing the 6th image,
% and you can type "imagesc(IMAGES(:,:,6)), colormap gray;" to visualize
% it. (The contrast on these images look a bit off because they have
% been preprocessed using using "whitening." See the lecture notes for
% more details.) As a second example, IMAGES(21:30,21:30,1) is an image
% patch corresponding to the pixels in the block (21,21) to (30,30) of
% Image 1
for i = 1:numpatches
x = ceil(rand(1)*505);
y = ceil(rand(1)*505);
z = ceil(rand(1)*10);
patch = IMAGES(x : x+patchsize-1, y : y+patchsize-1, z);
patches(:,i) = patch(:);
end
%% ---------------------------------------------------------------
% For the autoencoder to work well we need to normalize the data
% Specifically, since the output of the network is bounded between [0,1]
% (due to the sigmoid activation function), we have to make sure
% the range of pixel values is also bounded between [0,1]
patches = normalizeData(patches);
end
%% ---------------------------------------------------------------
function patches = normalizeData(patches)
% Squash data to [0.1, 0.9] since we use sigmoid as the activation
% function in the output layer
% Remove DC (mean of images).
patches = bsxfun(@minus, patches, mean(patches));
% Truncate to +/-3 standard deviations and scale to -1 to 1
pstd = 3 * std(patches(:));
patches = max(min(patches, pstd), -pstd) / pstd;
% Rescale from [-1,1] to [0.1,0.9]
patches = (patches + 1) * 0.4 + 0.1;
end
sparseAutoencoderCost.m
function [cost,grad] = sparseAutoencoderCost(theta, visibleSize, hiddenSize, ...
lambda, sparsityParam, beta, data)
% visibleSize: the number of input units (probably 64)
% hiddenSize: the number of hidden units (probably 25)
% lambda: weight decay parameter
% sparsityParam: The desired average activation for the hidden units (denoted in the lecture
% notes by the greek alphabet rho, which looks like a lower-case "p").
% beta: weight of sparsity penalty term
% data: Our 64x10000 matrix containing the training data. So, data(:,i) is the i-th training example.
% The input theta is a vector (because minFunc expects the parameters to be a vector).
% We first convert theta to the (W1, W2, b1, b2) matrix/vector format, so that this
% follows the notation convention of the lecture notes.
W1 = reshape(theta(1:hiddenSize*visibleSize), hiddenSize, visibleSize);
W2 = reshape(theta(hiddenSize*visibleSize+1:2*hiddenSize*visibleSize), visibleSize, hiddenSize);
b1 = theta(2*hiddenSize*visibleSize+1:2*hiddenSize*visibleSize+hiddenSize);
b2 = theta(2*hiddenSize*visibleSize+hiddenSize+1:end);
% Cost and gradient variables (your code needs to compute these values).
% Here, we initialize them to zeros.
cost = 0;
W1grad = zeros(size(W1));
W2grad = zeros(size(W2));
b1grad = zeros(size(b1));
b2grad = zeros(size(b2));
%% ---------- YOUR CODE HERE --------------------------------------
% Instructions: Compute the cost/optimization objective J_sparse(W,b) for the Sparse Autoencoder,
% and the corresponding gradients W1grad, W2grad, b1grad, b2grad.
%
% W1grad, W2grad, b1grad and b2grad should be computed using backpropagation.
% Note that W1grad has the same dimensions as W1, b1grad has the same dimensions
% as b1, etc. Your code should set W1grad to be the partial derivative of J_sparse(W,b) with
% respect to W1. I.e., W1grad(i,j) should be the partial derivative of J_sparse(W,b)
% with respect to the input parameter W1(i,j). Thus, W1grad should be equal to the term
% [(1/m) \Delta W^{(1)} + \lambda W^{(1)}] in the last block of pseudo-code in Section 2.2
% of the lecture notes (and similarly for W2grad, b1grad, b2grad).
%
% Stated differently, if we were using batch gradient descent to optimize the parameters,
% the gradient descent update to W1 would be W1 := W1 - alpha * W1grad, and similarly for W2, b1, b2.
%
% data = [ones(1,size(data,2)); data];
[n m] = size(data);
z2 = W1* data + repmat(b1,1,m);
a2 = sigmoid(z2);
z3 = W2 * a2 + repmat(b2,1,m);
a3 = sigmoid(z3);
phat = mean(a2,2);
p = repmat(sparsityParam, size(phat));
sparse = p .* log(p ./ phat) + (1-p) .* log((1-p) ./ (1-phat));
%J = trace((data - a3)' * (data - a3)) / (size(data,2)*2);
J = sum(sum((a3-data).^2)) / (m*2);
regu = (W1(:)'*W1(:) + W2(:)'*W2(:))/2;
cost = J + lambda*regu + beta * sum(sparse);
delta3 = -1* (data-a3).*a3.*(1-a3);
delta2 = (W2'*delta3+beta*repmat(-p./phat+(1-p)./(1-phat),1,size(data,2))).*a2.*(1-a2);
W2grad = delta3*a2'/m;
b2grad = mean(delta3,2);
W1grad = delta2*data'/m;
b1grad = mean(delta2,2);
W2grad = W2grad + lambda*W2;
W1grad = W1grad + lambda*W1;
%-------------------------------------------------------------------
% After computing the cost and gradient, we will convert the gradients back
% to a vector format (suitable for minFunc). Specifically, we will unroll
% your gradient matrices into a vector.
grad = [W1grad(:) ; W2grad(:) ; b1grad(:) ; b2grad(:)];
end
%-------------------------------------------------------------------
% Here's an implementation of the sigmoid function, which you may find useful
% in your computation of the costs and the gradients. This inputs a (row or
% column) vector (say (z1, z2, z3)) and returns (f(z1), f(z2), f(z3)).
function sigm = sigmoid(x)
sigm = 1 ./ (1 + exp(-x));
end