AVL树
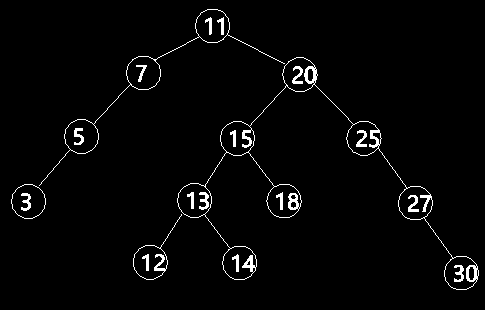
普通二叉搜索树可能出现一条分支有多层,而其他分支却只有几层的情况,如图1所示,这会导致添加、移除和搜索树具有性能问题。因此提出了自平衡二叉树的概念,AVL树(阿德尔森-维尔斯和兰迪斯树)是自平衡二叉树的一种,AVL树的任一子节点的左右两侧子树的高度之差不超过1,所以它也被称为高度平衡树。
图1
要将不平衡的二叉搜索树转换为平衡的AVL树需要对树进行一次或多次旋转,旋转方式分为左单旋、右单旋、左-右双旋、右-左双旋。
左单旋
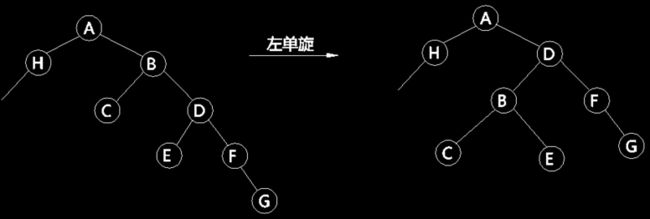
对某一节点B(图2)做左单旋,处理过程相当于,断开B与父节点A的连接,将B的右子节点D与A连接,将B作为D的左子节点,将D的左子节点E作为B的右子节点。以图1的二叉树为例,对键值为15的节点做左单旋,首先断开15与11的连接,再将20与11连接,将15作为20的左子节点,最后将18作为15的右子节点;可以想象为以15为中心做了一定的逆时针旋转。结果如图3。
图2
图3
再看图2,根据搜索二叉树的性质,肯定有D>B>A,E>B,因此旋转过后,能够保证 右子节点 > 父节点 > 左子节点,不会破坏树的结构。
可以看到,一次左单旋将右侧子树的高度减小了1,而左侧子树的高度增加了1。实现代码如下:
function roateLeft(AvlNode) {
var node = AvlNode.right; // 保存右子节点
AvlNode.right = node.left; // node的左子节点连接到AvlNode成为其右子节点
node.left = AvlNode; // AvlNode连接到node成为其左子节点
return node; // 返回node,连接到AvlNode最初的父节点
}右单旋
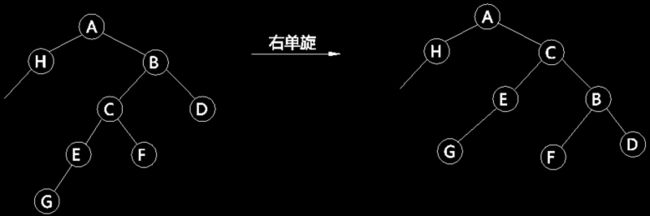
右单旋与左单选类似,以某一节点B(图4)做右单旋,首先断开B与其父节点A的连接,将B的左子节点C与A连接,将C的右子节点F作为B的左子节点。同样的,因为有C>A,B>F>C,因此旋转过后,不会破坏树的结构。可以看到,一次右单旋使节点的左侧子树高度减小了1,而右侧子树的高度增加了1。
图4
实现代码如下:
function roateRight(AvlNode) {
var node = AvlNode.left; // 保存左子节点
AvlNode.left = node.right; // 将node的右子节点连接到AvlNode成为其左子节点
node.right = AvlNode; // AvlNode连接到node,成为其右子节点
return node; // 返回node连接到AvlNode最初的父节点
}左-右双旋
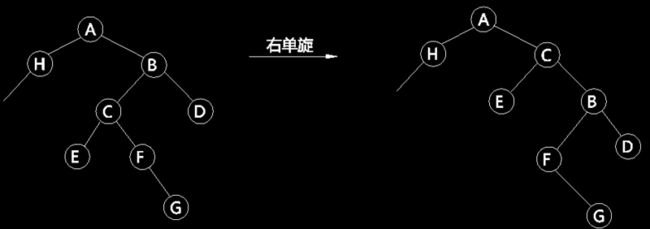
左单旋、右单旋在某些情况下是不能达到平衡树的目的的。如图4,对B进行右单旋,需要左子树C的右子树F的高度小于等于左子树E的高度,否则不能达到平衡的效果,只是把不平衡性从左边转移到了右边。图5演示了这种情况。同样的,左单旋也有这个问题。
图5
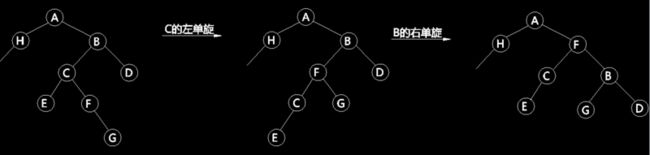
因此为了达到目的,需要先对旋转节点的左子节点做左单旋,再对旋转节点做右单旋。如图6所示,先对节点B的左子节点C做左单旋,可以看到,这个操作,相当于将节点C的不平衡性从右侧转移到了左侧,从而满足了上述右单旋的条件;最后再对B节点做右单旋操作,最终达到了平衡的目的。
图6
实现代码如下:
function roateLeftRight(AvlNode) {
AvlNode.right = roateLeft(AvlNode.right); // 对右子节点做左单旋
return roateRight(AvlNode); // 做右单旋
}右-左双旋
同理,如图2,对B进行左单旋时,需要右子树D的右子树F的高度大于等于左子树E的高度,否则需要进行双旋;即先对B的右子节点D做右单旋,再对B做左单旋。实现代码如下:
function roateRightLeft(AvlNode) {
AvlNode.left = roateRight(AvlNode.left); // 对左子节点做右单旋
return roateLeft(AvlNode); // 做左单旋
}实现树的平衡
首先实现获取树高度的函数:
function getAvlTreeHeight(node) {
if (node == null) {
// node不存在返回0
return 0;
} else {
var leftHeight = getAvlTreeHeight(node.left);
var rightHeight = getAvlTreeHeight(node.right);
// 返回左子树、右子树中的最大高度
return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
}
}实现平衡树的函数:
function balance(node) {
if (node == null) {
return node;
}
// 左子树高度比右子树高度大1以上
if (getAvlTreeHeight(node.left) - getAvlTreeHeight(node.right) > 1) {
if (getAvlTreeHeight(node.left.left) >= getAvlTreeHeight(node.left.right)) {
// 如果左子树的左子树高度大于等于左子树的右子树高度
// 直接进行右单旋
node = roateRight(node);
} else {
// 否则需要右-左双旋
node = roateRightLeft(node);
}
// 右子树高度比左子树高度大1以上
} else if (getAvlTreeHeight(node.right) - getAvlTreeHeight(node.left) > 1) {
if (getAvlTreeHeight(node.right.right) >= getAvlTreeHeight(node.right.left)) {
// 如果右子树的右子树高度大于等于右子树的左子树高度
// 直接进行左单旋
node = roateLeft(node);
} else {
// 否则需要左-右双旋
node = roateLeftRight(node);
}
}
return node;
}在二叉搜索树的基础上,每次插入节点,都需要做一次树的平衡处理:
var insertNode = function(node, newNode){
if (newNode.key < node.key){
if (node.left === null){
node.left = newNode;
// 插入节点后,做树的平衡处理
node.left = balance(node.left);
} else {
insertNode(node.left, newNode);
}
} else {
if (node.right === null){
node.right = newNode;
// 插入节点后,做树的平衡处理
node.right = balance(node.right);
} else {
insertNode(node.right, newNode);
}
}
}综上,一颗自平衡AVL树的原理及实现就完成了。