时间复杂度最小的最短路径算法?由这个想到的
最近看书发现了一段很有意思的东西,好像是谷歌的工程师发表在谷歌黑板报里的:
有一次,我笨得忘记了该如何在一个复杂的有向图中找出两点之间的最短路径。身边的一位工程师很郑重地告诉我说:“你知道吗?解决这个问题有两种方法,聪明人的方法和笨人的方法。聪明人的方法是:照着算法教科书的讲解,实现那个时间复杂度相当大的名叫嘀嘀哒嘀哒的最短路径算法。笨人的方法时间复杂度最低:找一堆线头来,按照有向图的结构连成一张网,然后一手拿一个顶点,向两边一抻,中间拉直了的那条路就是最短路径呀。”
“哇噻!笨是一种多么伟大的品格呀!”我眩晕得说不出话来。于是,我们这两个自认为足够笨的工程师足足花了两周的时间,用计算机程序模拟了不同材质的细线在北半球的重力条件下相互连接并在两个反方向作用力的影响下向两
边伸展的整个物理过程,然后以此为基础实现了时间复杂度最小的最短路径算法。——瞧,在 Google,什么东西都可以自己动手实现,什么东西也都可以推陈出新,我们的杰出表现就是最好的证明。
乍一看让人觉得甚是巧妙,不过总觉得有什么不对的地方,思索一番,是有此文
当然这个场景有个前提,边都是无向边,否则就不好模拟了。
我们来考虑一下这样一个模拟程序应该怎么写,就忽略什么细线的材质和北半球的重力条件了,先试着简化一下场景,因为我们想求源点S和目标点T之间的最短距离,只需要把源点S钉在墙上,其他点都挂在S下面,假设点不占空间,此时受重力作用,S和T的距离就是它们的最短距离了,这个问题应该是和原问题等价的,拉伸方向不同而已。
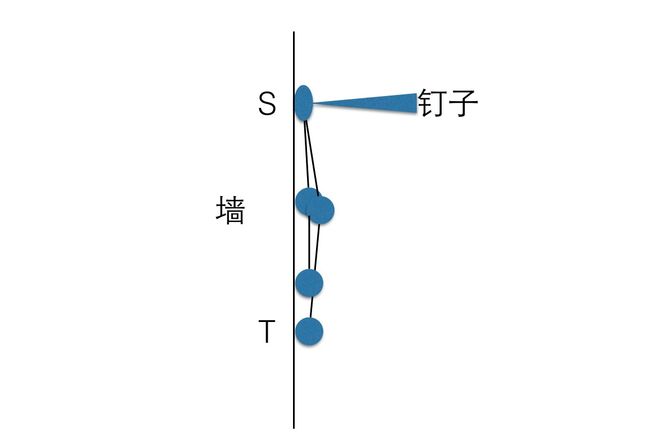
贪心模拟
这个东西怎么模拟呢?一时没有头绪,我们就再简化一下问题,假设每条边的长度都为1,这些就简单了嘛:最后挂出来的效果肯定是分层的,和S距离为1的点在第一层,和S距离为2的点在第二层:我们先把直接和S相连的点捋直了挂在下面,这些点肯定就是最短距离了,这是第一层;然后把能连到第一层并且还没挂上去的点挂到第二层,最后挂到T的时候结果就出来了。
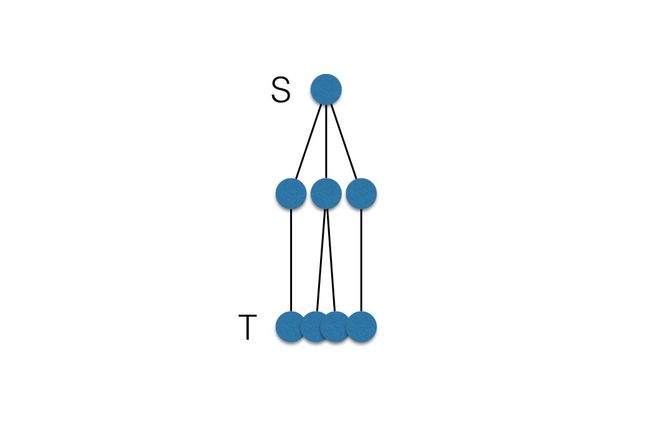
其实很清楚了,这不过就是简单的宽搜(BFS)而已,忽略掉同层相连的边之后整个图就简化为了一个树,树的根就是S,最短距离就是T点的深度,算法时间复杂度是O(M+N)的,M为边的数量,N为点的数量。
目前还不错,目前已知的最优两点间最短路径算法是O(M + N log N)的,可是别忘了我们现在是在特殊条件下:每条边的长度都是相同的。
如果边的长度各有不同,会出现什么情况呢?别的先不管,我们照例挂上第一层的点(左1):
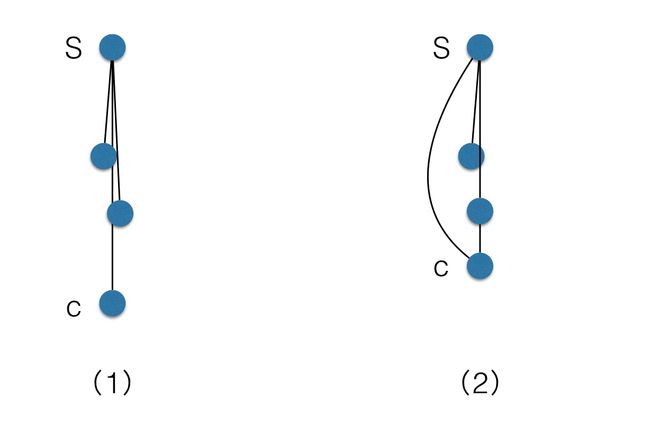
嗯,有问题了,这些点能拉直挂着的前提条件是此时它到源点的距离已经是最短的,所以当边的长度不定的时候,点和点直接相连的边不一定是最短距离!以上图的C点为例,通过一个中间节点挂上去的才是最短距离!(右2)
好像我们的方法用不上了,看看能不能改进解决呢?嗯,我们是要保证挂上去的就是最短距离,其实很好办嘛,我们一次只挂一个上去!
首先把直接连到S点且最近的那个点(假设是a)挂上去,此时肯定是最短距离;然后我们来挂第二个点,会有两种情况:1.这个点是直接挂在S上的;2.这个点是挂在a上的。此时我们就有了这两个候选集合,只需要选出其中到源点距离最短的点挂上即可(这个距离如果是和S连直接就是边长度,如果是和a连的就加上a到S的距离,假设我们选到了b),然后在下一步需要从三个候选集合(和S连的,和a连的,和b连的)里选择……
这样就满足了我们要求的前提条件,伪代码如下:
f = {}; 表示节点到边的最短距离
now = s;
f[s] = 0;
while (now!=t):
now <- 目前离S最近的点,通过筛选候选集合选出
f[now] = f[q] + e[q][now]; //假设now通过q连到源点S
嗯,搞定收工!算算复杂度,找距离最小的点可以用小根堆,老师教过,这是O(log n)的,外面还有个N层循环,还需要扫描边…………等等,话说这个描述咋这么眼熟啊?这不就是Dijkstra算法吗~~ ಥ_ಥ ~~,所以不管怎么玩,这个算法的复杂度最好就是O(m + n log n)的。
真模拟
看来这样类似贪心的模拟没用了啊,不得不上真家伙了,真实模拟一个网络来钉一次墙!
嗯,主要是靠脑暴,真要写一个就太麻烦了,我们回到原始的问题,也就是把网络平着抻直的场景:
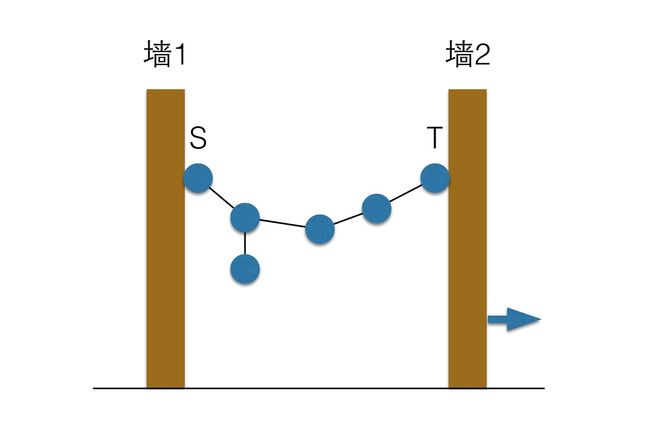
为了模拟拉这个动作,我们把S固定在墙1上,T固定在墙2上,然后一点一点把墙2从墙1的位置开始往右边挪动……
1.要真模拟,那么线和点都变成了实体,但它们都是没有碰撞体积的。
2.所谓模拟,其实就是按时间步去模拟,根据实体的受力情况改变它的位置,毕竟计算机的世界是离散的嘛,我们需要一点点改变点的未知以保证线不被拉断(为了防止线被拉断,当线被拉直的时候会产生拉力,这就是力的传递)。
3.所以每个时间步需要去扫描每个节点,力的来源一个是重力,一个是线的拉力,因此你还需要访问到所有的线,这里的复杂度已经到了O(M+N)。
4.最后我们要确定的其实就是整个系统稳定下来(挂稳不乱晃悠了)需要的时间步应该是多少。
因为我们的模拟是每次去扫描节点,但其实节点是不知道整个系统的真实情况的,比如我移动了一下墙2,所有的信息(力)都需要从T点传递过来:首先是T的邻点感知到了T位置的变化,因此产生了力的变化,这些点会受拉力移动一下,然后传播下一层的点再感知到这个变化,再根据受力情况改变自己的状态……and so on.
所以这个时间步其实是和树的深度(就是我们假模拟一开始用的那个东西)有关的!力的传递是需要时间的!所以时间步的复杂度其实是O(N),ps:真实世界的情况~~zhihu.com 力的传递有速度吗?
所以这个模拟方法的复杂度应该是O((M+N)*N)的,并不是所谓的时间复杂度最小的最短路径算法
后记
嗯,以上纯粹是我的推论~~~
因为也没实际看到原作者的实现,但我认为从理论上来说所谓模拟方法的复杂度肯定不可能低于目前已知最优算法的,所以工程狮还是自high居多,虽然看起来是很有说服力。
以上文章有问题还请指出,这个话题讨论起来我觉得还是蛮有意思的