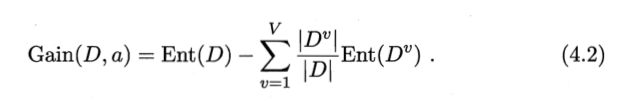决策树算法实现（以ID3为例）

决策树之训练过程在于建树，树结构的建立过程是递归的，关键步骤是选择属性进行划分数据集，选择划分的策略引出了各种版本决策树，ID3、C4.5和CART，其中前两种基于信息论，CART采用GINI系数对属性进行划分。编写决策树之前首先需要明确决策树的结构特点：

1、叶子节点是样本（用这类样本计算标签值，回归树用这个单元中的样本计算输出值，然后联合多个单元中的输出值和权重计算总的回归值）

2、非叶节点是数据集的属性名称，回归树里是该属性判断条件（特征名称或features）

3、所有属性的值是树枝，回归树里树枝是判断条件是否成立的yes或no

需要明了的是我们并不需要树来保存数据集，只需要保存数据集的属性名称和每个属性的值，最终得出标签即可。因此若要分析树的复杂度，应该是和属性及属性值的多少有关的。

（周志华老师西瓜书73页）

通过递归，不断的选择属性通过属性的值将数据集划分为不同的子集。（编写算法的时候头脑中要有清晰的手动切分数据集的映像才行），整个算法伪代码其实就是要编写的递归主函数。周志华老师西瓜书75页算法：

ID3算法为例（其他算法也一样，只是选择标签的函数要改写）：

既然该算法是个递归，首先要考虑的是定义递归出口，然后递归调用划分子数据集。这里我们采用简单的字典作为树结构的表示方式，因此遇到子节点时无需真正的标记是哪一类结点，而是在对应嵌套字典结构中输出就行。用其他树结构存放是需要另行树的表示，并标记类别标签。

1、当子数据集中只剩下一种标签时（即所属类别是一类），不再往下分（递归出口1），标记该叶子节点为该类标签即可

2、当划分完所有特征后还存在标签不同的样本（递归出口2），即属性集为空了还是分不出，或者样本集合已为空（图4.2第5步）

3、选择划分属性，对选择的每一个属性值递归切分子数据集

选择属性的子过程由信息增益决定，公式如下:

ID3算法训练过程代码及注释如下：

import math
import operator
def createDataSet():#模拟一个数据集
    dataset=[[1,1,'yes'],[1, 1, 'yes' ],
               [1, 0, 'no'],
               [0, 1, 'no'],
               [0, 1, 'no']]
    labels=['no surfacing','flippers']#表示属性名，而不是类别标签
    return dataset,labels

def calcShannonEnt(dataset):#按照西瓜书p75页公式计算香农熵值
    numEntries=len(dataset)
    labelCounts={}
    for featVec in dataset:#统计每个标签出现的次数，用于计算每类样本的比例
        currentLabel=featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel]=0
        labelCounts[currentLabel]+=1
    shannonEnt=0.0
    for key in labelCounts:
        prob=float(labelCounts[key])/numEntries  #该类标签出现的频数除以总样本数
        shannonEnt-=prob*math.log(prob,2) #p75页公式
    return shannonEnt

def splitDataSet(dataSet,axis,value):#返回按照axis属性切分，该属性的值为value的子数据集，并把该属性及其值去掉
    retDataSet=[]
    for featVec in dataSet:
        if featVec[axis]==value:#只把该属性上值是value的，加入到子数据集中
            reducedFeatVec=featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet
def chooseBestFeatureToSplit(dataSet):  #选择出用于切分的标签的索引值
    numberFeatures = len(dataSet[0])-1  #计算标签数量
    baseEntropy = calcShannonEnt(dataSet)#初始香农熵
    bestInfoGain = 0.0#初始增益0
    bestFeature = -1#最初标签索引
    for i in range(numberFeatures): #按信息增益选择标签索引
        featList = [example[i] for example in dataSet]#取出所有样本的第i个标签值
        uniqueVals = set(featList)#将标签值列表转为集合
        newEntropy =0.0
        for value in uniqueVals:  #对于一个属性i，对每个值切分成的子数据集计算其信息熵，将其加和就是总的熵
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy#计算信息增益
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

def majorityCnt(classList):#计算出现次数最多的标签，并返回该标签值
    classCount ={}
    for vote in classList:#投票法统计每个标签出现多少次
        if vote not in classCount.keys():
            classCount[vote]=0
        classCount[vote]+=1
    #print(classCount.items())
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)#对标签字典按值从大到小排序
    #print(sortedClassCount)
    return sortedClassCount[0][0]#取已拍序的dic_items的第一个item的第一个值

def createTree(dataSet, labels):
    #取出标签,生成列表
    classList=[example[-1] for example in dataSet]
    #如果D中样本属于同一类别，则将node标记为该类叶节点
    if classList.count(classList[0])==len(classList):
        return classList[0]
    #如果属性集为空或者D中样本在属性集上取值相同（意思是处理完所有特征后，标签还不唯一），
    #将node标记为叶节点，类比为样本数量最多的类,这里采用字典做树结构，所以叶节点直接返回标签就行
    if len(dataSet[0])==1:#此时存在所有特征相同但标签不同的数据，需要取数量最多标签的作为叶子节点，数据集包含了标签，所以是1
        return majorityCnt(classList)#这种情况西瓜书中的属性集为空和样本集为空的情况

    bestFeat=chooseBestFeatureToSplit(dataSet)#选择最佳标签进行切分，返回标签索引
    bestFeatLabel=labels[bestFeat] #根据最佳标签索引取出该属性名
    myTree={bestFeatLabel:{}} #定义嵌套的字典存放树结构
    del(labels[bestFeat])  #属性名称列表中删除已选的属性名
    featVals=[example[bestFeat] for example in dataSet]#取出所有样本的最优属性的值
    uniqueVals=set(featVals) #将属性值转成集合，值唯一
    for value in uniqueVals: #对每个属性值继续递归切分剩下的样本
        subLabels=labels[:]
        myTree[bestFeatLabel][value]=createTree(\
                splitDataSet(dataSet,bestFeat,value) ,
                subLabels)
    return myTree

if __name__=="__main__":
    dataSet,labels=createDataSet()
    dic=createTree(dataSet,labels)
    print(dic)

本文整理自西瓜书和CSDN博客 https://blog.csdn.net/flying_sfeng/article/details/62424225