约束最优化问题求解:拉格朗日乘子法和KKT条件
在约束最优化问题中,常常利用拉格朗日对偶性(Lagrange duality)将原始问题转换为对偶问题,通过解对偶问题而得到原始问题的解。该方法应用在许多统计学习方法中,例如最大熵模型和支持向量机。
对于等式约束的优化问题,可以应用拉格朗日乘子法(Lagrange Multiplier)去求取最优值;如果含有不等式约束,可以应用KKT(Karush-Kuhn-Tucker)条件去求取。当然,这两个方法求得的结果只是必要条件,只有当是凸函数的情况下,才能保证是充分必要条件。
1. 拉格朗日乘子法和KKT条件
通常我们需要求解的最优化问题有如下几类:
无约束优化问题,可以写为:
minf(x);有等式约束的优化问题,可以写为:
minf(x),s.t.hi(x)=0;i=1,...,n有不等式约束的优化问题,可以写为:
对于无约束优化问题,常常使用的方法就是Fermat定理,即使用求取 f(x) 的导数,然后令其为零,可以求得候选最优值,再在这些候选值中验证;如果是凸函数,可以保证是最优解。
对于有等式约束的优化问题,常常使用的方法就是拉格朗日乘子法,即把等式约束 hi(x) 用一个系数与 f(x) 写为一个式子,称为拉格朗日函数,而系数称为拉格朗日乘子。通过拉格朗日函数对各个变量求导,令其为零,可以求得候选值集合,然后验证求得最优值。
对于有不等式约束的优化问题,常常使用的方法就是KKT条件。同样地,我们把所有的等式、不等式约束与 f(x) 写为一个式子,也叫拉格朗日函数,系数也称拉格朗日乘子,通过一些条件,可以求出最优值的必要条件,这个条件称为KKT条件。
1.1 拉格朗日乘子法
对于等式约束,我们可以通过一个拉格朗日系数 a 把等式约束和目标函数组合成为一个式子 L(a,x)=f(x)+a⋅h(x) , 这里把 a 和 h(x) 视为向量形式, a 是横向量, h(x) 为列向量。
然后求取最优值,可以通过对 L(a,x) 对各个参数求导取零,联立等式进行求取。
1.2 KKT条件
对于含有不等式约束的优化问题,将其转化为对偶问题:
其中 L(a,b,x) 为由所有的不等式约束、等式约束和目标函数全部写成的一个式子 L(a,b,x)=f(x)+a⋅g(x)+b⋅h(x) ,KKT条件是说原始问题最优值 x∗ 和对偶问题最优值 a∗,b∗ 必须满足以下条件:
- ∇xL(a∗,b∗,x∗)=0,∇aL(a∗,b∗,x∗)=0,∇bL(a∗,b∗,x∗)=0 ;
- a∗⋅gi(x∗)=0 ;
- gi(x∗)≤0 ;
- a∗i≥0 , hj(x)=0 .
当原始问题的解和对偶问题的解满足KKT条件,并且 f(x),gi(x) 是凸函数时,原始问题的解与对偶问题的解相等。
求取这几个等式之后就能得到候选最优值。其中第2个式子非常有趣,因为 gi(x∗)≤0 ,如果要满足这个等式,必须 a∗=0 或者 gi(x∗)=0 . 这是SVM的很多重要性质的来源,如支持向量的概念。
2. 为什么拉格朗日乘子法和KKT条件能够得到最优值?
2.1 拉格朗日乘子法
设想我们想要最大化目标函数 f(x,y) 。可以投影在 x,y 构成的平面(曲面)上,即成为等高线;假设我们的约束 g(x,y)=0 ,在 x,y 构成的平面或者曲面上是一条曲线,如下图。
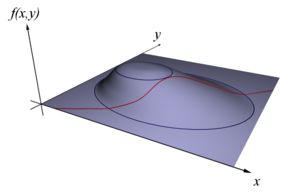

图片来自维基百科
假设 g(x,y) 与等高线相交,交点就是同时满足等式约束条件和目标函数的可行域的值,但肯定不是最优值,因为相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部,使得新的等高线与目标函数的交点的值更大或者更小,只有到等高线与目标函数的曲线相切的时候,才能取得最优值,即等高线和目标函数的曲线在该点的法向量必须有相同方向。
所以最优值必须满足: ∇f(x)=∇a⋅g(x) ,a是常数,表示左右两边同向,这个等式就是 L(a,x) 对参数求导的结果。
2.2 KKT条件
我们的目标问题是 minf(x) 。可以构造函数 L(a,b,x) :
此时 f(x) 与 maxa,bL(a,b,x) 是等价的。因为 h(x)=0,g(x)≤0,a⋅g(x)≤0 ,所以只有在 a⋅g(x)=0 的情况下 L(a,b,x) 才能取得最大值,这就是KKT的第二个条件。
因此我们的目标函数可以写为 minxmaxa,bL(a,b,x) 。如果用对偶表达式: maxa,bminxL(a,b,x) ,由于我们的优化是满足强对偶的(强对偶就是说对偶式子的最优值是等于原问题的最优值的),所以在取得最优值 x∗ 的条件下,它满足 f(x∗)=maxa,bminxL(a,b,x)=minxmaxa,bL(a,b,x)=f(x∗) ,我们来看看中间两个式子发生了什么事情:
可以看到上式本质上是说 minx(f(x)+a⋅g(x)+b⋅h(x)) 在 x∗ 取得了最小值,用fermat定理,即是说对于函数 f(x)+a⋅g(x)+b⋅h(x) ,求取导数要等于零,即
这就是KKT条件中第一个条件: ∇xL(a,b,x)=0 。
所有上述说明,满足强对偶条件的优化问题的最优值都必须满足KKT条件。可以把KKT条件视为是拉格朗日乘子法的泛化。
参考资料:
1. 深入理解拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
2. 李航,著. 统计学习方法[M]. 清华大学出版社,2012