逻辑回归--sklearn基本使用

逻辑回归–sklearn基本使用

penalty : str, ‘l1’ or ‘l2’, default: ‘l2’
惩罚项l1或者l2 l1可以使weight稀疏，l2可以使weight均衡，当solvers 为newton-cg’, ‘sag’ and ‘lbfgs’时，只可以是l2
C : float, default: 1.0
正则化的强度
fit_intercept : bool, default: True
默认为true，此参数为截距，即y=ax+b的b
intercept_scaling : float, default 1.
Useful only when the solver ‘liblinear’ is used and self.fit_intercept is set to True. In this case, x becomes [x, self.intercept_scaling], i.e. a “synthetic” feature with constant value equal to intercept_scaling is appended to the instance vector. The intercept becomes intercept_scaling * synthetic_feature_weight.
Note! the synthetic feature weight is subject to l1/l2 regularization as all other features. To lessen the effect of regularization on synthetic feature weight (and therefore on the intercept) intercept_scaling has to be increased.
class_weight : dict or ‘balanced’, default: None
默认是balanced，即{0：1，1：1}， 如果label中0比较重要，我就可以{0：2，1：1}，即代价敏感学习，一般在样本不平衡中使用

solver : {‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’}, default: ‘liblinear’
优化的算法
数据比较少时，用liblinear是一个比较好的选择。在数据比较多的情况下，sag更快一些
对于多分类问题，only ‘newton-cg’, and ‘lbfgs’ 可以处理multinomial loss， ‘liblinear’只可以解决ovr
‘newton-cg’, ‘lbfgs’ and ‘sag’ 只可以解决l2范式

multi_class : str, {‘ovr’, ‘multinomial’}, default: ‘ovr’
If the option chosen is ‘ovr’, then a binary problem is fit for each label. Else the loss minimised is the multinomial loss fit across the entire probability distribution. Works only for the ‘newton-cg’, ‘sag’ and ‘lbfgs’ solver.

n_jobs : int, default: 1
默认是1，此参数为线程数，可以根据个人电脑增加

Attributes

coef_ : array, shape (n_classes, n_features)
每一维特征的系数，即weight
intercept_ : array, shape (n_classes,)
截距，即bias

# -*- coding: utf-8 -*-
"""
Created on Wed Apr 12 21:28:40 2017

@author: 大帆
"""

from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif'] = ['SimHei']   
plt.rcParams['font.family']='sans-serif' 
plt.rcParams['axes.unicode_minus'] = False

iris=load_iris()
iris_data=iris.data
iris_target=iris.target

print(iris_data.shape)

pca=PCA(n_components=2)

X=pca.fit_transform(iris_data)
print(X.shape)

f=plt.figure()
ax=f.add_subplot(111)
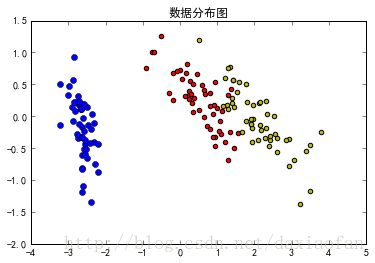
ax.plot(X[:,0][iris_target==0],X[:,1][iris_target==0],'bo')
ax.scatter(X[:,0][iris_target==1],X[:,1][iris_target==1],c='r')
ax.scatter(X[:,0][iris_target==2],X[:,1][iris_target==2],c='y')
ax.set_title('数据分布图')
plt.show()

clf=LogisticRegression(multi_class='ovr',solver='lbfgs',class_weight={0:1,1:1,2:1})
clf.fit(X,iris_target)
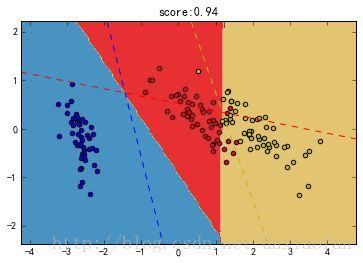
score=clf.score(X,iris_target)

x0min,x0max=X[:,0].min(),X[:,0].max()
x1min,x1max=X[:,1].min(),X[:,1].max()
h=0.05
xx,yy=np.meshgrid(np.arange(x0min-1,x0max+1,h),np.arange(x1min-1,x1max+1,h))
x_=xx.reshape([xx.shape[0]*xx.shape[1],1])
y_=yy.reshape([yy.shape[0]*yy.shape[1],1])
test_x=np.c_[x_,y_]

test_predict=clf.predict(test_x)
z=test_predict.reshape(xx.shape)
plt.contourf(xx,yy,z, cmap=plt.cm.Paired)
plt.axis('tight')
colors='bry'
for i,color in zip(clf.classes_,colors):
    idx=np.where(iris_target==i)
    plt.scatter(X[idx,0],X[idx,1],c=color,cmap=plt.cm.Paired)

xmin,xmax=plt.xlim()
coef=clf.coef_
intercept=clf.intercept_
def line(c,x0):
    return (-coef[c,0]*x0-intercept[c])/coef[c,1]
for i,color in zip(clf.classes_,colors):
    plt.plot([xmin,xmax],[line(i,xmin),line(i,xmax)],color=color,linestyle='--')
plt.title("score:{0}".format(score))

请看下一篇用tensorflow模拟逻辑回归http://blog.csdn.net/daxiaofan/article/details/70156357

参考：
sklearn–逻辑回归
(http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression)