python实现的 AWGN信道下QPSK调制信号的平均相位估计

AWGN信道下QPSK调制信号的平均相位估计

piccolo.用python简单实现的作业

Q1:在Eb/N0（5db~30db，间隔5db）下的加性高斯白噪声，并且假设信道为AWGN信道引入了30度的相位误差，采用QPSK调制信号作为导频信号，试仿真不同情况下的平均相位估计与采样点间曲线。

具体实现

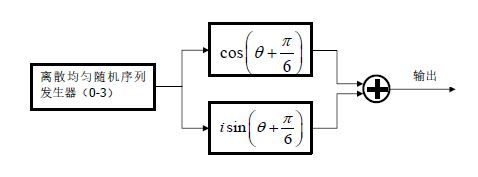
1.QPSK调制的实现

在这里便于仿真实现，采用相位选择法实现QPSK调制

• step0：生成0-3离散均匀随机序列
• step1：根据相位选择对应关系 实现相位映射
  
• step2：根据相位实现调制
  

2.AWGN信道下的实现

awgn相对容易实现，主要注意awgn信道 Eb/N0与SNR的转换

主要过程：

• QPSK信号过AWGN信道
• 信号采样并计算相位
• 解除相位偏置并计算误差以及误差的标准差作为误差估计

step0:生成0-3离散均匀随机序列 仿真实现带偏置的QPSK调制

import numpy as np 
from math import pi 
import matplotlib.pyplot as plt
import matplotlib
import scipy.signal as signal 
import math
import matplotlib.pyplot as plt
%matplotlib inline

#码元数
size = 1000
#扩展次数num 采样点数序列2 4 6...40
num = 40
samplenum=np.arange(2,40+2,2)
#信噪比序列5 10 15 ...30
SNR=np.arange(5,31,5)
#生成0-3离散均匀随机序列&定义相位偏移
a = np.random.randint(0, 4, size)
offset_phase=pi/6
#信噪比误差矩阵
wtf=np.zeros((6,20))
#相位选择向量
phase_map=([5*pi/4,7*pi/4,1*pi/4,3*pi/4])

phase=np.zeros(size)
data=np.zeros(size)
for i in range(size):
   t=a[i]
   phase[i]=phase_map[t]
   
#加相位偏置    
phase1=phase+np.ones(size)*offset_phase;
#data&phase
data=np.cos(phase1)+1j*np.sin(phase1)
phase=phase*180/pi;

step1:定义函数体 信号的扩展函数、AWGN信道函数、采样函数、求取采样点角度函数、计算平均相位估计误差函数

#一些函数
#扩展函数 扩展num次
def spread(data,num):
   tran_data=[]
   for k in range(size):
      tran_data.extend(np.ones(num)*data[k])
   return tran_data  

# 定义加性高斯白噪声 函数
def awgn(y, snr):
   snr1 = 10 ** (snr / 10.0)
   xpower = np.sum(y ** 2) / len(y)
   npower = xpower / snr1
   return np.random.randn(len(y)) * np.sqrt(npower) + y

#采样函数 
def sampling(single,sample_num):
   SAMPLE=[]
   for k in range(size):
       temp=np.round(np.linspace(k*num,(k+1)*num-1,sample_num))
       temp1=temp.tolist()
       for m in range(len(temp1)):
           temp1[m]=int(temp1[m])
       SAMPLE.append(np.sum(noise_qpsk[temp1])/sample_num)
   return SAMPLE

#求取采样点相位
def arg(SAMPLE):
   r1=np.real(SAMPLE)
   r2=np.imag(SAMPLE)
   arg=[]
   for k in range(size):
       t=(math.atan(abs(r2[k]/r1[k])))*180/math.pi
       if r1[k]>0:
           if r2[k]>0:
               arg.append(t)
           else:
               arg.append(-t)
       else:
           if r2[k]>0:
               arg.append(180-t)
           else:
               arg.append(t-180)    
       #arg.append(math.acos(r1[k]/(np.sqrt(r2[k]**2+r1[k]**2)))*180/math.pi)        
   return arg
#采样点相位偏差
def argerror(arg,phase1):
   ermat=[]
   for k in range(len(arg)):
       if arg[k]<0:
           arg[k]=arg[k]+360
       ermat.append(arg[k]-phase1[k])
       if abs(ermat[k])>180:
           if ermat[k]>180:
               ermat[k]=ermat[k]-360
           else:
               ermat[k]=ermat[k]+360
   error=np.array(ermat)-30
   return error

step2:开始进行不同Eb/N0、不同采样点下的仿真计算

#先对序列num次扩展 便于后面采样
data1=spread(data,num)
tran_data1=np.array(data1)
k=0
while k<6:
   snr=SNR[k]
   #过AWGN信道
   noise_qpsk = awgn(tran_data1, snr)
   for m in range(20):
       sample_num=samplenum[m]
       #进行采样
       SAMPLE=sampling(noise_qpsk, sample_num)
       #采样点 求解相位
       sample_arg=arg(SAMPLE)
       #采样点相位误差
       sample_error=argerror(sample_arg,phase)
       
       wtf[k][m]=np.sqrt(np.sum(sample_error**2)/size)
   k+=1

step3:绘图&分析

from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题

x = samplenum 
#面向对象的绘图方式
fig,ax = plt.subplots() 
ax.figsize=(48,24)
plt.rcParams['image.interpolation'] = 'nearest' # 设置 interpolation style
plt.rcParams['image.cmap'] = 'gray' # 设置 颜色 style
plt.rcParams['savefig.dpi'] = 300 #图片像素
plt.rcParams['figure.dpi'] = 300 #分辨率
plt.rcParams['figure.figsize'] = (8.0, 4.0)
ins0=ax.plot(x,wtf[0], label = 'Eb/N0=5dB')
ins1=ax.plot(x,wtf[1], label = 'Eb/N0=10dB')
ins2=ax.plot(x,wtf[2], label = 'Eb/N0=15dB')
ins3=ax.plot(x,wtf[3], label = 'Eb/N0=20dB')
ins4=ax.plot(x,wtf[4], label = 'Eb/N0=25dB')
ins5=ax.plot(x,wtf[5], label = 'Eb/N0=30dB')
lns = ins0+ins1+ins2+ins3+ins4+ins5
labs = [l.get_label() for l in lns]
ax.legend(lns, labs, loc=0)
ax.set_xlabel("采样点") 
ax.set_ylabel("平均相位估计误差") 
ax.set_title("Q1：AWGN信道") 
ax.set_xticks(x)
ax.grid()
plt.savefig('0.png')

最后结果：

此处用标准差做平均相位估计误差。

根据图中的曲线结果可知，在同一Eb/N0条件下，误差估计偏离程度随着采样率的增加而降低。在同一采样率的下，误差估计偏离程度随着Eb/N0的增加而降低。曲线的趋势符合理论表现。