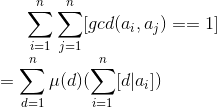首师大附中集训第九天专题测试
正题
第一题:有 n 个数字,a[1],a[2],…,a[n]。有一个集合,刚开始集合为空。然后有一种操作每次向 集合中加入一个数字或者删除一个数字。每次操作给出一个下标 x(1 ≤ x ≤ n),如果 a[x]已 经在集合中,那么就删除 a[x],否则就加入 a[x]。 问每次操作之后集合中互质的数字有多少对。 注意,集合中可以有重复的数字,两个数字不同当且仅当他们的下标不同。 比如 a[1]=a[2]=1。那么经过两次操作 1,2 之后,集合之后存在两个 1,有一对互质。
把答案式子写出来,直接莫比乌斯反演即可:
然后发现第二个sigma其实是可以支持动态维护的,时间复杂度![]()
#include
#include
#include
#include
using namespace std;
int n,q;
int data=0,x,temp;
int a[100010];
int mu[500010],p[500010],g[500010];
bool vis[500010],tf[500010],we[500010];
long long ans=0;
void del(int x){
for(int i=1;i*i<=x;i++) if(x%i==0){
temp=x/i;
if(we[i]){
g[i]--;
ans-=(1ll*(g[i]+1)*(g[i]+1)-1ll*g[i]*g[i])*mu[i];
}
if(we[temp] && temp!=i){
g[temp]--;
ans-=(1ll*(g[temp]+1)*(g[temp]+1)-1ll*g[temp]*g[temp])*mu[temp];
}
}
if(x==1) ans++;
}
void ins(int x){
for(int i=1;i*i<=x;i++) if(x%i==0){
temp=x/i;
if(we[i]){
ans+=(1ll*(g[i]+1)*(g[i]+1)-1ll*g[i]*g[i])*mu[i];
g[i]++;
}
if(we[temp] && temp!=i){
ans+=(1ll*(g[temp]+1)*(g[temp]+1)-1ll*g[temp]*g[temp])*mu[temp];
g[temp]++;
}
}
if(x==1) ans--;
}
int main(){
freopen("coprime.in","r",stdin);
freopen("coprime.out","w",stdout);
scanf("%d %d",&n,&q);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),data=max(data,a[i]);
mu[1]=1;we[1]=true;
for(int i=2;i<=data;i++){
if(!vis[i]) p[++p[0]]=i,mu[i]=-1;
for(int j=1;(temp=i*p[j])<=data;j++){
vis[temp]=true;
if(i%p[j]==0) break;
mu[temp]=-mu[i];
}
if(mu[i]!=0) we[i]=true;
}
while(q--){
scanf("%d",&x);
if(tf[x]) del(a[x]),tf[x]=false;
else ins(a[x]),tf[x]=true;
printf("%lld\n",ans/2);
}
} 第二题:这题没有部分分。
Fib(N)表示斐波那契数列的第 N 项(F(0) = 0, F(1) = 1),给出 N 和 K,求 Fib(N) mod Fib(K)。 由于结果太大,输出 Mod 1000000007 的结果。
发现很容易就可以入得了手。因为有![]()
不断递归就可以得到![]()
发现做不了两个数的乘法。但是我们有这一条公式:
具体可以看我的blog。
剩下的就是一个斐波那契的负数项。
怎么求,找规律发现![]() ,那么就可以做了。
,那么就可以做了。
不知道那条公式所以后面的都没做出来,推到第三行了发现没有部分分,然后就自闭了。
#include
#include
#include
#include
using namespace std;
int T;
long long n,k;
const long long mod=1e9+7;
long long p[2][2],op[2][2],temp[2][2];
long long ksm(long long x,long long t){
if(x==-1) return t&1?-1:1;
long long tot=1;
while(t){
if(t&1) (tot*=x)%=mod;
(x*=x)%=mod;
t/=2;
}
return tot;
}
long long F(long long x){
if(x<0) x=-x;
if(x==0) return 0;
if(x==1) return 1;
op[0][0]=op[1][1]=1;op[0][1]=op[1][0]=0;
p[0][0]=p[0][1]=p[1][0]=1;p[1][1]=0;x-=1;
while(x){
if(x&1) {
for(int i=0;i<2;i++) for(int j=0;j<2;j++) for(int k=0;k<2;k++)
(temp[i][j]+=op[i][k]*p[k][j]%mod)%=mod;
for(int i=0;i<2;i++) for(int j=0;j<2;j++) op[i][j]=temp[i][j],temp[i][j]=0;
}
for(int i=0;i<2;i++) for(int j=0;j<2;j++) for(int k=0;k<2;k++)
(temp[i][j]+=p[i][k]*p[k][j]%mod)%=mod;
for(int i=0;i<2;i++) for(int j=0;j<2;j++) p[i][j]=temp[i][j],temp[i][j]=0;
x/=2;
}
return (op[0][0]+mod)%mod;
}
int main(){
scanf("%d",&T);
while(T--){
scanf("%lld %lld",&n,&k);
long long x=n/k,y=n%k;
if(y==0) printf("%d\n",0);
else{
if(x%2==1) x++,y-=k;x/=2;
long long ans=ksm(-1,1ll*k*x)*(y<0?ksm(-1,-y-1):1);
if(ans==-1) ans=(F(k)+mod-F(y))%mod;
else ans=F(y);
printf("%lld\n",ans);
}
}
} 第三题:题面没有位置对称,所以我觉得不可做。直接跳了。
然后老师下午说题面出锅了,题目其实就是万径人踪灭。。。。
我就不补了,这题很早就写过了。