拉格朗日函数、对偶上升法、对偶分解法

拉格朗日函数

用于解决满足约束条件的最值问题
注意，该方法均只能保证求得的结果是必要条件。只有当原函数是凸函数时，才能保证求得的结果是充要条件

拉格朗日乘子法

适用于具有等式约束的最大值/最小值问题

minf(x)s.t.ormaxf(x)φi(x)=0,i=1,2,…,n}⇒{L(x,λ)=f(x)+∑ni=1λiφi(x)∇L(x,λ)=0(1) (1) min f ( x ) or max f ( x ) s.t. φ i ( x ) = 0 , i = 1 , 2 , … , n } ⇒ { L ( x , λ ) = f ( x ) + ∑ i = 1 n λ i φ i ( x ) ∇ L ( x , λ ) = 0

其中 L(x,λ) L ( x , λ ) 被称为拉格朗日函数，系数 λ λ 被称为拉格朗日乘子或者对偶变量。通过 ∇ ∇ 计算后，可得到候选集，然后从候选集中验算选择满足条件的结果即可。（ ∇ ∇ ：依次对函数所有自变量求偏导）

KKT条件

适用于同时具有等式约束和不等式约束的最小值问题

mins.t.f(x)φi(x)=0,i=1,2,…,nhj(x)≤0,j=1,2,…,m⎫⎭⎬⎪⎪⇒L(x,λ,ι)=f(x)+∑i=1nλiφi(x)+∑j=1mιjhj(x)(2) (2) min f ( x ) s.t. φ i ( x ) = 0 , i = 1 , 2 , … , n h j ( x ) ≤ 0 , j = 1 , 2 , … , m } ⇒ L ( x , λ , ι ) = f ( x ) + ∑ i = 1 n λ i φ i ( x ) + ∑ j = 1 m ι j h j ( x )

上述式子成立的 必要前提是KKT条件：

KKT s.t.L(x,λ,ι)对x求偏导存在λi(x)=0,i=1,2,…,nιjhj(x)=0,ιj≥0,j=1,2,…,m(3) (3) KKT s.t. L ( x , λ , ι ) 对 x 求 偏 导 存 在 λ i ( x ) = 0 , i = 1 , 2 , … , n ι j h j ( x ) = 0 , ι j ≥ 0 , j = 1 , 2 , … , m

其中 λ,ι λ , ι 被称为拉格朗日乘子或者对偶变量

下面直观地说下为什么会有第三个条件要成立
由于 ιj≥0,hj(x)≤0 ι j ≥ 0 , h j ( x ) ≤ 0 ，所以 ιjhj(x)≤0 ι j h j ( x ) ≤ 0 ；又因为 λi(x)=0 λ i ( x ) = 0 ，所以 L(x,λ,ι) L ( x , λ , ι ) 仅有在 ιjhj(x)=0 ι j h j ( x ) = 0 下才能取得最大值，故这是KKT第三个条件必须要成立的原因——即第三个条件满足时，它意味着有 maxL(x,λ,ι)=f(x) max L ( x , λ , ι ) = f ( x ) ，接下来就是求解 minf(x) min f ( x ) ，所以该过程又可记为： minf(x)=minxmaxλ,ιL(x,λ,ι) min f ( x ) = min x max λ , ι L ( x , λ , ι )

这种类型的约束最优解的解法，其实就是根据KKT的三个条件来求解，步骤如下：
【1】列出拉格朗日函数 L(x,λ,ι) L ( x , λ , ι )
【2】对该函数分别求 x、λ x 、 λ 的偏导函数并分别赋值为 0，获得偏导函数组
【3】枚举KKT条件三中 ιjhj(x)=0 ι j h j ( x ) = 0 的所有情况： ιj=0,hj(x)≤0 ι j = 0 , h j ( x ) ≤ 0 和 ιj>0,hj(x)=0 ι j > 0 , h j ( x ) = 0
【4】将【3】中的每种情况依次带入【2】中的偏导函数组中进行求解，查看是否有解
【5】将【4】中获得的所有候选解带入原函数，挑选最小结果的那个

例子：

mins.t(x−2)2+2(y−1)2x+4y−3≤0−x+y≤0 m i n ( x − 2 ) 2 + 2 ( y − 1 ) 2 s . t x + 4 y − 3 ≤ 0 − x + y ≤ 0

解：

[1][2][3][4][5]L(x,y,μ1,μ2)=(x−2)2+2(y−1)2+μ1(x+4y−3)+μ2(−x+y)∂L∂x=2(x−2)+μ1−μ2∂L∂y=4(y−1)−4μ1+μ2μ1(x+4y−3)=0μ2(−x+y)=0μ1,μ2≥0μ1=μ2=0→x=2,y=1μ1=0,−x+y=0→x=43,μ2=−43x+4y−3=0,μ2=0→x=53,y=13,μ1=23x+4y−3=0,x−y=0→x=35,y=frac35,μ1=2225,μ2=−4825x=53,y=13时，minf(x,y)=49 [ 1 ] L ( x , y , μ 1 , μ 2 ) = ( x − 2 ) 2 + 2 ( y − 1 ) 2 + μ 1 ( x + 4 y − 3 ) + μ 2 ( − x + y ) [ 2 ] ∂ L ∂ x = 2 ( x − 2 ) + μ 1 − μ 2 ∂ L ∂ y = 4 ( y − 1 ) − 4 μ 1 + μ 2 [ 3 ] μ 1 ( x + 4 y − 3 ) = 0 μ 2 ( − x + y ) = 0 μ 1 , μ 2 ≥ 0 [ 4 ] μ 1 = μ 2 = 0 → x = 2 , y = 1 μ 1 = 0 , − x + y = 0 → x = 4 3 , μ 2 = − 4 3 x + 4 y − 3 = 0 , μ 2 = 0 → x = 5 3 , y = 1 3 , μ 1 = 2 3 x + 4 y − 3 = 0 , x − y = 0 → x = 3 5 , y = f r a c 3 5 , μ 1 = 22 25 , μ 2 = − 48 25 [ 5 ] x = 5 3 , y = 1 3 时 ， min f ( x , y ) = 4 9

对偶上升法

前提知识：共轭函数、对偶函数、线性约束下对偶函数的共轭形式、对偶问题

共轭函数

原函数：f(x):Rn→R共轭函数：f∗(y):Rn→R}→f∗(y)=supx∈domf(yTx−f(x))(4) (4) 原 函 数 ： f ( x ) : R n → R 共 轭 函 数 ： f ∗ ( y ) : R n → R } → f ∗ ( y ) = sup x ∈ d o m f ( y T x − f ( x ) )

其中， sup(g(x)) sup ( g ( x ) ) 表示函数 g(x) g ( x ) 在整个定义域 x∈domg x ∈ d o m g 中的最大值， y y 则取任意常数 or 常向量。
这样，对每一个 y y 值， f∗(y) f ∗ ( y ) 都会对应一个值。将 y y 扩展到整个取值范围后，就可得到关于 y y 函数 f∗(y) f ∗ ( y ) ，即函数 f(x) f ( x ) 的共轭函数。（与下面的对偶函数类似，只不过一个是取最小，一个是取最大）

拉格朗日对偶函数

对于定义域 D 上 x x 的所有取值，拉格朗日函数的最小值即为拉格朗日对偶函数(dual function)：

g(λ,ι)=infx∈DL(x,λ,ι)(5) (5) g ( λ , ι ) = inf x ∈ D L ( x , λ , ι )

该式表示：将 x x 视为常数，则 L(x,λ,ι) L ( x , λ , ι ) 则是只关于自变量 λ,ι λ , ι 的函数。对整个定义域 D 内所有的 x x 值，都有与之对应的关于只关于自变量 λ,ι λ , ι 的函数，这些函数集合在整个自变量取值范围中的最小值，即为拉格朗日对偶函数 。如下图所示：

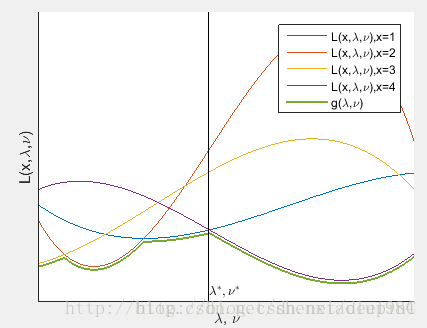
所以 g(λ,ι)=minL(x,λ,ι)≤minxmaxλ,ιL(x,λ,ι)=minf(x) g ( λ , ι ) = min L ( x , λ , ι ) ≤ min x max λ , ι L ( x , λ , ι ) = min f ( x ) 恒成立，即 拉格朗日对偶函数是最优解的下界

线性约束下拉格朗日函数对偶函数的共轭形式

考虑线性约束（即自变量的幂均为 1）下的最优化问题：

s.t.minf(x)Ax=a,Bx≤b min f ( x ) s . t . A x = a , B x ≤ b

其共轭形式求解如下

g(λ,ι)====infx∈DL(x,λ,ι)infx∈Df(x)+λ(Ax−a)+ι(Bx−b)−(λa+ιb)−supx∈D{(−λA−ιB)x−f(x)}−(λa+ιb)−f∗(−λA−ιB) g ( λ , ι ) = inf x ∈ D L ( x , λ , ι ) = inf x ∈ D f ( x ) + λ ( A x − a ) + ι ( B x − b ) = − ( λ a + ι b ) − sup x ∈ D { ( − λ A − ι B ) x − f ( x ) } = − ( λ a + ι b ) − f ∗ ( − λ A − ι B )

即

s.t.minf(x)Ax=a,Bx≤b}⇒g(λ,ι)=−(λa+ιb)−f∗(−λA−ιB)(6) (6) min f ( x ) s . t . A x = a , B x ≤ b } ⇒ g ( λ , ι ) = − ( λ a + ι b ) − f ∗ ( − λ A − ι B )

对偶问题

求解上述对偶函数的最大值，就是原优化问题的拉格朗日对偶问题(dual problem)：

maxg(λ,ι)s.t.λ,ι≥0(7) (7) max g ( λ , ι ) s . t . λ , ι ≥ 0

由于

g(λ,ι)=≤≤minL(x,λ,ι)minxmaxλ,ιL(x,λ,ι)maxλ,ιL(x,λ,ι)⎫⎭⎬⎪⎪⇒maxg(λ,ι)≤maxλ,ιL(x,λ,ι)(8) (8) g ( λ , ι ) = min L ( x , λ , ι ) ≤ min x max λ , ι L ( x , λ , ι ) ≤ max λ , ι L ( x , λ , ι ) } ⇒ max g ( λ , ι ) ≤ max λ , ι L ( x , λ , ι )

所以对偶问题的求解，即对偶函数的最优解，即为 maxλ,ιL(x,λ,ι) max λ , ι L ( x , λ , ι ) 的最优解（用于替代求解 maxλ,ιL(x,λ,ι) max λ , ι L ( x , λ , ι ) ，是其简化版）。
若 f(x) f ( x ) 复杂，而 g(λ,ι) g ( λ , ι ) 简单，则可通过下述步骤求解 minf(x) min f ( x ) 最优解：

1. 求解 maxg(λ,ι) max g ( λ , ι ) 得到 λ,ι λ , ι
2. 将 λ,ι λ , ι 代入 L(x,λ,ι) L ( x , λ , ι ) ，然后求解 minL(x,λ,ι) min L ( x , λ , ι ) 得到 x x
3. x x 即为 minf(x) min f ( x ) 最优解

注意，该过程实现了：将language乘子将带有约束的最小最大化问题转化为无约束的language函数求解

对偶上升法

关键：利用上述的求解 minf(x) min f ( x ) 最优解的步骤

对偶上升法处理步骤：

1. 假设 λk,ιk λ k , ι k 已经是对偶问题的最优解
2. 求解 minL(x,λk,ιk) min L ( x , λ k , ι k ) 得到 xk+1 x k + 1 ： xk+1=argminxL(x,λk,ιk) x k + 1 = arg ⁡ min x L ( x , λ k , ι k )
3. 显然，曲线 L(xk+1,λk,ιk) L ( x k + 1 , λ k , ι k ) 处于所有曲线中的最下面，根据上述对偶函数的定义可知： g(λk,ιk)=L(xk+1,λk,ιk) g ( λ k , ι k ) = L ( x k + 1 , λ k , ι k )
4. 利用梯度上升法更新对偶问题最优解：
   λk+1ιk+1====λk+α⋅∂g(λ,ι)∂λ|λ=λk,ι=ιkλk+α⋅∂L(x,λ,ι)∂λ|x=xk+1,λ=λk,ι=ιkιk+β⋅∂g(λ,ι)∂ι|λ=λk,ι=ιkιk+β⋅∂L(x,λ,ι)∂ι|x=xk+1,λ=λk,ι=ιk λ k + 1 = λ k + α ⋅ ∂ g ( λ , ι ) ∂ λ | λ = λ k , ι = ι k = λ k + α ⋅ ∂ L ( x , λ , ι ) ∂ λ | x = x k + 1 , λ = λ k , ι = ι k ι k + 1 = ι k + β ⋅ ∂ g ( λ , ι ) ∂ ι | λ = λ k , ι = ι k = ι k + β ⋅ ∂ L ( x , λ , ι ) ∂ ι | x = x k + 1 , λ = λ k , ι = ι k
5. 按 1~4 迭代进行

对偶分解法

假设目标函数是可分解的：

f(x)=∑ni=0fi(xi)s.t.Ax=b,其中x=(x0,x1,⋯,xn)T f ( x ) = ∑ i = 0 n f i ( x i ) s . t . A x = b , 其 中 x = ( x 0 , x 1 , ⋯ , x n ) T

则拉格朗日函数可分解，即：

L(x,λ)==∑ni=0L(xi,λ)∑ni=0fi(xi)+λAix−λbi L ( x , λ ) = ∑ i = 0 n L ( x i , λ ) = ∑ i = 0 n f i ( x i ) + λ A i x − λ b i

所以可以将对偶上升法中的第 2 步修改为： xk+1i=argminxiLi(xi,λk) x i k + 1 = arg ⁡ min x i L i ( x i , λ k )
即可并行计算 xk+1 x k + 1 的每个元素，从而快速得到 xk+1 x k + 1

参考链接
参考链接