FPGA学习笔记---CORDIC算法

 

参考资料：

 

https://blog.csdn.net/qq_39210023/article/details/77456031 （本篇的sin和cos程序可用，参考此篇写出我的actan）

 

https://blog.csdn.net/messi_cyc/article/details/77966457

 

https://wenku.baidu.com/view/6c623aa8910ef12d2bf9e732.html?sxts=1521614036184（Xilinx CORDIC，值得参考）

 

http://blog.sina.com.cn/s/blog_b906c1070102ve1l.html  （本篇的C语言程序很有参考价值）

 

 

CORDIC算法涉及3种坐标系、2种模式，共计6这个组合，其中在圆周坐标系下利用旋转模式实现sin和cos的文章和资料较多，其他5种较少，利用FPGA实现的更少。本文实现圆周坐标系下的向量模式，对输入的一对（x，y），求得actan（y/x）和 sqrt（x^2+y^2） ，具体原理以上资料均已很清楚，如有不清楚的可在评论区提出，文中不再赘述。文章侧重于Verilog程序的设计。 

（1）输入、输出位宽32，设为signed有符号数，这样便于下面的操作，通过判断y的最高位y[31]为1还是为0即可判断正负，对于移位操作也可以直接运用“>>>”，而不需要进行位拼接操作

 

 

//输入
input                       clk;
input                       rst_n;
input   signed    [31:0]    x;
input   signed    [31:0]    y;

//输出
output reg signed [31:0]    sqrt;
output reg signed [31:0]    actan;

 

（2）定义旋转角度常量和中间寄存器，此处借鉴了参考资料1中的定义（几乎是照抄，特别感谢@善良的一休君，文章给了我很多启发）

 

//以下为了避免浮点运算，对每个变量θi都放大了2^16倍
`define rot0  32'd2949120     //45度*2^16
`define rot1  32'd1740992     //26.5651度*2^16
`define rot2  32'd919872      //14.0362度*2^16
`define rot3  32'd466944      //7.1250度*2^16
`define rot4  32'd234368      //3.5763度*2^16
`define rot5  32'd117312      //1.7899度*2^16
`define rot6  32'd58688       //0.8952度*2^16
`define rot7  32'd29312       //0.4476度*2^16
`define rot8  32'd14656       //0.2238度*2^16
`define rot9  32'd7360        //0.1119度*2^16
`define rot10 32'd3648        //0.0560度*2^16
`define rot11 32'd1856        //0.0280度*2^16
`define rot12 32'd896         //0.0140度*2^16
`define rot13 32'd448         //0.0070度*2^16
`define rot14 32'd256         //0.0035度*2^16
`define rot15 32'd128         //0.0018度*2^16

//全部定义为有符号型数据
reg signed  [31:0]      x0=0,y0=0,z0=0;
reg signed  [31:0]      x1=0,y1=0,z1=0;
reg signed  [31:0]      x2=0,y2=0,z2=0;
reg signed  [31:0]      x3=0,y3=0,z3=0;
reg signed  [31:0]      x4=0,y4=0,z4=0;
reg signed  [31:0]      x5=0,y5=0,z5=0;
reg signed  [31:0]      x6=0,y6=0,z6=0;
reg signed  [31:0]      x7=0,y7=0,z7=0;
reg signed  [31:0]      x8=0,y8=0,z8=0;
reg signed  [31:0]      x9=0,y9=0,z9=0;
reg signed  [31:0]      x10=0,y10=0,z10=0;
reg signed  [31:0]      x11=0,y11=0,z11=0;
reg signed  [31:0]      x12=0,y12=0,z12=0;
reg signed  [31:0]      x13=0,y13=0,z13=0;
reg signed  [31:0]      x14=0,y14=0,z14=0;
reg signed  [31:0]      x15=0,y15=0,z15=0;
reg signed  [31:0]      x16=0,y16=0,z16=0;

reg signed  [31:0]      ppp;
reg signed  [31:0]      aaa;

（3）数据预处理，将输入数据x，y赋值给对应的x0，y0，而z0初值设为0，进行16级迭代，最后可得到z16=z0+actan(y/x)=actan(y/x)

//数据预处理
always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        x0 <= 1'b0;                         
        y0 <= 1'b0;
        z0 <= 1'b0;
    end
    else  begin
        x0 <= x;           //x0赋初值
        y0 <= y;				//y0赋初值0
        z0 <= 32'd0;			//z0赋初值0
    end
end

//第一级迭代
always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        x1 <= 1'b0;                         
        y1 <= 1'b0;
        z1 <= 1'b0;
    end
    else if( !y0[31] )  begin	//有符号数，最高位为符号位，是1表示<0
      x1 <= x0 + y0;
      y1 <= y0 - x0;
      z1 <= z0 + `rot0;
    end
    else  begin					//有符号数，最高位为符号位，是0表示>0
      x1 <= x0 - y0;
      y1 <= y0 + x0;
      z1 <= z0 - `rot0;
    end
end

always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        x2 <= 1'b0;                         
        y2 <= 1'b0;
        z2 <= 1'b0;
    end
    else if( !y1[31] )  begin		//有符号数，最高位为符号位，是1表示<0
        x2 <= x1 + (y1 >>> 1);	//右移1位,即/2,相当于*2^(-1),此时i = 1
        y2 <= y1 - (x1 >>> 1);	//右移1位,即/2,相当于*2^(-1)
        z2 <= z1 + `rot1;
   end
   else  begin
       x2 <= x1 - (y1 >>> 1);
       y2 <= y1 + (x1 >>> 1);
       z2 <= z1 - `rot1;
   end
end

always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        x3 <= 1'b0;                         
        y3 <= 1'b0;
        z3 <= 1'b0;
    end
    else if( !y2[31] )  begin			
       x3 <= x2 + (y2 >>> 2);		//右移2位,即/4,相当于*2^(-2),此时i = 2
       y3 <= y2 - (x2 >>> 2);
       z3 <= z2 + `rot2;
   end
   else  begin
       x3 <= x2 - (y2 >>> 2);
       y3 <= y2 + (x2 >>> 2);
       z3 <= z2 - `rot2;
   end
end

always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        x4 <= 1'b0;                         
        y4 <= 1'b0;
        z4 <= 1'b0;
    end
    else if( !y3[31] )  begin
       x4 <= x3 + (y3 >>> 3);		//右移3位,即/8,相当于*2^(-3),此时i = 3
       y4 <= y3 - (x3 >>> 3);
       z4 <= z3 + `rot3;
   end
   else  begin
       x4 <= x3 - (y3 >>> 3);
       y4 <= y3 + (x3 >>> 3);
       z4 <= z3 - `rot3;
   end
end

always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        x5 <= 1'b0;                         
        y5 <= 1'b0;
        z5 <= 1'b0;
    end
    else if( !y4[31] )  begin
       x5 <= x4 + (y4 >>> 4);		//右移4位,即/16,相当于*2^(-4),此时i = 4
       y5 <= y4 - (x4 >>> 4);
       z5 <= z4 + `rot4;
   end
   else  begin
       x5 <= x4 - (y4 >>> 4);
       y5 <= y4 + (x4 >>> 4);
       z5 <= z4 - `rot4;
   end
end

always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        x6 <= 1'b0;                         
        y6 <= 1'b0;
        z6 <= 1'b0;
    end
    else if( !y5[31] )  begin
       x6 <= x5 + (y5 >>> 5);
       y6 <= y5 - (x5 >>> 5);
       z6 <= z5 + `rot5;
   end
   else  begin
       x6 <= x5 - (y5 >>> 5);
       y6 <= y5 + (x5 >>> 5);
       z6 <= z5 - `rot5;
   end
end

always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )
    begin
        x7 <= 1'b0;                         
        y7 <= 1'b0;
        z7 <= 1'b0;
    end
    else if( !y6[31] )  begin
       x7 <= x6 + (y6 >>> 6);
       y7 <= y6 - (x6 >>> 6);
       z7 <= z6 + `rot6;
   end
   else  begin
       x7 <= x6 - (y6 >>> 6);
       y7 <= y6 + (x6 >>> 6);
       z7 <= z6 - `rot6;
   end
end

always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )
    begin
        x8 <= 1'b0;                         
        y8 <= 1'b0;
        z8 <= 1'b0;
    end
    else if( !y7[31] )  begin
       x8 <= x7 + (y7 >>> 7);
       y8 <= y7 - (x7 >>> 7);
       z8 <= z7 + `rot7;
   end
   else  begin
       x8 <= x7 - (y7 >>> 7);
       y8 <= y7 + (x7 >>> 7);
       z8 <= z7 - `rot7;
   end
end

always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        x9 <= 1'b0;                         
        y9 <= 1'b0;
        z9 <= 1'b0;
    end
    else if( !y8[31] )  begin
       x9 <= x8 + (y8 >>> 8);
       y9 <= y8 - (x8 >>> 8);
       z9 <= z8 + `rot8;
   end
   else  begin
       x9 <= x8 - (y8 >>> 8);
       y9 <= y8 + (x8 >>> 8);
       z9 <= z8 - `rot8;
   end
end

always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        x10 <= 1'b0;                        
        y10 <= 1'b0;
        z10 <= 1'b0;
    end
    else if( !y9[31] )  begin
       x10 <= x9 + (y9 >>> 9);
       y10 <= y9 - (x9 >>> 9);
       z10 <= z9 + `rot9;
   end
   else  begin
       x10 <= x9 - (y9 >>> 9);
       y10 <= y9 + (x9 >>> 9);
       z10 <= z9 - `rot9;
   end
end

always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        x11 <= 1'b0;                        
        y11 <= 1'b0;
        z11 <= 1'b0;
    end
    else if( !y10[31] )  begin
       x11 <= x10 + (y10 >>> 10);
       y11 <= y10 - (x10 >>> 10);
       z11 <= z10 + `rot10;
   end
   else  begin
       x11 <= x10 - (y10 >>> 10);
       y11 <= y10 + (x10 >>> 10);
       z11 <= z10 - `rot10;
   end
end

always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        x12 <= 1'b0;                        
        y12 <= 1'b0;
        z12 <= 1'b0;
    end
    else if( !y11[31] )  begin
       x12 <= x11 + (y11 >>> 11);
       y12 <= y11 - (x11 >>> 11);
       z12 <= z11 + `rot11;
   end
   else  begin
       x12 <= x11 - (y11 >>> 11);
       y12 <= y11 + (x11 >>> 11);
       z12 <= z11 - `rot11;
   end
end

always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        x13 <= 1'b0;                        
        y13 <= 1'b0;
        z13 <= 1'b0;
    end
    else if( !y12[31] )  begin
       x13 <= x12 + (y12 >>> 12);
       y13 <= y12 - (x12 >>> 12);
       z13 <= z12 + `rot12;
   end
   else  begin
       x13 <= x12 - (y12 >>> 12);
       y13 <= y12 + (x12 >>> 12);
       z13 <= z12 - `rot12;
   end
end

always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        x14 <= 1'b0;                        
        y14 <= 1'b0;
        z14 <= 1'b0;
    end
    else if( !y13[31] )  begin
       x14 <= x13 + (y13 >>> 13);
       y14 <= y13 - (x13 >>> 13);
       z14 <= z13 + `rot13;
   end
   else  begin
       x14 <= x13 - (y13 >>> 13);
       y14 <= y13 + (x13 >>> 13);
       z14 <= z13 - `rot13;
   end
end

always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        x15 <= 1'b0;                        
        y15 <= 1'b0;
        z15 <= 1'b0;
    end
    else if( !y14[31] )  begin
       x15 <= x14 + (y14 >>> 14);
       y15 <= y14 - (x14 >>> 14);
       z15 <= z14 + `rot14;
   end
   else  begin
       x15 <= x14 - (y14 >>> 14);
       y15 <= y14 + (x14 >>> 14);
       z15 <= z14 - `rot14;
   end
end

//第16级迭代
always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        x16 <= 1'b0;                        
        y16 <= 1'b0;
        z16 <= 1'b0;
    end
    else if( !y15[31] )  begin
       x16 <= x15 + (y15 >>> 15);
       y16 <= y15 - (x15 >>> 15);
       z16 <= z15 + `rot15;
   end
   else  begin
       x16 <= x15 - (y15 >>> 15);
       y16 <= y15 + (x15 >>> 15);
       z16 <= z15 - `rot15;
   end
end

 

（4）将所得值赋给输出信号sqrt、actan，此处应该注意x16=K*sqrt（x^2+y^2），输出复数模值时需要除以K或乘以1/K，直接使用除法或乘法器都是非常消耗硬件资源的，因此采用移位的方式除以K（K为常数，具体得出的方式见上面的参考文献），因为输入的数据为了避免浮点运算，均扩大了2^16倍，所以输出的数据也扩大了2^16倍，右移16位的得到输出（但是应注意，这样得到的输出是整数，而无法得到小数的输出，只是为了便于特定数据仿真结果的验证，实际输出时不能采用这种移位方式）

 

always @ (posedge clk or negedge rst_n)
begin
    if( !rst_n )  begin
        sqrt <= 1'b0;
		  actan <= 1'b0;
    end
    else  begin  
      ppp <= (x16 >>> 1) + (x16 >>> 3) - (x16 >>> 6) - (x16 >>> 9);  //相当于x16/0.607523
       sqrt <= ppp >>> 16;
		 aaa <= z16;
		 actan <= aaa >>> 16;
	//	 sqrt <= x16;
    end
end

 

 

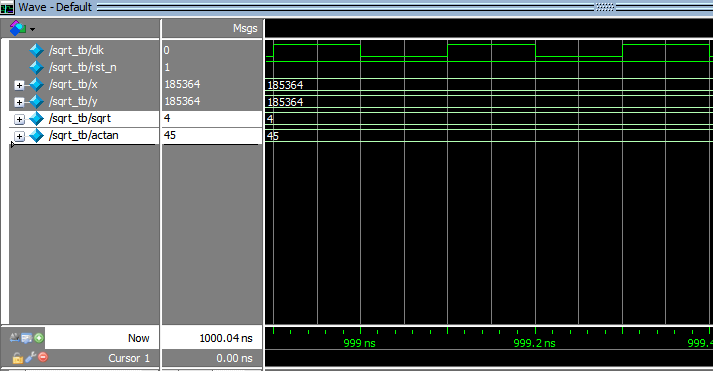
输入x=y=(2√2)*2^16=185364，预计输出sqrt=4，actan=45  （sqrt(8+8) = 4，tan45 = 1）