$ POJ~1966~Cable~TV~Network $
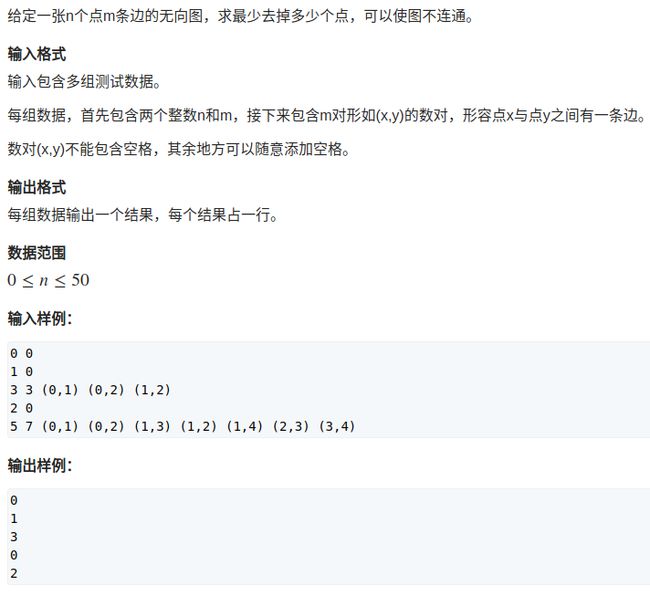
$ solution: $
第一眼可能让人很难下手,但本就是冲着网络流来的,所以我们直接一点。这道题我们要让这个联通图断开,那么势必会有两个点变得不连通,这道题的数据范围很小,所以我们试着暴力枚举两个点。这样就变成了最小割。不过,嗯?割的东西怎么是点?
为了靠近我们已经学得知识,我们想办法看,能不能割点变成割边。反正网络流最喜欢千变万化、左右建模了。。。于是我们引进书上的一个东西:
- 一个节点可以拆成两个节点,将原节点用中间那条边表示
- 一条边可以拆成两条边,将原边用中间那个点表示
- 中间的边权为1代表这个点是否被割,旁边的边权为inf是为了排除其影响(因为它不可能被割掉)
我们用第一条和第三条性质可以解决这个问题。首先对于每个节点建立两个 $ i $ 和 $ i+n $ 节点。然后这两个节点之间用一条权值为1的有向边(从 $ i $ 到 $ i+n $ ) ,如果这条边在最小割中被割掉(等价于原本的点被割掉)。然后 $ i $ 节点连入边(权值正无穷), $ i+n $ 节点连出边(权值正无穷),连正无穷是为了让割掉的边只能是中间的边。然后我们跑一遍最大流,它对应的最小割里每条代表原来一个点,因为权值为1,所以流量就是答案。
注意:我们的源汇点也要被分为两个点,而网络流中的实际源点是 $ S+n $ ,它连出边。因为源汇点的性质,这两个点不可能被割掉,所以它们中间不连边。
$ code: $
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
