小世界网络中的SIRS传染病模型实现

小世界网络

小世界网络模型是Watts和Strogatz于1998提出的一种描述现实社交关系网络的模型，该模型体现了现实社交网络中同质性和弱联系，使得“六度分隔”现象有了理论依据，解释了为什么两个陌生人之间通过少量的中间人就可以建立起联系。同质性意味着现实生活中存在大量的强三元闭包这类的结构，也就是彼此熟悉的人之间亲近的关系；弱联系意味着在除去每天接触的关系亲密的人之外，每个人的社交网络中还包括着一些距离较远的朋友，这些朋友在实现六度分隔理论中起到了至关重要的作用，这也就是小世界网络成功的地方。

SIRS传染病模型

该模型将动物状态分为三个类别：易感状态（S）、传染状态（I）、移出状态（R），易感状态的动物在与感染状态的动物接触过程中会以一定概率被传染状态的动物传染而患病；传染状态的动物可以一定的概率将疾病传染给接触到的动物；传染状态的动物在经历一段时间之后得到痊愈并且不再会收到感染，也不会对其他动物造成威胁，即相当于从整体中被移出的状态；在一段时间过后，移出状态的个体会再复原成为易感状态。在初始时一定比例的动物处于感染状态，剩余动物处于易受感染状态。

MATLAB实现

具体实现步骤如下：
首先建立小世界网络，假定网络中共有5000个节点，每个人和与其相邻的2k=6个的人之间形成联系，之后以0.1的概率消除某些边并随机建立数量相等的远程边，在这个过程中保证不形成重复的边和自环。

%create the small world network
%initial parameter
n = 5000;
k = 3;
p = 0.1;
mat = zeros(n);
%initial the circle
for i=1:n
   for j=i+1:i+k
      jj = j;
      if jj>n
         jj = mod(jj,n); 
      end
      mat(i,jj)=1;mat(jj,i)=1;
   end
end
%create weak connection
for i=1:n
   for j=i+1:i+k
      jj = j;
      if jj>n
          jj = mod(jj,n);
      end
      p1 = rand(1);
      if p1
i,jj)=0;mat(jj,i)=0;
         mat(i,i) = inf;
         a = find(mat(i,:)==0);
         r = randi(length(a));
         jjj = a(r);
         mat(i,jjj)=1;mat(jjj,i)=1;
         mat(i,i)=0;
      end
   end
end

这段代码实现了上面建立的小世界网络的可视化，然而结果并不是很好看orz

xa = zeros(n*n,1);
ya = zeros(n*n,1);
k=1;
for i=1:n
   for j=1:n
      if mat(i,j)==1
         xa(k)=i;
         ya(k)=j;
         k=k+1;
      end
   end
end
scatter(xa,ya)

接下来在该小世界网络中运行传染病模型，由于构建的网络中节点数量较多，所以运行速度会非常慢。具体实现过程中，先随机选择了10%的节点使其感染疾病，之后在感染的过程中，对每个易感状态的个体计算其相邻节点中感染疾病的节点与全部节点的比例来作为这个个体被感染的概率。最后将每个时刻全部节点中感染疾病的比例进行了绘图。

state = zeros(n,1);
sus = 1;
infe = 2;
recov = 3;
t = zeros(n,1);
ti = 4;
tr = 5;
to = ti+tr;
inip = 0.1;
%initialize the infection
for i=1:n
   r = rand(1);
   if ri) = infe;
       t(i) = 1;
   else
      state(i) = sus;
      t(i) = 0;
   end
end
%begin infection
period = 1000;
rate = zeros(period,1);
for k=1:period
   cnt = 0;
   for i=1:n
       if t(i)==0
           neigh = find(mat(i,:)==1);
           neighn = length(neigh);
           neighi = length(find(state(neigh)==infe));
           prob = neighi/neighn;
           r = rand(1);
           if ri) = 1;
           else
               t(i) = 0;
           end
       elseif t(i)>=1 && t(i)i) = t(i)+1;
       elseif t(i)==to
           t(i) = 0;
       end

       if t(i) == 0
           state(i) = sus;
       elseif t(i)>=1 && t(i)<=ti
           state(i) = infe;
           cnt=cnt+1;
       else
           state(i) = recov;
       end

   end
   rate(k) = cnt/n;

end
for i=1:period
   plot(1:1:k, rate(1:k));
   hold on 
end

模型运行结果

仿照了课本上的对该模型的探究，我对远程边形成概率p=0.01,0.2,0.5这个参数进行了探究，分别运行动态仿真结果如下：

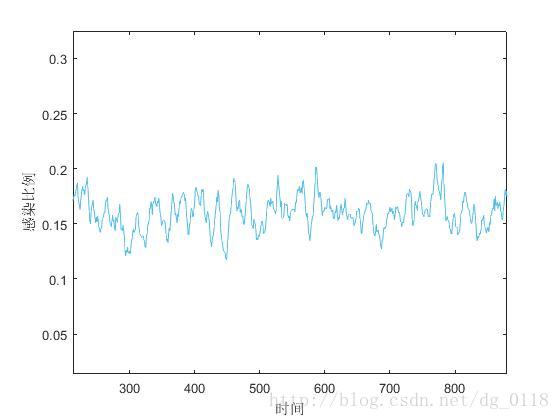
在p=0.01时的运行结果：

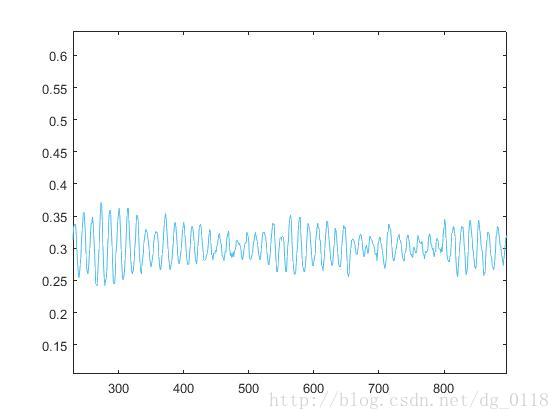
在p=0.2时的运行结果：

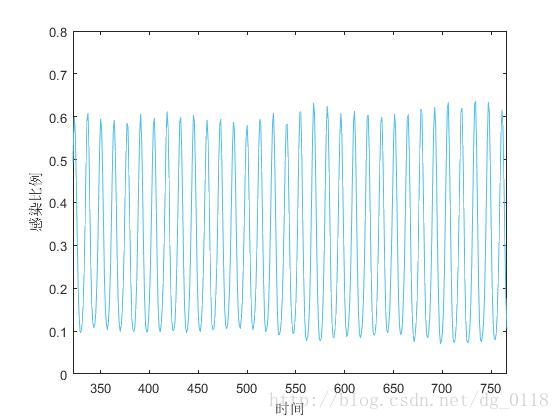
在p=0.5时的运行结果：

可以看到与课本上的结果也是相符合的，在远程边数量较少的时候，传染病的传播呈现在小区域范围内局部震荡的现象；而当远程边数量较多时，疾病在传播呈现周期性震荡的特征。