从零开始的机器学习生活---决策树
从零开始的机器学习生活—决策树的实现
代码下载地址:http://download.csdn.net/download/dh_nwu/10122106
决策树(decision tree)是一种常见的机器学习方法,往往不需要很深奥的背景知识就能掌握,所以选择决策树作为入门机器学习的第一款算法的你,已经成功迈出了成为机器学习大神的第一步。
学习决策树树之前,需要掌握数据结构树的知识,还需要有一定的python基础。对于没有接触过Python,且英文好的童鞋,这里推荐一本《Learn Python3 The Hard Way》,英文不好的童鞋也没关系,推荐你们看《Head First Python》(又名《深入浅出python》)
1.决策树介绍
什么是决策树呢?简单的来说,可以理解为一个树形结构的流程图,从根节点开始,每一个内部节点都对应一个属性测试,根节点则对应一个决策结果。如图所示,输入当前的环境信息,即可知道今天是否应该出门。
2.数据处理
什么样的数据可以用来训练决策树?决策树属于监督学习(supervised learning)的一种,需要从有标号的训练元组中学习并产生。如下图所示,已知{色泽、根蒂、敲声、纹理、脐部、触感}的属性信息,也知道对应的结果{好瓜/坏瓜},即可采用不同的属性选择度量产生分裂节点。
为了方便计算,将数据构建成了一个二维列表data,在“色泽“属性中,将青绿设为1,乌黑设为2,浅白设成3……并用’y’,’n’来表示好瓜、坏瓜。构建一个属性列表label,用于存放对应的属性名。
data = [[1, 1, 1, 1, 1, 1, 'y'],#编号为1的元组
[2, 1, 2, 1, 1, 1, 'y'],#编号为2的元组
[2, 1, 1, 1, 1, 1, 'y'],
[1, 1, 2, 1, 1, 1, 'y'],
[3, 1, 1, 1, 1, 1, 'y'],
[1, 2, 1, 1, 2, 2, 'y'],
[2, 2, 1, 2, 2, 2, 'y'],
[2, 2, 1, 1, 2, 1, 'y'],
[2, 2, 2, 2, 2, 1, 'n'],
[1, 3, 3, 1, 3, 2, 'n'],
[3, 3, 3, 3, 3, 1, 'n'],
[3, 1, 1, 3, 3, 2, 'n'],
[1, 2, 1, 2, 1, 1, 'n'],
[3, 2, 2, 2, 1, 1, 'n'],
[2, 2, 1, 1, 2, 2, 'n'],
[3, 1, 1, 3, 3, 1, 'n'],
[1, 1, 2, 2, 2, 1, 'n'], ]
label = ['color', 'root', 'sound', 'pattern', 'stomach', 'feel', 'good']
3.属性划分
3.1. 信息增益(ID3算法)
下图是信息熵的计算公式,Ent(D)是属性D的信息熵,Ent(D)越小,D的纯度越高。
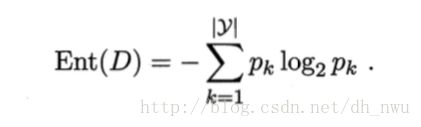
python表示如下图所示:
def Ent(data): # 计算总体的信息熵
numP = numN = 0
temp = 0
last = [x[-1] for x in data]#将'y','n'提取出来,存放到列表last中
for x in last:#分别用numP和numN表示'y'和'n'的数量
if x == 'y':
numP += 1
else:
numN += 1
if numP != 0:#分开计算是因为在log(n,2)中,如果n=0,log(n,2)取值不存在。
temp -= ((numP / len(data)) * math.log(numP / len(data), 2))
if numN != 0:
temp -= ((numN / len(data)) * math.log(numN / len(data), 2))
return temp
下图中Gain(D,a)的含义是属性a对样本集划分的信息增益,信息增益越大,则用a划分的效果最好。
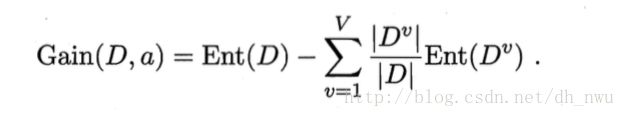
以下是将公式用代码表示的形式,为了简化运算,将属性的子属性的最大数量设置为三个,即色泽属性中有青绿、乌黑、浅白三种子属性。
def Gain(data, label, attribute): # 计算信息增益;attribute是属性名;属性的子属性最大为三个
attribute1 = attribute2 = attribute3 = 0
num = label.index(attribute)
diffAttribute = [x[num] for x in data]
for x in diffAttribute:
if x == 1:
attribute1 += 1
elif x == 2:
attribute2 += 1
else:
attribute3 += 1
attriData1 = [x for x in data if x[num] == 1]
attriData2 = [x for x in data if x[num] == 2]
attriData3 = [x for x in data if x[num] == 3]
return Ent(data) - (attribute1 / len(data)) * Ent(attriData1) - (attribute2 / len(data)) * Ent(attriData2) - (attribute3 / len(data)) * Ent(attriData3)例如,当我们使用“色泽“进行划分,则运算过程如下图所示
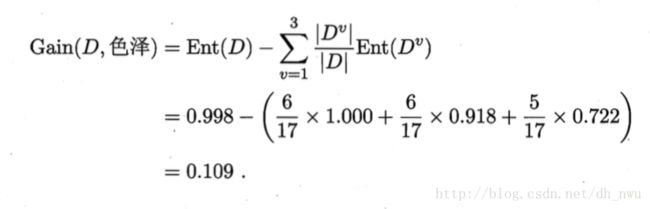
计算其他属性的信息增益的结果为:
Gain(D,根蒂) = 0.143;
Gain(D,敲声) = 0.141;
Gain(D,纹理) = 0.381;
Gain(D,脐部) = 0.289;
Gain(D,触感) = 0.006;
通过“纹理“划分的信息增益最大,所以应该使用“纹理“作为划分属性。
计算信息增益的函数如下:通过调用Gain(data,label,attribute)函数,返回最大的结果,返回的格式为[0.3805918973682686, ‘pattern’]
def ID3(data, label): # 计算出最大的信息增益
temp = [0, 0]
for x in label[:-1]:
if Gain(data, label, x) > temp[0]:
temp = [Gain(data, label, x), x]
return temp # 返回[最大的信息增益,属性]3.2 信息熵(C4.5算法)
信息增益划分属性存在一种问题是,信息增益准则对可取值数目多的属性有所偏好。比如说如果我们通过西瓜的编号进行划分时,会产生非常多的划分属性,每一个编号都可能被划分为一个叶节点。
为了消除取值数目多产生的属性偏好,著名的C4.5算法采用增益率来划分属性,增益率的计算公式如下所示:
def splitInfo(data,label,attribute):
attribute1 = attribute2 = attribute3 = 0
Split1 = Split2 = Split3 = 0
num = label.index(attribute)
diffAttribute = [x[num] for x in data]
for x in diffAttribute:
if x == 1:
attribute1 += 1
elif x == 2:
attribute2 += 1
else:
attribute3 += 1
attriData1 = [x for x in data if x[num] == 1]
attriData2 = [x for x in data if x[num] == 2]
attriData3 = [x for x in data if x[num] == 3]
if len(attriData1) != 0:
Split1 = - (len(attriData1) / len(data)) * math.log((len(attriData1) / len(data)),2)
if len(attriData2) != 0:
Split2 = - (len(attriData2) / len(data)) * math.log((len(attriData2) / len(data)),2)
if len(attriData3) != 0:
Split3 = - (len(attriData3) / len(data)) * math.log((len(attriData3) / len(data)),2)
return Split1 + Split2 + Split3
def GainRatio(data,label,attribute):
return Gain(data,label,attribute)/splitInfo(data,label,attribute)
def C4point5(data,label):
temp = [0, 0]
for x in label[:-1]:
if GainRatio(data, label, x) > temp[0]:
temp = [GainRatio(data, label, x), x]
return temp
print(C4point5(data,label))11月19号更新:新加了C4.5的代码,但没有放到下载文件里,就放倒博客里大家看一下实现过程吧。
3.3 基尼指数(CART算法)
CART算法使用基尼指数来划分属性,Gini(D)越小,数据集的纯度越高:

属性a的基尼指数的定义如下图所示:
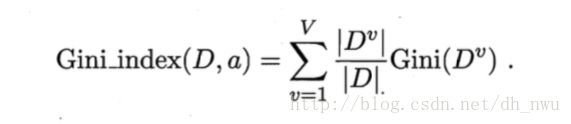
基尼指数考虑了每个属性的二元划分。比如说,如果使用色泽作为划分属性,色泽的值{青绿、乌黑、浅白}的所有真子集{青绿、乌黑},{青绿、浅白},{乌黑、浅白},{青绿},{乌黑},{浅白},都可以作为二元划分。
,对于离散值属性,应该选择最小基尼指数的子集作为分裂子集。
4.决策树训练
决策树的产生是一个递归过程,有三个地方需要注意递归返回
- 当前节点全部属于同一类别,无需划分;
- 当前属性集为空,或者所有属性集相同,无法划分;
- 当前节点包含的样本集合为空,不能划分。
def decisionTree(data, label):
temp = [x[-1] for x in data]
if temp.count('y') == 0 and temp.count('n') != 0:#(1)data中的元组在同一类中,标记为叶节点
return '坏瓜'
if temp.count('n') == 0 and temp.count('y') != 0:
return '好瓜'
if len(label) < 2:#(2)属性集为空,或者当前样本在当前属性下取值相同,标记为叶节点
return
node = ID3(data, label)
num = label.index(node[1])
myTree = {node[1]:{}}
for x in range(1, 4):
attriDataTemp = [y for y in data if y[num] == x]
attriData = copy.deepcopy(attriDataTemp[:])
if len(attriData) < 1:
return myTree#(3)当前节点的样本集为空,已经全部划分,标记为分支节点
else:
for y in range(0, len(attriData)): # 删除属性信息
del (attriData[y][label.index(node[1])])
temp1 = copy.deepcopy(label[:])
temp1.remove(node[1])
myTree[node[1]][x] = decisionTree(attriData, temp1)
return myTree最终产生的决策树如下图所示:
![]()
字符串的树结构的描述为:{‘pattern’: {1: {‘root’: {1: ‘好瓜’, 2: {‘color’: {1: ‘好瓜’, 2: {‘feel’: {1: ‘好瓜’, 2: ‘坏瓜’}}}}, 3: ‘坏瓜’}}, 2: {‘feel’: {1: ‘坏瓜’, 2: ‘好瓜’}}, 3: ‘坏瓜’}}
5. 总结
决策树的原理是比较容易理解的,在学习每一种算法的时候,最好能够用代码把算法实现一下,这样理解的效果会深刻。
实际上,决策树还涉及了先剪枝、后剪枝、连续值、缺省值的处理等等,而且划分属性也不只以上三种,这些都是在实际问题中需要处理的问题。
参考书籍:
《机器学习》周志华 清华大学出版社
《数据挖掘 概念与技术》 Jiawei Han,Micheline Kamber,Jian Pei 第三版



