压缩感知的实现(含matlab代码)
压缩感知的图像重建(matlab)
https://blog.csdn.net/Di_Wong/article/details/88994551
目录
原理简介
算法实现
测试结果
---------------------------------------------------------------------------------------------------------------------------------------------
原理参考
(1)刘海英. 基于压缩感知理论的高光谱图像重建和超分辨成像技术研究[D]. 西安电子科技大学, 2014.
(2)压缩感知的常见稀疏基名称及离散傅里叶变换基
(3)压缩感知的常见测量矩阵
算法参考
(1)压缩感知重构算法之正交匹配追踪(OMP)
----------------------------------------------------------------------------------------------------------------------------------------------
原理简介
压缩感知(Compressive Sensing,CS)。相对于传统的奈奎斯特采样定理——要求采样频率必须是信号最高频率的两倍或两倍以上(这就要求信号是带限信号,通常在采样前使用低通滤波器使信号带限),压缩感知则利用数据的冗余特性,只采集少量的样本还原原始数据。
一句话总结我理解的压缩感知实现方法:以被重建信号在某个变换域上稀疏作为先验信息,用测量矩阵观测被测信号,由观测值结合重建算法重建出完整的被测信号。
在具体应用时,我们必须解决 CS 理论的三大关键问题:
- 目标信号的稀疏表示。寻找使得目标信号 f 变换到其上尽可能稀疏的变换域Ψ ,即信号稀疏表示问题;
- 测量矩阵的构建。测量矩阵是 CS 理论采样的实现部分。通过测量矩阵控制的采样使得目标信号 f在采样过程中即被压缩,同时保证目标信号所含有效信息不丢失,能够由压缩采样值还原出目标信号;
- 重建算法的设计。重建算法是从采样值求解最优化问题寻找到目标信号最优解。重建算法的准确性、高效性和稳定性是其设计的关键。
对于目标信号的稀疏表示问题,常见的稀疏基有离散余弦变换基(DCT)和快速傅立叶变换基(FFT)等。
对于测量矩阵,常见的有高斯随机矩阵、部分哈达玛矩阵等。
对于重建算法,常见的有L1范数、正交匹配追踪算法(OMP)等。
对于原理部分,相关文献、博客等资源相当多,本文不在这里赘述,详情可以参考本文开头引用内容。
算法实现
本文分别以稀疏基有离散余弦变换基(DCT)和快速傅立叶变换基(FFT)做为稀疏基,高斯随机矩阵、部分哈达玛矩阵为测量矩阵,L1范数、正交匹配追踪算法(OMP)为重建算法进行压缩感知算法实现。
本文以f = cos(2*pi/256*t) + sin(2*pi/128*t)做为原信号,取原信号f的20%做为输入进行压缩感知重建。
注意:本文main.m中L1范数求解方法使用了CVX工具箱,CVX工具箱安装方法参考(CVX工具包(for matlab))
main.m
% 该程序用于验证压缩感知理论(包含了L1最小范数求解和OMP求解)
%
%
%
clear all; close all;
%% 产生信号
choice_transform = 1; % 选择正交基,1为选择DCT变换,0为选择FFT变换
choice_Phi = 0; %选择测量矩阵,1为部分哈达玛矩阵,0为高斯随机矩阵
%-----------------------利用三角函数生成频域或DCT域离散信号--------------------------
n = 512;
t = [0: n-1];
f = cos(2*pi/256*t) + sin(2*pi/128*t); % 产生频域稀疏的信号
%-------------------------------信号降采样率-----------------------
n = length(f);
a = 0.2; % 取原信号的 a%
m = double(int32(a*n));
%--------------------------------------画信号图--------------------------------------
switch choice_transform
case 1
ft = dct(f);
disp('ft = dct(f)')
case 0
ft = fft(f);
disp('ft = fft(f)')
end
disp(['信号稀疏度:',num2str(length(find((abs(ft))>0.1)))])
figure('name', 'A Tone Time and Frequency Plot');
subplot(2, 1, 1);
plot(f);
xlabel('Time (s)');
% ylabel('f(t)');
subplot(2, 1, 2);
switch choice_transform
case 1
plot(ft)
disp('plot(ft)')
case 0
plot(abs(ft));
disp('plot(abs(ft))')
end
xlabel('Frequency (Hz)');
% ylabel('DCT(f(t))');
%% 产生感知矩阵和稀疏表示矩阵
%--------------------------利用感知矩阵生成测量值---------------------
switch choice_Phi
case 1
Phi = PartHadamardMtx(m,n); % 感知矩阵(测量矩阵) 部分哈达玛矩阵
case 0
Phi = sqrt(1/m) * randn(m,n); % 感知矩阵(测量矩阵) 高斯随机矩阵
end
% Phi = randn(m,n); %randn 生成标准正态分布的伪随机数(均值为0,方差为1)
% Phi = rand(m,n); % rand 生成均匀分布的伪随机数。分布在(0~1)之间
f2 = (Phi * f')'; % 通过感知矩阵获得测量值
% f2 = f(1:2:n);
switch choice_transform
case 1
Psi = dct(eye(n,n)); %离散余弦变换正交基 代码亦可写为Psi = dctmtx(n);
disp('Psi = dct(eye(n,n));')
case 0
Psi = inv(fft(eye(n,n))); % 傅里叶正变换,频域稀疏正交基(稀疏表示矩阵)
disp('Psi = inv(fft(eye(n,n)));')
end
A = Phi * Psi; % 恢复矩阵 A = Phi * Psi
%% 重建信号
%---------------------使用CVX工具求解L1范数最小值-----------------
cvx_begin;
variable x(n) complex;
% variable x(n) ;
minimize( norm(x,1) );
subject to
A*x == f2' ;
cvx_end;
figure;subplot(2,1,2)
switch choice_transform
case 1
plot(real(x));
disp('plot(real(x))')
case 0
plot(abs(x));
disp(' plot(abs(x))')
end
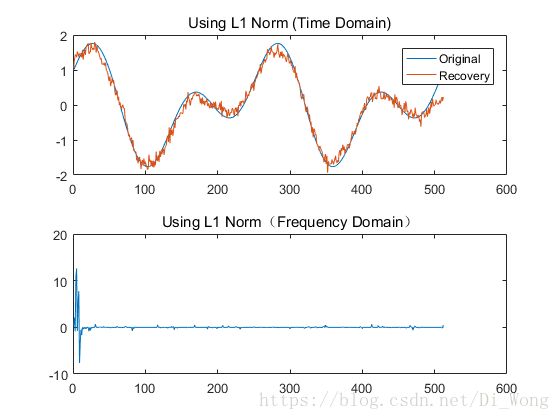
title('Using L1 Norm(Frequency Domain)');
% ylabel('DCT(f(t))'); xlabel('Frequency (Hz)');
switch choice_transform
case 1
sig = dct(real(x));
disp('sig = dct(real(x))')
case 0
sig = real(ifft(full(x)));
disp(' sig = real(ifft(full(x)))')
end
subplot(2,1,1);
plot(f)
hold on;plot(sig);hold off
title('Using L1 Norm (Time Domain)');
% ylabel('f(t)'); xlabel('Time (s)');
legend('Original','Recovery')
%-----------------------------使用OMP算法重建--------------------------
for K = 1:100
theta = CS_OMP(f2,A,K);
% figure;plot(dct(theta));title(['K=',num2str(K)])
switch choice_transform
case 1
re(K) = norm(f'-(dct(theta)));
case 0
re(K) = norm(f'-real(ifft(full(theta))));
end
end
theta = CS_OMP(f2,A,find(re==min(min(re))));
disp(['最佳稀疏度K=',num2str(find(re==min(min(re))))]);
% theta = CS_OMP(f2,A,10);
figure;subplot(2,1,2);
switch choice_transform
case 1
plot(theta);
disp('plot(theta)')
case 0
plot(abs(theta));
disp('plot(abs(theta))')
end
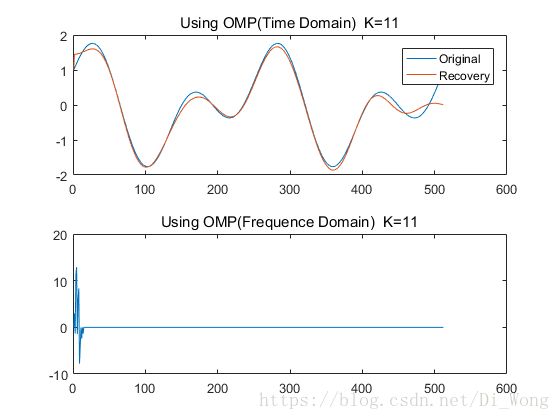
title(['Using OMP(Frequence Domain) K=',num2str(find(re==min(min(re))))])
switch choice_transform
case 1
sig2 = dct(theta);
disp('sig2 = dct(theta)')
case 0
sig2 = real(ifft(full(theta)));
disp('sig2 = real(ifft(full(theta)))')
end
subplot(2,1,1);plot(f);hold on;
plot(sig2)
hold off;
title(['Using OMP(Time Domain) K=',num2str(find(re==min(min(re))))]);
legend('Original','Recovery')
%%
其中调用函数
部分哈达玛矩阵:PartHadamardMtx.m
function [ Phi ] = PartHadamardMtx( M,N )
%PartHadamardMtx Summary of this function goes here
% Generate part Hadamard matrix
% M -- RowNumber
% N -- ColumnNumber
% Phi -- The part Hadamard matrix
% 来源http://blog.csdn.net/jbb0523/article/details/44700735
%% parameter initialization
%Because the MATLAB function hadamard handles only the cases where n, n/12,
%or n/20 is a power of 2
L_t = max(M,N);%Maybe L_t does not meet requirement of function hadamard
L_t1 = (12 - mod(L_t,12)) + L_t;
L_t2 = (20 - mod(L_t,20)) + L_t;
L_t3 = 2^ceil(log2(L_t));
L = min([L_t1,L_t2,L_t3]);%Get the minimum L
%% Generate part Hadamard matrix
Phi = [];
Phi_t = hadamard(L);
RowIndex = randperm(L);
Phi_t_r = Phi_t(RowIndex(1:M),:);
ColIndex = randperm(L);
Phi = Phi_t_r(:,ColIndex(1:N));
end 正交匹配追踪算法:OMP.m
function [ theta ] = CS_OMP( y,A,t )
% 实现压缩感知OMP算法
%CS_OMP Summary of this function goes here
%Version: 1.0 written by jbb0523 @2015-04-18
% Detailed explanation goes here
% y = Phi * x
% x = Psi * theta
% y = Phi*Psi * theta
% t 稀疏度
% 令 A = Phi*Psi, 则y=A*theta
% 现在已知y和A,求theta
% 来源:http://blog.csdn.net/jbb0523/article/details/45130793
[y_rows,y_columns] = size(y);
if y_rows