R语言执行T检验

说明

a.单样本t检验可以帮助我们测试两个均值是否存在显著性差异
b.双样本t检验可以用来测试两组独立的数据集其均值是否不同

#导入数据
library(stats)
data("mtcars")
#操作
1）完成属性可视化处理，在盒图中分别展示mpg和am两个属性的差别：
boxplot(mtcars$mpg,mtcars$mpg[mtcars$am==0],ylab = "mpg",names = c("overall","automobile"))

boxplot(mtcars$mpg,mtcars$mpg[mtcars$am==0],ylab = "mpg",names = c("overall","automobile"))

abline(h = mean(mtcars$mpg),lwd = 2,col = "red")

abline(h = mean(mtcars$mpg[mtcars$am==0]),lwd = 2,col = "blue")

#执行统计分析来验证汽车类型的样本mpg均值是否低于总体样本的mpg值：
mpg.meanall = mean(mtcars$mpg)
mpg_am = mtcars$mpg[mtcars$am == 0]
t.test(mpg_am,mu = mpg.meanall)

    One Sample t-test

data:  mpg_am
t = -3.3462, df = 18, p-value = 0.003595
alternative hypothesis: true mean is not equal to 20.09062
95 percent confidence interval:
 15.29946 18.99528
sample estimates:
mean of x 
 17.14737  

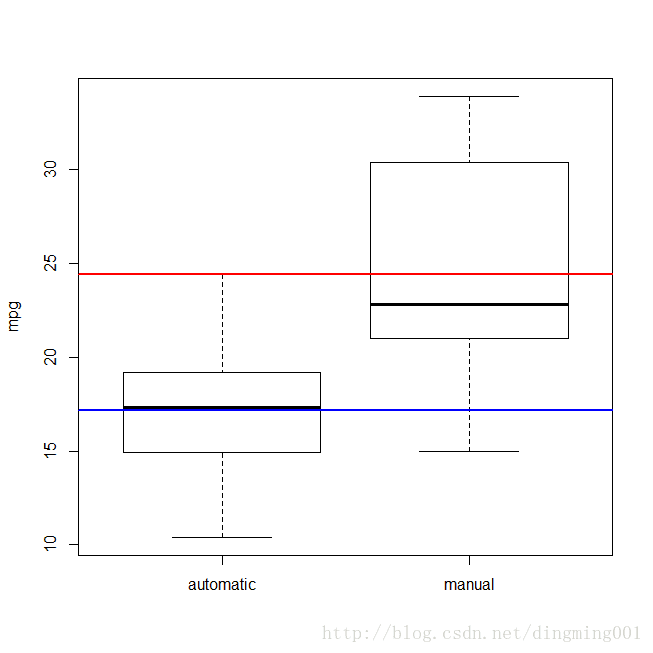
#采用盒图分析绘制结果，手动与自动的对比，红蓝线分别表示各自平均数
boxplot(mtcars$mpg~mtcars$am,ylab = "mpg",names = c("automatic","manual"))
#这条程序与之等价
boxplot(mtcars$mpg[mtcars$am==0],mtcars$mpg[mtcars$am==1],ylab = "mpg",names = c("automatic","manual"))
abline(h = mean(mtcars$mpg[mtcars$am==0]),lwd = 2,col = "blue")
abline(h = mean(mtcars$mpg[mtcars$am==1]),lwd = 2,col = "red")

#接下来分析自动档车的mpg值是否低于手动档的mpg
 t.test(mtcars$mpg~mtcars$am)

    Welch Two Sample t-test

data:  mtcars$mpg by mtcars$am
t = -3.7671, df = 18.332, p-value = 0.001374
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -11.280194  -3.209684
sample estimates:
mean in group 0 mean in group 1 
       17.14737        24.39231 
 #注意两种间隔符的区别，可以表示相当意思 
 t.test(mtcars$mpg[mtcars$am==0],mtcars$mpg[mtcars$am==1])

    Welch Two Sample t-test

data:  mtcars$mpg[mtcars$am == 0] and mtcars$mpg[mtcars$am == 1]
t = -3.7671, df = 18.332, p-value = 0.001374
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -11.280194  -3.209684
sample estimates:
mean of x mean of y 
 17.14737  24.39231 

分析

a.单样本检验中，由红蓝线的高度人们会有自动汽车的mpg的均值显著小于总体的mpg均值猜测。这为HO:u>=u0（原假设）,
H1:u < u0(这是人们的假设，备择假设)，u0代表总体mpg均值.我们使用了单样本t检验，得到的p-value = 0.003595，小于0.05,因此我们拒绝H0,接收H1，假设成立。

b.双样本检验中，可以判断两个均值是否有显著性差异。H0：u1=u2,H1：u1!=u2，p-value <0.05,拒绝H0,接收H1。假设成立。