网络流之最大流和最小割

最大流问题

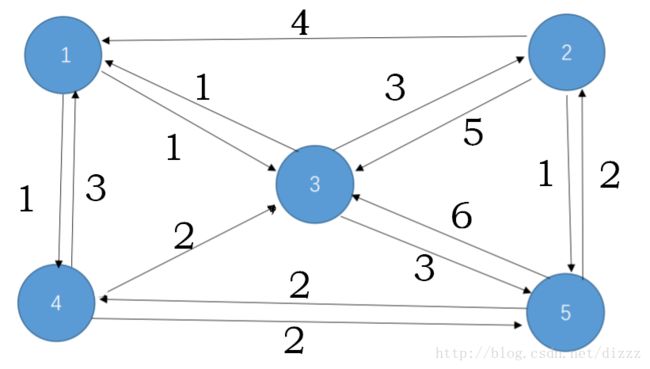
最大流：给定有向图中每条边的最大流量（容量），求从源点到汇点的最大流量。

容量网络: 括号左边代表容量，右边代表流量。

残留网络：流网络中剩余可增加的流量

增广路：满足容量条件的一条流量不为零的路径。

增广路定理：设容量网络G(V,E)的一个可行流为f，f为最大流的充要条件是在容量网络中不存在增广路。

Ford-Fulkson方法：搜索残留网络找增广路，直至找不到增广路（找到最大流）。

Edmonds-Karp算法:利用bfs搜索增广路的算法，复杂度O(VE2)

queue<int> que;
bool visited[MAXN];
int p[MAXN];
int Map[MAXN][MAXN];
bool bfs (int s, int t){
    memset (visited, false, sizeof(visited));
    memset (p, -1, sizeof(p));
    visited[s] = true;
    while(!que.empty()) que.pop();
    que.push(s);
    while (!que.empty()){
        int Top = que.front();
        if (Top == t)return true;
        que.pop();
        for (int i=1; i<=V; i++){
            if (Map[Top][i] && !visited[i]){
                visited[i] = true;
                que.push(i);
                p[i] = Top;
            }
        }
    }
    return false;
}
int edmond_skarp (int s,int t){
    int u,ret = 0,f;
    while (bfs(s,t)){
        f = INF;
        u = t;
        while (p[u] != -1){
            f = min (f, Map[p[u]][u]);
            u = p[u];
        }
        ret += f;
        u = t;
        while (p[u] != -1){
            Map[p[u]][u] -= f;
            Map[u][p[u]] += f;
            u = p[u];
        }
    }
    return ret;
}

层次网络：用bfs对残留网络进行分层后，删去比汇点层次更高的顶点和与汇点同层的顶点，并删去这些顶点关联的弧，再删去从某层顶点指向同层顶点和低层顶点的弧，所剩弧的容量和残留网络中的相同，得到的网络是层次网络。

Dinic算法：每次用bfs建立层次网络，再用dfs进行增广，当bfs后汇点不在层次网络中，算法结束。
算法复杂度O(V2E)

struct edge{int to,cap,rev;};
vectorG[MAXN];
int level[MAXN];
int iter[MAXN];
void bfs(int s){
    memset(level,-1,sizeof(level));
    queue<int> que;
    level[s] = 0;
    que.push(s);
    while(!que.empty()){
        int v = que.front(); que.pop();
        for(int i = 0; i < G[v].size(); i++){
            edge &e = G[v][i];
            if(e.cap > 0 && level[e.to] < 0){
                level[e.to] = level[v] +1;
                que.push(e.to);
            }
        }
    }
}
int dfs(int v,int t,int f){
    if(v == t) return f;
    for(int &i = iter[v]; i < G[v].size(); i++){
        edge &e = G[v][i];
        if(e.cap > 0 && level[v] < level[e.to]){
            int d = dfs(e.to,t,min(f,e.cap));
            if(d > 0){
                e.cap -= d;
                G[e.to][e.rev].cap += d;
            return d;
            }
        }
    }
    return 0;
}
int dinic(int s,int t){
    int flow = 0;
    while(1){
        bfs(s);
        if(level[t] < 0) return flow;
        memset(iter,0,sizeof(iter));
        int f;
        while(f = dfs(s,t,INF) > 0)
            flow += f; 
    }
}

在网络流问题中，最重要的是模型的建立和转换，也就是建图的过程。

网络流问题一般具有明显的变量的约束条件。

HDU3416
题意：问一个有向图中最短路的路径数量（在不同的路径中没有重复的边）。

思路：先用最短路算法求出最短路，找出最短路的路径。建一个新图，源点和汇点与原图的起点和终点相同。对于路径中的边，在新图中连一条容量为1的u到v的边，求出新图的最大流，即为路径的数量。
寻找最短路路径的问题：若dis[v]= dis[u] + cost[u][v] ,则是最短路中的边。

HDU3572
题意：
有n个任务(n<=500)，每个任务需要被处理Pi天才能完成，且只能在第Si到第Ei天(Si 思路：
把任务和每一天都看成点。建立一个源点向每个任务连一条容量为Pi的边，如果某一天能完成某个任务，则由这个任务向这一天连一条容量为1的边。每一天向汇点连一条容量为M的边。求最大流，如果最大流是满流（等于完成任务所需要的天数之和），则能完成所有任务。

HDU2883

题意:
n个人去吃烤肉（n<=200），每个人在si时刻来,ei时刻离开，点ni份烤肉，其中每份烤肉需要烤ti个单位时间。(1 <= si < ei <= 1000000)，烤肉店每个单位时间能同时烤m份烤肉，每块烤肉可以被分成任意大小烤，问烤肉店能否满足人们的需求。

思路：首先，要注意到，可以把ni块烤肉用ti的时间烤看作把ni* ti块烤肉用1个单位的时间烤。这道题需要用到离散化思想。和上题一样，把时间也看成点，不同的是这题要把时间段看成点。具体做法是把所有的si和ei从小到大排序,依次给每个时间间隔标号。源点向每个人连容量为ni* ti的边，如果某人的si和ei在时间内，这个人向区间连容量为INF的边，此外，每个区间向汇点连容量为m*(Ti-Ti-1)的边。

拆点：把点权转换为边权。

HDU2732

题意：有一个n*m的图，图上有一些柱子，每根柱子有一定的耐久度，在其中一些柱子上有蜥蜴（每根柱子最多有一只）， 蜥蜴的最大跳跃长度是d,当蜥蜴完成一次跳跃后，原先柱子的耐久度-1。问最多有多少蜥蜴能跳出这个图（跳出边缘）。

思路：需要选择每只蜥蜴的跳跃路径使得能让最多的蜥蜴跳出去。容易想到把一只蜥蜴的路径看作网络流中的一条流。建立一个源点s和汇点t,源点向所有有蜥蜴的点连一条容量为1的边。网络流的流量被点权限制，可以把每个点拆分为两个点u,v，边的权为点的权，把连向原点的边连给u点，v连接原点连出的点。如果能从当前点跳出，则在v和t 之间连一条容量为INF的边。

HDU4309

题意：有n个城市的人要进行避难，每个城市拥有的人数是ai，图上有三种边，一种是隧道，每个隧道可以庇护bi个人，第二种是普通的公路，可以通过任意数量的人，第三种是破桥（最多12座），只能通过1个人，但是破桥被修复之后也可以通过任意数量的人，修复的费用是ci，问能庇护的最大人数，同时求出修桥的最小费用。

思路：先不考虑修复桥的问题，容易建立一个网络流的模型。源点连接每个城市，容量为城市拥有的人数。公路是容量为INF的边，桥是容量为1的边。对于隧道，可以新建一个点，隧道两端的点到这个点的容量是INF，这个点到汇点的边的容量是隧道的容纳量。
由于桥的数量很小，所以可以状压枚举修桥的情况，求出每次的容纳人数和修桥费用。修理一座桥即在两个点之间再连一条容量为INF的边。

网络流与二分匹配：
二分图中的所有点可分为U集合和V集合，它们的交集为空集，二分图中的边一定连接了U集合和V集合中的两点。

将原图中所有的无向边变为有向边，容量为1。源点连接U,V连接汇点，容量都为1，最大流即为最大匹配。

HDU3468

题意：有个人在r*c的图上寻宝，图上有有一些无法到达的障碍和金子，他必须他每次必须从一个检查点（用大写字母和小写字母表示）经过最短路径到达下一个检查点（比如从A到B,B到C），途中最多捡起一块金子。问他最多能够捡起多少块金子。

思路：这是一个金子和检查点的最大匹配问题。途中经过的每一个检查点和路径中能够捡到的金子连接。然后用前面的方法求出最大匹配。

HDU3081

题意：婚礼上有n个boy和n个girl，每个girl可以和她喜欢的boy配对，同时，她也可以和她的女性朋友的喜欢的boy配对。在每一轮配对（所有girl找到各自配对的boy）之后，每个girl再选取之前没有配对过的boy进行配对，问这样的配对最多能够进行几轮。

思路：可以利用类似二分匹配的想法。二分进行的轮数r，每个女孩与她能配对的男孩子之间连一条容量为1的边（因为只能匹配一次）。源点向每个女孩连一条容量为r的边，男孩向汇点连一条容量为r的边，如果此时的最大流为r，则能够完成r次匹配。

割：去掉后使得图不连通的边的集合

割的容量：割中所有前向弧的容量的和

最小割：容量最小的割

最大流最小割定理：对容量网络G(V,E)，其最大流的容量等于最小割的容量

HDU5889 (2016ICPC青岛网络赛)

题意：给定一个无向图，图上每条边的长度是1，求删去权值和最小的边，使得图上的最短路都被切断。

思路：最大流最小割定理

HDU3046

题意：图上有n*m个方块（0

思路：源点向羊连容量为INF的边，狼向汇点连容量为INF的边，每个格子向与它相邻的格子连一条容量为1的边。