【算法基础实验】排序-最小索引优先队列IndexMinPQ

回顾最小优先队列MinPQ

理论知识

概述

在算法和数据结构中，优先队列是一种特殊的队列数据结构，每个元素都有一个优先级。当你从优先队列中删除元素时，通常会删除具有最高（或最低）优先级的元素。在最小优先队列中，优先级最低的元素最先被删除。

索引最小优先队列 是优先队列的一种变体，允许你通过索引（或键）快速地更新、插入、删除和访问最小元素。它的典型应用包括网络流、图算法（如Dijkstra最短路径算法）等。

基本操作

插入操作（insert）: 向优先队列中插入一个元素，并赋予它一个优先级。
删除最小元素（delMin）: 删除优先级最低的元素并返回它的索引。
更改优先级（changeKey/change）: 更改指定索引的元素的优先级。
查询是否包含指定索引的元素（contains）: 判断索引是否在队列中。
查询队列是否为空（isEmpty）: 判断队列是否为空。
查询队列中元素的数量（size）: 获取队列中的元素数量。
索引最小优先队列的实现
该数据结构通常用堆（二叉堆）来实现，堆的每个节点保存元素的索引，而优先级是通过另一个数组维护的。
插入和删除操作的时间复杂度为 O(log N)，其中 N 是队列中的元素数量。

实验数据

实验数据存在于main函数中

String[] strings = { "it", "was", "the", "best", "of", "times", "it", "was", "the", "worst" };

代码实现

import edu.princeton.cs.algs4.StdOut;

public class myIndexMinPQ<Key extends Comparable<Key>> {
    private int maxN;
    private int n;
    private int[] pq;
    private int[] qp;
    private Key[] keys;

    public myIndexMinPQ(int maxN) {
        this.maxN = maxN;
        n = 0;
        keys = (Key[]) new Comparable[maxN + 1];    // make this of length maxN??
        pq   = new int[maxN + 1];
        qp   = new int[maxN + 1];                   // make this of length maxN??
        for (int i = 0; i <= maxN; i++)
            qp[i] = -1;
    }

    public boolean isEmpty() {
        return n == 0;
    }

    public boolean contains(int i) {
        return qp[i] != -1;
    }

    public int size() {
        return n;
    }

    public void insert(int i, Key key) {
        n++;
        qp[i] = n;
        pq[n] = i;
        keys[i] = key;
        swim(n);
    }

    public int delMin() {
        int min = pq[1];
        exch(1, n--);
        sink(1);
        qp[min] = -1;        // delete
        keys[min] = null;    // to help with garbage collection
        pq[n+1] = -1;        // not needed
        return min;
    }

    public void changeKey(int i, Key key) {
        keys[i] = key;
        swim(qp[i]);
        sink(qp[i]);
    }

    public void change(int i, Key key) {
        changeKey(i, key);
    }

    private boolean greater(int i, int j) {
        return keys[pq[i]].compareTo(keys[pq[j]]) > 0;
    }

    private void exch(int i, int j) {
        int swap = pq[i];
        pq[i] = pq[j];
        pq[j] = swap;
        qp[pq[i]] = i;
        qp[pq[j]] = j;
    }

    private void swim(int k) {
        while (k > 1 && greater(k/2, k)) {
            exch(k, k/2);
            k = k/2;
        }
    }

    private void sink(int k) {
        while (2*k <= n) {
            int j = 2*k;
            if (j < n && greater(j, j+1)) j++;
            if (!greater(k, j)) break;
            exch(k, j);
            k = j;
        }
    }

   public static void main(String[] args) {
        // insert a bunch of strings
        String[] strings = { "it", "was", "the", "best", "of", "times", "it", "was", "the", "worst" };

        myIndexMinPQ<String> pq = new myIndexMinPQ<String>(strings.length);
        for (int i = 0; i < strings.length; i++) {
            pq.insert(i, strings[i]);
        }

        // delete and print each key
        while (!pq.isEmpty()) {
            int i = pq.delMin();
            StdOut.println(i + " " + strings[i]);
        }
        StdOut.println();
    }
}

代码讲解

成员变量
int maxN: 队列中能够存储的最大元素数量。
int n: 当前队列中的元素数量。
int[] pq: 存储索引的二叉堆，pq[i] 表示索引 i 在堆中的位置。
int[] qp: 反向索引，qp[i] 表示索引 i 在 pq 中的位置。如果 i 不在队列中，qp[i] 值为 -1。
Key[] keys: 保存优先级的数组，keys[i] 表示索引 i 对应的优先级。
构造函数

public myIndexMinPQ(int maxN) {
    this.maxN = maxN;
    n = 0;
    keys = (Key[]) new Comparable[maxN + 1];
    pq   = new int[maxN + 1];
    qp   = new int[maxN + 1];
    for (int i = 0; i <= maxN; i++)
        qp[i] = -1;
}

初始化一个最大容量为 maxN 的索引优先队列。
keys、pq、qp 数组的大小都为 maxN + 1，因为堆的实现从索引1开始。
将 qp 数组初始化为 -1，表示没有元素被插入。
isEmpty() 方法

public boolean isEmpty() {
    return n == 0;
}

判断队列是否为空，若 n == 0 则队列为空。
contains(int i) 方法

public boolean contains(int i) {
    return qp[i] != -1;
}

判断索引 i 是否在队列中，若 qp[i] != -1 则存在。
size() 方法

public int size() {
    return n;
}

返回队列中的元素数量。
insert(int i, Key key) 方法

public void insert(int i, Key key) {
    n++;
    qp[i] = n;
    pq[n] = i;
    keys[i] = key;
    swim(n);
}

将索引 i 及其对应的优先级 key 插入队列。
更新 qp[i] 和 pq[n]，并通过 swim 方法维护堆的有序性。
delMin() 方法

public int delMin() {
    int min = pq[1];
    exch(1, n--);
    sink(1);
    qp[min] = -1;
    keys[min] = null;
    pq[n+1] = -1;
    return min;
}

删除并返回优先级最低的元素的索引。
通过 exch 和 sink 方法保持堆的有序性。
删除后清理相应的 qp 和 keys 以帮助垃圾回收。
changeKey(int i, Key key) 方法

public void changeKey(int i, Key key) {
    keys[i] = key;
    swim(qp[i]);
    sink(qp[i]);
}

更新索引 i 的优先级 key，并通过 swim 和 sink 方法维护堆的有序性。
greater(int i, int j) 方法

private boolean greater(int i, int j) {
    return keys[pq[i]].compareTo(keys[pq[j]]) > 0;
}

比较 pq 中两个元素的优先级，返回 pq[i] 是否大于 pq[j]。
exch(int i, int j) 方法

private void exch(int i, int j) {
    int swap = pq[i];
    pq[i] = pq[j];
    pq[j] = swap;
    qp[pq[i]] = i;
    qp[pq[j]] = j;
}

交换 pq 中两个元素的位置，同时更新 qp。
swim(int k) 和 sink(int k) 方法

private void swim(int k) {
    while (k > 1 && greater(k/2, k)) {
        exch(k, k/2);
        k = k/2;
    }
}

private void sink(int k) {
    while (2*k <= n) {
        int j = 2*k;
        if (j < n && greater(j, j+1)) j++;
        if (!greater(k, j)) break;
        exch(k, j);
        k = j;
    }
}

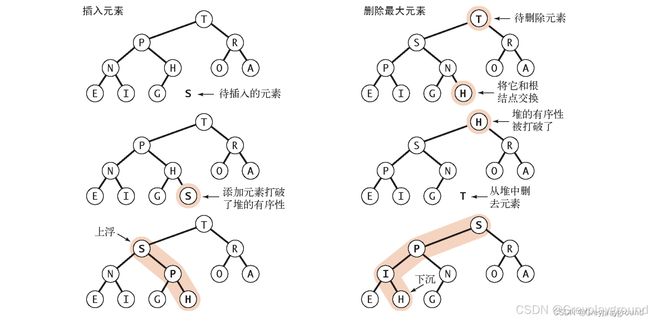
swim：用于在插入元素后恢复堆的有序性，将节点上浮到正确的位置。
sink：用于在删除元素后恢复堆的有序性，将节点下沉到正确的位置。
main 方法

public static void main(String[] args) {
    String[] strings = { "it", "was", "the", "best", "of", "times", "it", "was", "the", "worst" };

    myIndexMinPQ<String> pq = new myIndexMinPQ<String>(strings.length);
    for (int i = 0; i < strings.length; i++) {
        pq.insert(i, strings[i]);
    }

    while (!pq.isEmpty()) {
        int i = pq.delMin();
        StdOut.println(i + " " + strings[i]);
    }
    StdOut.println();
}

插入了一系列字符串，并按照优先级从高到低（即从词典顺序最小到最大的顺序）删除并打印每个元素。

总结

该代码实现了一个索引最小优先队列，支持插入、删除最小元素、更改优先级等操作，并用堆结构来高效地实现这些操作。

实验结果

C:>java myIndexMinPQ            
3 best
0 it
6 it
4 of
8 the
2 the
5 times
7 was
1 was
9 worst