第二次机器学习的作业完成了,写一下总结。
作业要求:实现用线性判别分析(LDA,LinearDiscriminantAnalysis)的二分类,用KNN比较LDA和PCA在有监督学习下的分类区别。
开题:第一眼看到题目,“用KNN比较LDA和PCA在有监督学习下的分类区别。”这句话,是我自己理解的,因为当时老师是口头布置了一下这个,板书自己没太注意,首先LDA实现二分类没什么问题,就是一正类一负类,而至于之后的用LDA和PCA分别提取特征来进行KNN,也没有多大的编码难度,这次作业的代码算是比较顺利得完成了。
实作过程:码量小,简单(很多操作,例如矩乘,求(伪)逆就调包实现了),画了一下准确度的图(Y:准确度,X:n_component,LDA和PCA同图对比)。
踩坑记录:这么简单的作业我会踩坑?踩哭了,一开始不知道矩阵还有伪逆,直接求LDA的Sw矩阵的逆,一直报错Sw是奇异矩阵(Det=0,无逆),最后询问了zxg同学,才了解到有个伪逆,求完伪逆就顺顺利利得完成了LDA部分。伪逆有复数复数复数(实数域无解了),然后也丢进去算了欧氏距离,竟然没有什么差错。。此外,我的W矩阵,竟然变成了一个tuple,而之前的矩阵shape都是正确的,在求完伪逆,取完前目标个特征向量之后,W竟然变成了tuple???而最诡异的是,当我调包LDA的时候,库函数的矩阵是实矩阵,而且二分类的效果碾压我自己写的,有点不服,都是个LDA,为什么库函数这么优秀,关键是多分类的时候为什么没有复数?对此,xg同学采用的是保证W可逆求逆,而我是求伪逆,均出现了复数,实属摸不着头脑,疑惑在于为何库函数没有求出复数?至于KNN部分,就是一个暴力过程,在此并不赘述。
LDA公式:二分类时:$S_b = S_t - S_w$ ; 多分类时:$S_b = ( \mu_0 - \mu_1) * ( \mu_0 - \mu_1 )^T$
LDA和PCA的n_component参数的学习:确实理清了一些之前很模糊的概念。
首先:LDA的n_component最大值只能是类-1(例如一共有10个类,n_component的最大值就是10-1=9),不可以超过这个值,为什么?因为每个类的类间散度矩阵的秩都是1,一共C个类,所以是C,但是总体有一个线性相关,所以是C-1(即无关组的大小是C-1)。通俗理解,就像是概率论的自由度,或者说组原的公操作。
其次:PCA,PCA的本质是组成成分分析,按照我的理解来说,就是拆成基向量(通俗解释),显然有几个基向量是非常重要的(比如笛卡尔坐标的XOY,空间的XOYOZ),拆到了几个关键的,甚至就不需要别的了(以免浪费时间、空间),这点来说很像一个矩阵的奇异值分解(方阵的话,就是我们熟知的特征值特征向量)。所以,PCA的n_component只要比原本的维度低,我觉得就可以,当然低个1、2维就太没意思,怎么也要压成1、2维。(有点夸大)
学习记录:第一次作业的sift,反向优化之后询问了老师,得到的回答是32x32的灰度图太简单了,太简单了(……)所以sift适合提取复杂一点的,所以变成了反向优化。说实话,我觉得我自己写的python代码还是有种cpp的感觉,看了zxg同学(wsxgxmd(我是xg小迷弟))所谓的“基操”,就好像问hhd同学(wshdxmd)算法回答“基操”一般,为何别人总是这么秀,我也想这么秀,2333。不得不说,还是杰哥(jgtxdy!)真诚,呜呜呜。
思考:上面的插科打诨结束了,说点最近的感受。1、专心很重要,事情是很多的,专心是很难的,但是专心了肯定做得不会差。2、心态很重要,差异一定是存在的,需要接受现实,但不可以安于现状。3、多思索,多思索,多思索。想深了,学深了总是对提升有很大帮助的。
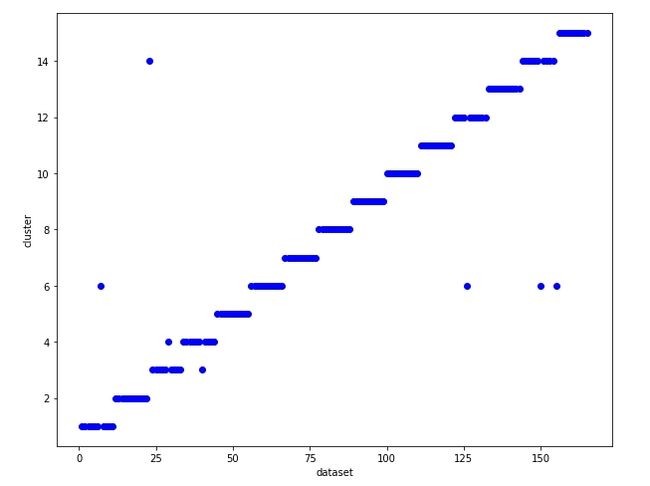
图:(代码忘了加这个,来补一下)
Yale_32x32(X:每个样本的下标,Y;每个样本被预测的类)
PS:不奶杰哥和hd了,以免周末他们键盘冒奶。希望有一天我也能笑黄巢。