谈谈集成学习
声明:本文档撰写过程中,参考过其他博文,如盗用过2张图,由于文章久远,就不特别说明出处了,如有侵权,可以联系删除或者作出说明。
1概念
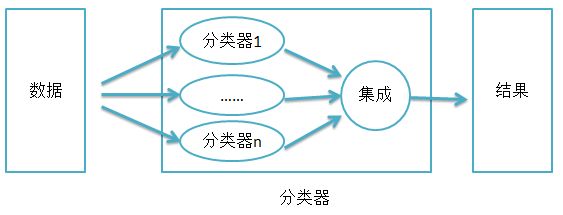
集成学习(Ensemble Learning)指将多个弱分类器构成一个强分类器。跟一般分类算法比,集成学习获得的分类器其精度比较高。
其思想可表达如下
【数据】
相比于其他分类算法,集成学习对于数据集过大或过小的情形有妙用!
数据集较大时,可以分为不同的子集,分别进行训练,然后再合成分类器。
数据集过小时,可使用自举技术(bootstrapping),从原样本集有放回的抽取m个子集,训练m个分类器,进行集成。
此外,如果数据可以(人工)分为不同类别的训练集,需要分开训练(可能不同训练集抽取的特征也不一样),这时候也需要集成学习。(下文中的嫁接法可能是将人工分类别变为模型分类别,即把数据的分类别做到了极致。)
【弱分类器】
不同弱分类器可以是不同的算法,也可以是同一个算法但是参数不一样。另外,一般要求每个弱分类器的错误率不能高于0.5。(高于0.5可以舍去。)
【集成】
集成的方法大概有以下几种
1选择n个分类器中最优的那个,注意通过测试集的验证,防止过拟合。
2投票法,即纯加法模型(bagging)
3逐步的线性组合(即逐步的加权求和,权在每个分类器产生后已经定下。boosting)
4使用模型(stacking)
2常见方法
集成学习常见方法有3种,分别是Bagging(装袋法)、Boosting(提升)、Stacking(堆叠)。此外再放一个嫁接的思想,但是目前还是大概的感觉。
2.1Bagging
Bagging是Bootstrapaggregating的缩写。其思想是,在原始样本中随机抽取子集,用不同子集训练基分类器,最后对每个基分类器求平均(投票),获得最终的分类器。
注0、Bagging训练模型可以并行。
注1、随机获取样本子集的方法有很多种,最常用的是有放回抽样的booststrap,也可以是不放回的抽样。
注2、基分类器可以是相同的模型,也可以是不同的,一般使用同一种,最常用的是决策树。
注3、由于bagging提供了一种降低方差(variance)的方式,所以一般会使用比较强、复杂的基分类器模型(比如完全生长的决策树模型);作为对比,在boosting方法中会使用非常弱的基学习器模型(比如不完全生长的决策树模型)。
RF(随机森林)就是在Bagging中使用CART(DT的一种)。
RF中基学习器使用的是CART,由于算法本身能降低方差(variance),所以会选择完全生长的CART树。抽样方法使用bootstrap,除此之外,RF认为随机程度越高,算法的效果越好。所以RF中还经常随机选取样本的特征属性、甚至于将样本的特征属性通过映射矩阵映射到随机的子空间来增大子模型的随机性、多样性。RF预测的结果为子树结果的平均值。RF具有很好的降噪性,相比单棵的CART树,RF模型边界更加平滑,置信区间也比较大。一般而言,RF中,树越多模型越稳定。
2.2Boosting
Boosting的思想是,逐步地、串行地获得一个一个的分类器,然后把他们以带权加法形式组装在一起协同工作。所谓串行,指下一次的训练会受到上次的训练的分类器影响。(所以Boosting不易并行化。)
Boosting下面,更为细化的方法有AdaptiveBoosting(AdaBoost)和Gradient Boosting,但是它们仍是两种算法框架,而非基算法。
Boosting的思想是,对一份数据,不断根据上次的分类器效果调整数据的权重,依次建立M个模型(分类器),最终对M个分类器加权组合得到的最终的分类器。
注1:一般地,每个模型比较简单,称为弱分类器(weak learner)。
注2:调整权重的方法是,将上一次分错的数据权重提高一点,分对的数据权重可以降低或者不变。
其思想可以用下图形象地表示:
细节请见笔记(哈哈,目前还在草稿纸上)。
2.3Stacking
Stacking的思想是,首先我们训练多个不同的模型,然后以这些模型的输出(Y)为输入(自变量X)、以样本正确的标记为因变量Y,通过选择一个分类算法(暂且称之为组合算法)来训练一个模型,得到最终的分类器。如果可以选用任意一个组合算法,那么理论上,Stacking其实可以表示各种集成方法。然而,实际中,我们通常使用单层logistic回归作为我们的组合算法。
其思想可表达如下
注1:n个训练集采用n折交叉验证,及利用n-1个训练集作为训练数据,其中一个训练集作为测试数据。
注2:最终的那个训练集,其X变量是n个分类器的分类结果,其Y变量是真实标签。
【open】2.4嫁接
这块内容目前只接触到一个词,还没形成系统的知识。但是脑海中有一副场景,觉得很有潜力,所以暂时先记下。听到过的有DT+LR,GBDT+LR。
大概的思想是,数据先经过一棵不完全的树,对数据进行粗略的分类,到了叶子节点后,再进行一个线性模型(如LR)。
3附录
3.1抽样方法bootstrap
Bootstrapping 自举技术(或叫自助技术),它是一种对数据集D进行重复抽样(即放回式抽样)的方法。其统计背景、意义不在此展开。
3.2模型的Variance和Bias
一个模型,其效果应该体现在测试集上,即看重模型的泛化能力。泛化能力用来衡量“模型在大量测试数据上的表现能力”。
=====插曲-begin=======
对于训练集和测试集的效果,有如下讨论
如果(测试集,训练集)=(好,好)则说明模型好,其泛化能力好;
如果(测试集,训练集)=(好,不好),那说明模型过拟合,其泛化能力不好;
如果(测试集,训练集)=(不好,*),那说明模型欠拟合,理论上其泛化能力当然更不好。
很多时候,我们的模型要么过拟合、要么欠拟合,这叫我们需要找到一个平衡点,做一个折中(trade-off)。
=====插曲-end=======
偏置-方差分解(Bias-Variance Decomposition)是统计学派看待模型效果(模型泛化能力)的一种度量,但是其实用价值不大(Bagging也许是一个例外),因为这种度量是建立在多个数据集的,而实际中只会有一个训练数据集,将这个数据集作为一个整体进行训练会比将其划分成多个固定大小的数据集进行训练再取平均的效果要好。
所以我们就简单的给出一些定性的说法。在进行学习时,就会存在偏置和方差之间的平衡。复杂的模型(如次数比较高的多项式)会有比较低的偏置和比较高的方差,而比较简陋的模型(比如一次线性回归)就会得到比较高的偏置和比较低的方差。
简单来说,
Bias过大,Variance过小,是模型过于简单,导致欠拟合。
Bias过小,Variance过大,是模型过于复杂,记住了太多细节,包括噪音,导致过拟合。
理解:方差,体现模型对待不同样本的差异性。方差过大,表示照顾了太多细节,引入过多因素(从而需要更多参数),过分体现样本的差异。