DFT基础
离散傅立叶变换是个什么东西?一句话:就是离散周期信号的傅立叶级数展开。
我用的教材(东南管致中编信号系统第五版)里面绕了一个大圈,从拉普拉斯变换跑到z变换,再从z变换推到离散傅立叶变换。这实际上反而把简单问题复杂化了。
傅立叶变换里面有一句很坑爹的“口诀”,叫周期对离散,离散对周期。周期离散信号的频谱是离散周期的。
乍一看这个没什么问题。问题就出在“离散”这两个字上。傅立叶变换和离散傅立叶变换的区别也就在这两个字上。
傅立叶变换其实是一个“瘸腿”的玩意。一般是从傅立叶级数开始导出傅立叶变换的。傅立叶级数很漂亮,物理意义相当清晰。它表示一个周期信号可以用一族正交完备的正弦波通过线性组合得到。这些正弦波的幅度大小如下计算:
傅立叶级数建立了时域和频域之间一一对应的关系。时间函数的傅立叶展开不是抽象的,而是实实在在的。因为知道了傅立叶级数,就可以还原出原始波形。
![]()
对于周期函数,傅立叶级数展开有明晰的物理意义。这是因为周期信号的特征是:周期。这就意味着信号的能量是无限的。而合成这个信号用的无穷多个正弦波,其能量也是无限的。只是高次谐波占据的能量比例很小,所以用有限的几个谐波就能得到很好的工程近似。
对于一般的连续函数。如果不视为时域有限而进行周期延宕的话,就把它视为周期无穷大去处理。但这样一来造成一个要命的问题:因为![]() 的表达式分母上是除以周期的,所以一旦视为无穷大,对有限能量信号,就带来了
的表达式分母上是除以周期的,所以一旦视为无穷大,对有限能量信号,就带来了![]() 的问题。所以傅立叶变换里面把
的问题。所以傅立叶变换里面把![]() 又乘了回去。
又乘了回去。
这个乘回去的操作其实一样要命:对于有限能量信号,事情好办了;对于无限能量信号,比如![]() ,这样又玩不下去了。因为积分后不去除以
,这样又玩不下去了。因为积分后不去除以![]() ,
,![]() 变成了无穷大。
变成了无穷大。
当然我们不允许这种事情出现。所以有了Dirac(![]() )函数和Laplace变换。Laplace变换是用一个随时间衰减的
)函数和Laplace变换。Laplace变换是用一个随时间衰减的![]() 的信号把那些随时间增长的信号给“拉回来”。而
的信号把那些随时间增长的信号给“拉回来”。而![]() 函数是用来解决
函数是用来解决![]() 这类“等幅振荡”的信号。
这类“等幅振荡”的信号。
![]() 是一个很关键的角色。它不是一个实际存在的函数。而是为了解决这套数学工具自洽性缺陷而人为引入的一个定义。所以这个函数有几个很厉害的特点,把那些要命的问题都给搞定了。
是一个很关键的角色。它不是一个实际存在的函数。而是为了解决这套数学工具自洽性缺陷而人为引入的一个定义。所以这个函数有几个很厉害的特点,把那些要命的问题都给搞定了。
这是一个很bug的定义。有了这个定义,结合傅立叶变换的时移特性,就得到了一般正弦函数的傅立叶变换,比如
![]() 即频域上的两个左右对称的
即频域上的两个左右对称的![]() 函数(单边谱对应正半轴)。
函数(单边谱对应正半轴)。
这一定义说明:合成周期信号用的“基底函数”,即正弦波,对应的傅立叶变换是![]() 。
。![]() 应该具有什么样的特点呢?首先它应该是无穷大的。因为傅立叶变换里面是把分母上的的时间给消掉了的。其次它具有“基底”的特点,也就是任何信号既然时域上能够用正弦波来表达,那么频域上一定也是能够用
应该具有什么样的特点呢?首先它应该是无穷大的。因为傅立叶变换里面是把分母上的的时间给消掉了的。其次它具有“基底”的特点,也就是任何信号既然时域上能够用正弦波来表达,那么频域上一定也是能够用![]() 来描述的。
来描述的。
第二点:有了第一点,任何周期信号也可以进行傅立叶变换得到它们的频谱了。变换方法就是把周期信号先展开成傅立叶级数。再做傅立叶变换。因为傅立叶级数每一项就是正弦波,正弦波的频谱是![]() 函数,所以周期信号的频率也就是一系列
函数,所以周期信号的频率也就是一系列![]() 函数。因为傅立叶级数是离散的,
函数。因为傅立叶级数是离散的,![]() 函数只在基波和谐波上面有取值。所以叫“周期对离散”。
函数只在基波和谐波上面有取值。所以叫“周期对离散”。
第三点:对于冲激序列,也就是等间距的、无限长的![]() 函数,其傅立叶变换为:
函数,其傅立叶变换为:
这是另一个很厉害的性质。也是“离散对周期”的来源。这个式子的数学推导教材上有。它表明时域上周期的![]() 函数对应频域上周期的
函数对应频域上周期的![]() 函数,且频域上的频率间隔恰好等于时域的频率。
函数,且频域上的频率间隔恰好等于时域的频率。
根据这点,可以想见,因为傅立叶变换里面很重要的一个特性是卷积和乘法的对偶。所以如果用一个冲激序列去作用于一个信号,那么这个信号的频谱在频域上会被搬运到各个冲激对应的频谱上。就造成了周期的频谱。这个过程也称为“采样”。由此得到的一个著名定理就是奈奎斯特采样原理:采样频率必须是信号带宽的2倍以上才能避免混叠。
以上是教材的回顾,下面开始正题。
问题是,按照这个公式,所谓的“采样”,物理中存在吗?
不存在!不存在!不存在!
因为支撑这一特性的数学是:采样信号=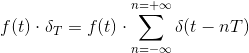 。而
。而![]() 函数不是实际的函数,所以上述的采样过程是物理不实际的。换句话说,上面图里面的“离散信号”,并不是你真正看到的信号的样子。
函数不是实际的函数,所以上述的采样过程是物理不实际的。换句话说,上面图里面的“离散信号”,并不是你真正看到的信号的样子。
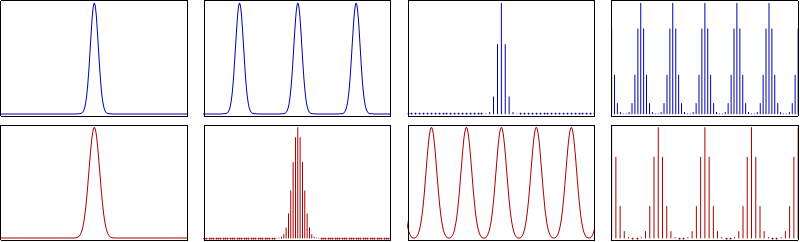
那么这张图是不是错的呢?它不是错的。但带有很强的误导性。会让人以为:实际离散周期信号的傅立叶变换得到的频谱是周期离散的。这句话是错的。其准确表述是:实际的离散周期信号的离散傅立叶变换得到的是周期离散谱。
所谓实际离散周期信号,就是实际的一组采样数据,可以被计算机处理的数据,比如每隔四分之一个周期测到的正弦波值:0,0.7,1,0,-0.7,……
对于一个实际的离散周期信号,如果我们去做傅立叶变换,会发现一个尴尬的事情:因为积分值只在某几个点上取,所以这个东西压根没法去算。但物理上我们可以想像,既然你的信号是一个连续波形去采样得到的,那么用原来的连续波形的傅立叶展开去采样,肯定也能得到一样的结果。所以,我们何不直接去对这个信号去做傅立叶变换呢?假定我们用的原始信号是![]() ,注意它是一个周期信号,假设周期为
,注意它是一个周期信号,假设周期为![]() 。我们在每个周期内做
。我们在每个周期内做![]() 点采样,注意这
点采样,注意这![]() 点是等间距的。这个事情是对
点是等间距的。这个事情是对![]() 函数的一个近似,但是实际的。因为采集信号在某一时间的数据并记录下来完全没有问题。这样就得到了一个离散周期信号
函数的一个近似,但是实际的。因为采集信号在某一时间的数据并记录下来完全没有问题。这样就得到了一个离散周期信号![]() 。对它进行傅立叶级数展开:
。对它进行傅立叶级数展开:
这个式子本身也没法计算,因为![]() 是离散的。所幸利用黎曼积分的定义,可以用梯形面积的累加来代替积分。所以有
是离散的。所幸利用黎曼积分的定义,可以用梯形面积的累加来代替积分。所以有
考查一下这里的![]() 和
和![]() ,
,![]() 表示时间刻度,
表示时间刻度,![]() 表示采样的时间间隔,显然有
表示采样的时间间隔,显然有
代入上面的式子,得到:
这里,奇异的事情出现了:首先,原始信号的周期![]() 在消失了。这就说明周期信号一旦做了离散处理以后,原来的周期信息不再重要。其次,原来连续信号的傅立叶级数的基频
在消失了。这就说明周期信号一旦做了离散处理以后,原来的周期信息不再重要。其次,原来连续信号的傅立叶级数的基频![]() ,在这里“消失”了,“基频”变成采样点数量也就是采样频率:
,在这里“消失”了,“基频”变成采样点数量也就是采样频率:![]() 。第三,
。第三,![]() 的指数上出现了两项:
的指数上出现了两项:![]() 。
。![]() 反映采样的数目,
反映采样的数目,![]() 对应“谐波”。最后,整个式子的系数是
对应“谐波”。最后,整个式子的系数是![]() 。
。
仔细去审查这个式子,不难理解,![]() 和
和![]() 是有关联的。因为采样点越多,每个区间的间隔就越小,梯形就越“窄”。比较有意思的是
是有关联的。因为采样点越多,每个区间的间隔就越小,梯形就越“窄”。比较有意思的是![]() 。按照原来的思路,
。按照原来的思路,![]() 可以取负无穷到正无穷的任意一个整数,或者说谐波分量是有无穷多个的。这里面
可以取负无穷到正无穷的任意一个整数,或者说谐波分量是有无穷多个的。这里面![]() 依然可以取遍所有整数,但表现出了周期性。即
依然可以取遍所有整数,但表现出了周期性。即![]() 的值和
的值和![]() 是一样的。
是一样的。![]() 是周期函数。
是周期函数。
由于![]() 在表达式里面不体现。所以用周期序列
在表达式里面不体现。所以用周期序列![]() 来表示采样信号。对周期采样信号
来表示采样信号。对周期采样信号![]() ,其离散傅立叶变换即定义为:
,其离散傅立叶变换即定义为:
由上面的推导,不难看出,离散傅立叶变换本质就是离散信号的傅立叶级数展开,只不过求和代替了积分。所以这个变换和傅立叶变换的不同就体现在它是实际可以进行物理操作的。而且可以明显地看到,采样点越多,求和值越接近积分,也就意味着得到的波形更精确。另外,由于![]() 都是以
都是以![]() 为周期的,所以一个周期里有多少个采样点,就有多少根谱线。
为周期的,所以一个周期里有多少个采样点,就有多少根谱线。
另外,![]() 的周期性其实是基于离散特性的。也就是说,比如每隔1秒去采样,那么
的周期性其实是基于离散特性的。也就是说,比如每隔1秒去采样,那么![]() 和
和![]() ,
,![]() ……得到的值没有区别。因为都是采集到过零点的值。所以对离散信号,我最终得到这个谐波频率取决于我的采样频率,而不在于信号本身。假设一个周期信号固定地在每个周期的某一时刻有一个剧烈的跳跃,但采样信号捕捉不到。那么我用DFT计算得到的这组信号线性叠加后得到的信号和原始信号比是损失了高频成分的。但能保证在采样点上值的一致。(类似于数值分析里的插值)
……得到的值没有区别。因为都是采集到过零点的值。所以对离散信号,我最终得到这个谐波频率取决于我的采样频率,而不在于信号本身。假设一个周期信号固定地在每个周期的某一时刻有一个剧烈的跳跃,但采样信号捕捉不到。那么我用DFT计算得到的这组信号线性叠加后得到的信号和原始信号比是损失了高频成分的。但能保证在采样点上值的一致。(类似于数值分析里的插值)
最后回看一点:表达式里面的![]() 没了,是不是意味着对DFT,可以处理任意周期信号了呢?或者说信号的周期没有意义了呢?
没了,是不是意味着对DFT,可以处理任意周期信号了呢?或者说信号的周期没有意义了呢?
并不是!
因为![]() 其实和
其实和![]() 关联:
关联:![]() 。对于任何一个实际系统,如果采样间隔即采样频率一定,显然
。对于任何一个实际系统,如果采样间隔即采样频率一定,显然![]() 越大,
越大,![]() 就能越多。
就能越多。
从这一点上也更加体现了奈奎斯特采样定理的作用:以原始信号带宽的两倍去采样,再进行DFT时,DFT的信号基频是原始信号的两倍,所以高频分量不会有任何损失。甚至比原始信号更细致平滑。但DFT合成出来的信号和原始信号绝对不是同一信号,而只是保证采样点的一致性。
DFT逆变换IDFT也很容易写出:
应该说,DFT才是真正实用的操作。当然更实际的是FFT。而傅立叶变换更多地侧重于理论分析的作用。可惜的是当初上课只讲到了Z变换。现在研究![]() 调制还要回头补课。
调制还要回头补课。
——————————————————————————————————————————————————
更新:2018/9/11
今天问了老板一个问题,就是论文里面用![]() 给采样信号建模准不准确?
给采样信号建模准不准确?
回答如下:矩形信号频域包络是sin(x)/x,信号宽度越窄,相当于包络展宽、变平了。![]() 就是极限的情况。
就是极限的情况。
恍然大悟:论文里面强调系统的低通滤波特性,意味着![]() 建模后滤波得到的近似和实际矩形的结果相近。
建模后滤波得到的近似和实际矩形的结果相近。
所以采样系统能不能用![]() 建模取决于系统频响特性。老板赛高!
建模取决于系统频响特性。老板赛高!

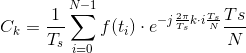
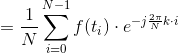
![X_K=\frac{1}{N}\sum_{i=0}^{N-1}x[i]\cdot e^{-j\frac{2\pi}{N}k\cdot i}](http://img.e-com-net.com/image/info8/9c8bb852a17b4cdf9b375f0f18b00bec.gif)
![x[i]=\sum_{k=0}^{N-1}X[k]\cdot e^{j\frac{2\pi}{N}k\cdot i}](http://img.e-com-net.com/image/info8/f8c10639ac0d44ddbcbc8012c2390c86.gif)