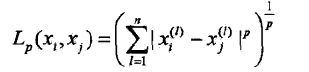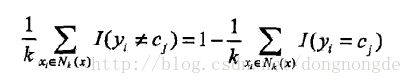k近邻法(K-NN)
K近邻法(k-NN)是一种基本的分类和回归方法。
1 K近邻法——分类
已知:训练数据集,数据集中的每一个实例由一个特征向量表示,并且显示的给出了该
实例所属的类别。
输入:一个新实例的特征向量,参数k的数值。
输出:输入实例所属的类别。
设训练集
T = { (x1,y1) , (x2,y2),...,(xN,yN) }
其中,N为训练样本个数,i = 1,2,...,N, xi为表示第i个训练样本的特征向量,yi为其对
应的类别(类别的个数与样本个数没有直接联系)。
根据给定的距离度量(如欧式距离),在训练T中找出与输入实例x距离最近的k各点,
将这k个点的集合记为Nk(x)。直观来看Nk(x)对输入实例x属于哪个类别是最有发言权的,
这也是k近邻法简单却没放弃准确度的原因。
分析Nk(x),利用分类决策方法(如多数表决法)决定x属于哪个类别。
其中I为指示函数,当yi= cj是I为1,否则为0。
该式的含义为在Nk(x)中,哪种类别占的最多则输入实例属于哪一类,这是最简单的分类
决策方法,也可将Nk(x)中每个实例赋予一定的权值进行分类决策,这种方法对于一些类
别容量差别较大的情况效果较好。
1.1 距离度量
特征空间两个实例点的距离表示了他们的相似程度。K近邻法中使用的是欧式距离,同
样可以使用其他距离。
上标(m) 表示向量第m维的数值。
则一般距离Lp定义为:
当p=2时就是我们常用的欧式距离。
1.2 k值的选择
k值的选择会对k近邻法的结果产生重大的影响,若选择较小的k值,学习的近似误差会
减小( 因为k值越小则选出的实例整体越接近输入实例 );但学习的估计误差会增大( 这
种情况下容错性比较小,若近邻的实例恰巧是噪声则预测往往会出错)。此种情况模型
比较复杂容易发生过拟合。
若选择较大的k值,则学习的近似误差会增大,学习的估计误差会减少。此时模型比较
简单(举个极端的例子,当k为无穷大时所有的新输入实例都在同一类,此时模型最简单)。
1.2.1 k值与模型的复杂度
1.3 分类决策规则
要使误分类率最小即经验风险最小,就要使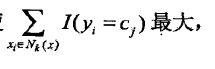 所以多数表决规则等价于
所以多数表决规则等价于
经验风险最小化。
2 K近邻法——回归
KNN算法不仅可以用于分类,还可以用于回归。通过找出一个样本的k个最近邻居,
将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。更有用的方法
是将不同距离的邻居对该样本产生的影响给予不同的权值(weight),如权值与距离成正比。
参考文献:统计学习方法(李航)
ps:最近接触的机器学习领域,敬请广大读者随时不吝批评指正,感谢。