后缀自动机学习小记

简介

后缀三姐妹：后缀数组，后缀自动机，后缀树。
后缀自动机：Suffix Automation，也叫SAM。
创立算法的思路来源：能不能构出一个自动机（本质就是一个有向图），能识别一个串的所有后缀。

识别所有后缀基础想法

把所有的后缀都放进一个trie里面，比如串aabbabd。

这样的状态太多了，怎么把状态数缩小。

减小状态数的方法

定义一个子串的right集合为这个子串在原串中出现的右端点集合。
如果两个子串A和B的right集合完全相同的话，那么他们明显一个是另一个的后缀，假设A是B的后缀，那么他们再继续扩展都只会是同一种状态，所以可以把他们合并为同一种状态。
其实后缀自动机就像是一个维护right集合的关系的一个自动机。
怎么处理呢？下面会说。先看一些重要的变量。

重要的变量

先放个图。

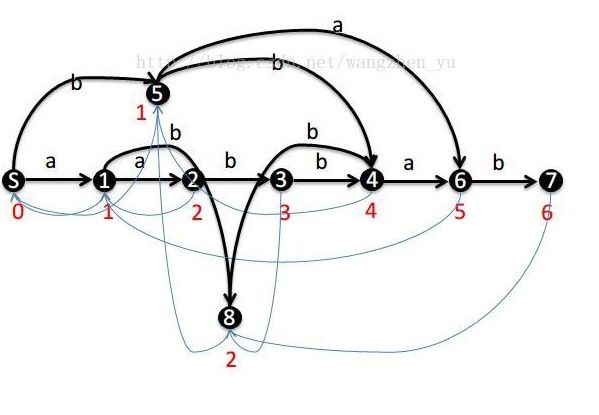
这个就是aabbab的后缀自动机。
标有数字的是状态节点。
设S状态（节点）为初始状态，表示一个空串。S节点到达任意一个节点的任意一条路径都可以形成一个字符串，且这个字符串与其他形成的字符串不同。
每个点都有一些值：len,fa,son[26]。（这里的字母都只考虑小写字母,用0…25表示小写字母）
$\bullet$1先来看看len是什么：观察上面的图，每个节点的len是这个状态（节点）表示的最大字符串的长度，一个状态表示的所有字符串就是S到达这个节点形成的所有字符串。上图中的len[0…8]=0,1,2,3,4,1,6,7,2。
$\bullet$2再来看看son[26]是什么：从一个节点x走c字符，走到了节点y，那么son[x][c]=y。但是为什么son[x][c]只连向y这个点不连向其他的点？这样连有什么性质吗？回顾上面的《减小状态数的方法》，如果两个状态的right集合相同那么可以合并为一种状态，现在这里的x状态表示的所有字符串加了个c之后right集合和y的right集合完全一样，所以son[x][c]=y，就相当于把两个状态合并了。观察上面所有节点，每个节点可能会有好几条连向来的边，这样导致这个节点会表示好多字符串，但是这些字符串的right集合都是一样的。
$\bullet$3网上很多都说的是这个节点可以接受新的后缀，fa[x]返回上一个可以接受新后缀的节点，怎么都看不懂？后来直接去看论文才搞懂。其实fa[x]的right集合是包含x的right集合的且要保证fa[x]的right集合尽量的小。因为right集合尽量小就与x的right集合更接近，如果x向后扩展出一个新的字符构成的状态y（新的后缀），fa[x]的right集合因为包含x的right集合，那么fa[x]也可以扩展出这个新的字符并构成新的状态，这个状态可能会与y合并，这就是下面要讲的后缀自动机的构造。

parent树的一些性质

$\bullet$1：从叶子节点向上走就是right集合不断合并的过程
$\bullet$2：设一个状态最短串为mins，最长串为maxs=lens，那么mins-1=max_fa[s]
$\bullet$3：网上说的接受后缀，其实可以换一种好理解的说法，parent的树从下到上right集合不断变大其实就是不断寻找后缀的过程

后缀自动机的构造

当前字符串S构建了i-1个点。
设表示S[1…i-1]的节点是last，现在要构建第i个节点，建出新的状态np，那么很明显len[np]=i=len[last]+1。设p=last

    p=last,np=++num;
    t[np].len=t[p].len+1;

那么现在要合并状态了，现在已经把p扩展出的s[i]字符的状态和np状态合并了，那么因为fa[p]的right集合包含了p的right集合，所以fa[p]扩展出s[i]这个字符的状态可能会与np合并。
什么情况下才会合并，如果son[p][s[i]]=0,那么加上了s[i]字符的状态，在当前状态的自动机下它right集合肯定只有i，因为s[i]是新出现的，所以加上新出现的right集合肯定只有i。然后fa[p]肯能也没有s[i]节点，fa[fa[p]]可能也没有s[i]，所以一直找到p=0或p有s[i]节点。

while(p&&!t[p].son[c])t[p].son[c]=np,p=t[p].fa;

为了方便，我们没有零号节点，空串用1号节点表示。
如果p=0的话，就说明已经走过了空串状态（1号节点），但是空串的right集合肯定是包括np的right集合的，所以t[np].fa=1

 if(!p)t[np].fa=1;

如果p不等于0，就说明p现在有s[i]这个节点，设p走s[i]走到的节点为q。
现在就有两种情况了
（强行把s[i]加入q可能会使t[q].len变小，而且蓝色的串不能直接放入加上X字符的集合，因为会与字符B冲突如图）：

1、t[p].len+1=t[q].len，说明p表示的最长字符串和q表示的最长字符串只差了一位（就是s字符串走到第j个得到状态p，走到第j+1个得到状态q），现在p的right集合是包含last的right集合的，但是last走s[i]字符扩展出np，p走s[i]字符扩展出q，那么q的right肯定也是包含np的right（毕竟他们字符串的起始端相同）。
2、t[p].len+1< t[q].len(t[p].len+1!=t[q].len)现在多加了一个s[i]，在这种情况q代表的串中，长度不超过t[p].len+1的字符串的right集合会多一个i超过t[p].len+1的字符串因为与p表示的最长字符串差了好几位，这些字符串的right集合可能不会增加（如上，他们的起始端不同，加了新的字符后要向两边扩展，在上面的扩展中就有B字符的冲突）。那么现在就要把状态拆开了。
新建一个节点nq，因为nq只是从q拆出来的，那么他的son和fa都是和q相等的，只是用len来拆开，len[nq]=len[p]+1。现在nq的right多了一个i，肯定包括q和np的right而且还尽量的小。
然后前面原来状态与q合并的点，他们的right集合都会多一个i，所以要他们与nq合并。
然后后缀自动机就构造完了。

else{
	    q=t[p].son[c];
	    if(t[p].len+1==t[q].len)t[np].fa=q;
	    else{
	    	nq=++num;
		    t[nq]=t[q];
		    t[num].len=t[p].len+1;
		    t[q].fa=t[np].fa=nq;
		    while(p&&t[p].son[c]==q)t[p].son[c]=nq,p=t[p].fa;
		}
	}

后缀自动机的运用

现说几个后缀自动机的性质：
1、每个状态i的点表示的字符串长度的范围是(len[fa[i]]…len[i]]。(从len[fa[i]]+1…len[i])
2、每个状态i表示的所有字符串的出现次数和right集合都是一样的。
3、由fa构成的数叫做parent树，parent树上子节点的right是父节点的子集。
4、后缀自动机的parent树是原串的反向前缀树，那么也是原串的反串的后缀树。
5、两个串的最长公共后缀是在后缀自动机上对应的状态在parent树上的lca的状态。

两个串的最长公共子串

建出A串的后缀自动机，然后B串在后缀自动机上跑。

找不同的子串的个数

方法一：用dfs处理处每个点能扩展出多少个字符串$sum[x]=\sum sum[t[x].son[i]]+1$，其实可以不用dfs，拓扑一下（按len从小到大）然后倒着做。最后sum[1]就是所有子串的个数。
方法二：$ans=\sum t[x].len-t[t[x].fa].len$，这里运用了性质1，因为节点i表示的字符串大小范围是从len[fa[i]]+1…len[i]的，那么包含不同串的个数=$len[i]-(len[fa[i]]+1)+1=len[i]-len[fa[i]]$

找第K大的子串

1、找不同串的第K大：预处理出每个状态可以构出多少个字符串，可以用dfs做，也可以对自动机拓扑一下（其实就相当于把len从小到大排序，因为len小的拓扑序也会小），然后倒着求一下（相当于DAG上的DP），然后dfs去找第K大的就好了。
2、找相同串的第K大：除了要预处理出上面的东西，还要预处理出所有状态right集合的大小（每个串在原串中出现多少次），这个会影响上面的要求的值，然后在做dfs的时候同时处理一下就好了。
原题TJOI2015弦论

求最小循环表示

最小循环表示就是这个串的所有循环串中的字典序最小的串。
把原串复制一遍到后面，然后建立后缀自动机，每次当前连出走字典序最小的点，一直走到长度为|S|为止。

找回文串

构造原串的后缀自动机，求出每个节点right集合的rmax，然后把反串放到后缀自动机上面运行，如果当前的匹配串在原串中的范围[l…r]覆盖了当前节点的rmax，那么[l…rmax]就是一个回文串。

Trie上建SAM

看起来很高级的样子，其实就是每个节点的last就是trie上的父节点。为什么要在trie上建呢？
比如说要把很多个串同时建立后缀自动机，那么有两种方法：
方法一：把所有的字符串都用一个与众不同的字符隔起来，然后建立后缀自动机。
方法二：把所有的字符串放到一个trie上，然后在trie上建立后缀自动机。（其实这个好像也叫广义后缀自动机）

总结

其实后缀数组能干的很多事情都可以用后缀自动机来干，后缀自动机因为有树形结构所以加上了树链剖分可以用很多数据结构来维护，它的代码简介，常数又小，速度又快，但是需要多加思考才能解决题目。

由于本人是一个蒟蒻

对于后缀自动机知道的也只有这么多了。

推荐题目

TJOI2015弦论
GDOI2012字符串
ZJOI2015诸神眷顾的幻想乡