详解全排列算法
简介
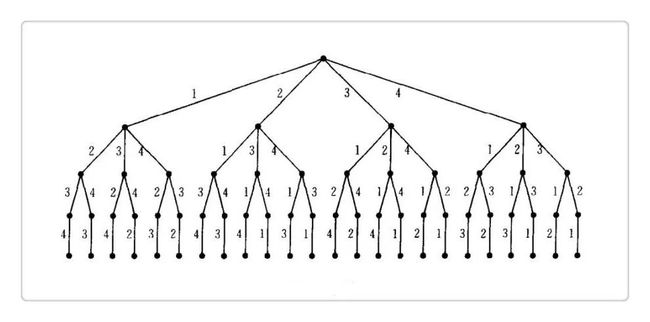
给定 {1, 2, 3, , , n},其全排列为 n! 个,这是最基础的高中组合数学知识。我们以 n=4 为例,其全部排列如下图(以字典序树形式来呈现):
我们很容易想到用递归来求出它的所有全排列。
仔细观察上图,
以 1 开头,下面跟着 {2, 3, 4} 的全排列;
以 2 开头,下面跟着 {1, 3, 4} 的全排列;
以 3 开头,下面跟着 {1, 2, 4} 的全排列;
以 4 开头,下面跟着 {1, 2, 3} 的全排列。
代码如下:
/**
*
* author : 刘毅(Limer)
* date : 2017-05-31
* mode : C++
*/
#include
#include
using namespace std;
void FullPermutation(int array[], int left, int right)
{
if (left == right)
{
for (int i = 0; i < 4; i++)
cout << array[i] << " ";
cout << endl;
}
else
{
for (int i = left; i <= right; i++)
{
swap(array[i], array[left]);
FullPermutation(array, left + 1, right);
swap(array[i], array[left]);
}
}
}
int main()
{
int array[4] = { 1,2,3,4 };
FullPermutation(array, 0, 3);
return 0;
}
运行如下:
咦~ 递归写出的全排列有点不完美,它并不严格遵循字典序。但是熟悉 C++ 的朋友肯定知道另一种更简单,更完美的全排列方法。
定义于文件
1、next_permutation,对于当前的排列,如果在字典序中还存在下一个排列,返回真,并且把当前排列调整为下一个排列;如果不存在,就把当前排列调整为字典序中的第一个排列(即递增排列),返回假。
2、prev_permutation,对于当前的排列,如果在字典序中还存在上一个排列,返回真,并且把当前排列调整为上一个排列;如果不存在,就把当前排列调整为字典序中的最后一个排列(即递减排列),返回假。
/**
*
* author : 刘毅(Limer)
* date : 2017-05-31
* mode : C++
*/
#include
#include
using namespace std;
void FullPermutation(int array[])
{
do
{
for (int i = 0; i < 4; i++)
cout << array[i] << " ";
cout << endl;
} while (next_permutation(array, array + 4));
}
int main()
{
int array[4] = { 1,2,3,4 };
FullPermutation(array);
return 0;
}
运行截图省略。输出结果正好符合字典序。
那这个 “轮子” 是怎么做的呢?(摘自侯捷的《STL 源码剖析》)
1、next_permutation,首先,从最尾端开始往前寻找两个相邻元素,令第一元素为*i,第二元素为*ii,且满足*i < *ii,找到这样一组相邻元素后,再从最尾端开始往前检验,找出第一个大于*i的元素,令为*j,将 i,j 元素对调,再将 ii 之后的所有元素颠倒排列,此即所求之 “下一个” 排列组合。
2、prev_permutation,首先,从最尾端开始往前寻找两个相邻元素,令第一元素为*i,第二元素为*ii,且满足*i > *ii,找到这样一组相邻元素后,再从最尾端开始往前检验,找出第一个小于*i的元素,令为*j,将 i,j 元素对调,再将 ii 之后的所有元素颠倒排列,此即所求之 “上一个” 排列组合。
代码如下:
bool next_permutation(int * first, int * last)
{
if (first == last) return false; // 空区间
int * i = first;
++i;
if (i == last) return false; // 只有一个元素
i = last;
--i;
for (;;)
{
int * ii = i;
--i;
if (*i < *ii)
{
int * j = last;
while (!(*i < *--j)) // 由尾端往前找,直到遇上比 *i 大的元素
;
swap(*i, *j);
reverse(ii, last);
return true;
}
}
if (i == first) // 当前排列为字典序的最后一个排列
{
reverse(first, last); // 全部逆向排列,即为升序
return false;
}
}
bool prev_premutation(int * first, int * last)
{
if (first == last) return false; // 空区间
int * i = first;
++i;
if (i == last) return false; // 只有一个元素
i = last;
--i;
for (;;)
{
int * ii = i;
--i;
if (*i > *ii)
{
int * j = last;
while (!(*i > *--j)) // 由尾端往前找,直到遇上比 *i 大的元素
;
swap(*i, *j);
reverse(ii, last);
return true;
}
}
if (i == first) // 当前排列为字典序的第一个排列
{
reverse(first, last); // 全部逆向排列,即为降序
return false;
}
}
结后语
这篇文章主要介绍了解决不重复序列的全排列问题的两个方法:递归和字典序法。
转自:刘毅
https://61mon.com/index.php/archives/197/
![]()
1.傅里叶变换就是这么简单,你学会了吗?
2.硬件缺陷还真能用软件补?一起盘点软件为硬件填过的那些坑
3.讲真,工程师是这个星球上最酷的职业!
4.你知道嵌入式C语言中各变量存储的位置吗?
5.互相鄙视的模电和数电干了一架,结局很搞笑
6.作为一个电子工程师,学会阅读Datasheet很重要!
免责声明:本文系网络转载,版权归原作者所有。如涉及作品版权问题,请与我们联系,我们将根据您提供的版权证明材料确认版权并支付稿酬或者删除内容。