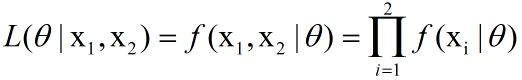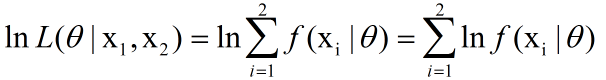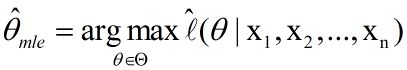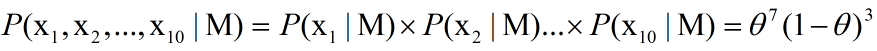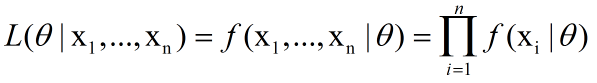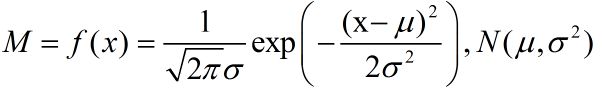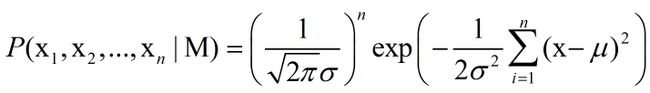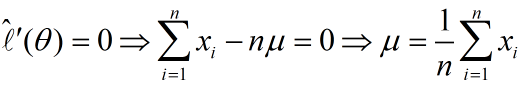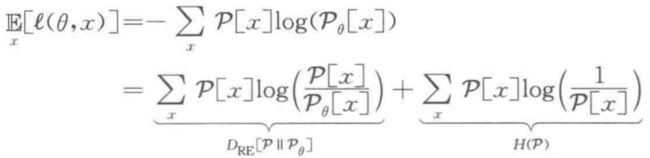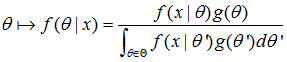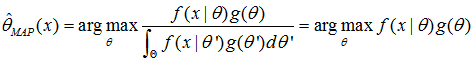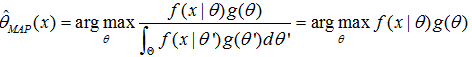1. 概率思想与归纳思想
0x1：归纳推理思想
所谓归纳推理思想，即是由某类事物的部分对象具有某些特征，推出该类事物的全部对象都具有这些特征的推理。抽象地来说，由个别事实概括出一般结论的推理称为归纳推理（简称归纳），它是推理的一种
1. 归纳推理的分类
传统上，根据前提所考察对象范围的不同，把归纳推理分为
1. 完全归纳推理：考察某类事物的全部对象 2. 不完全归纳推理：仅考虑某类事物的部分对象，并进一步根据：所依据的前提是否揭示对象与其属性间的因果联系，把不完全归纳推理分为 1）简单枚举归纳推理：在经验观察基础上所做出的概括 2）科学归纳推理：在科学实验基础上所做出的概括
这里的所谓的“对象与其属性间的因果联系”即归纳推理强度，归纳推理的强度彼此间差异很大，根据归纳强度可分为
1. 演绎推理：必然性推理 2. 归纳推理：或然性推理
而现代归纳推理的主要形式有
1. 枚举论证 2. 类别 3. 比喻论证 4. 统计论证 5. 因果论证
2. 归纳推理的必要条件
归纳推理的前提是其结论的必要条件，但是归纳推理的前提必须是真实的，否则归纳就失去了意义
3. 归纳推理的结论 - 即样本
归纳推理里的结论指的是观测到了已经发生的事物结果，具体到机器学习领域就是我们常说的样本。需要特别注意的是，前提是真不能保证结论也一定是真，有时候归纳推理的结论可能是假的，或者不完全是真的。如根据某天有一只兔子撞到树上死了，推出每天都会有兔子撞到树上死掉，这一结论很可能为假，除非一些很特殊的情况发生
0x2：枚举推理 - 不完全推理的一种
在日常思维中，人们常根据对一类事物的部分对象具有某种属性的考虑，推出这一类事物的全部对象或部分对象也具有该属性的结论，这种推理就是枚举推理，即从特殊到一般的推理过程
例如：数目有年轮，从它的年轮知道树木生长的年数；动物也有年轮，从乌龟甲上的环数可以知道它的年龄，牛马的年轮在牙齿上，人的年轮在脑中。从这些事物推理出所有生物都有记录自己寿命长短的年轮。
我们称被考察的那部分对象为样本（S），样本中某一个对象为样本个体（s），称这一类事物的全部对象为总体（A），样本属性（P），总体所具有的属性称为描述属性
枚举推理是从所考察的样本属性概括出总体属性的推理，其推理形式如下：
A 的 S 都具有 P 属性 => 所有 A 都具有 P 属性
枚举推理是典型的归纳推理，因为它体现了归纳概括这个概念的实质。从哲学的认识论意义上说，演绎体现了由一般到个别的认识过程，归纳体现了由个别到一般的认识过程，二者是互相联系、互相补充的
如果一个总体中的所有个体在某一方面都具有相同的属性，那么任意一个个体在这方面的属性都是总体的属性（普遍寓于特殊中）
例如医生为病人验血只需抽取病人血液的一小部分。母亲给婴儿喂奶只要尝一小口就能知道奶的温度，不同的个体在某方面所具有的无差别的属性称为同质性，有差别的属性称为异质性。比较而言，在科学归纳中，样本属性与描述属性具有同质性的概率较高，而在简单枚举法中，样本属性与描述属性具有同质性的概率较低
1. 全称枚举推理的批判性准则
1. 没有发现与观测结论相关的反例：只要有与结论相关的反例，无论有多少正面支持结论的实例，结论都是不真实的 2. 样本容量越大，结论的可靠型就越大：基于过少的样本所作出的概括是容易犯错误的，我们需要足够大的样本容量，也就是样本内所含个体的数量，才能确立我们对所作出的概括的信心 3. 样本的个体之间的差异越大，结论的可靠性就越大：样本个体之间的差异通常能反映样本个体在总体中的分布情况，样本个体之间的差异越大说明样本个体在总体中的分布越广。这条准则涉及样本的代表性问题 4. 样本属性与描述属性有同质性的概率越大，结论的可靠性越大：从逻辑上说，样本属性与结论所概括概括的总体属性应当具有同质性，否则就一定会有反例。对于机器学习来说，就是我们取的样本一定要是最终实际线上模型的获取方式、特征抽取提取方式等方面一定要保持一致，这样才能保证同质性
2. 特称枚举与单称枚举
在一类事物中，根据所观察的样本个体具有某种属性的前提，得出总体中的其他一些个体也具有这种属性的结论，这种推理就是特称枚举推理，例如
1. 在亚洲观察到的天鹅是白色的，在欧洲和非洲观察到的天鹅也是白色的。所以美洲的天鹅也是白的：特称枚举是从样本到样本的推理 2. 在亚洲观察到的天鹅是白色的，在欧洲和非洲观察到的天鹅也是白色的，所以隔壁小李叔叔救回来的那只受伤的天鹅也会是白的：单称推理是从已考察的样本S到未知个体
需要注意的是，上面提到的4个全称枚举的准则都同样应用于特征枚举与单称枚举，但是存在几个问题
1. 由于单称枚举和特称枚举的结论是对未知个体做出的断定，结论超出了前提的断定范围，其结论面临着更大的反例的可能性，例如小李叔叔救回来的天鹅不是白色的，或者根本就不是天鹅 2. 在日常思维实际中，单称枚举和特称枚举所推断的情况往往在未来才会出现。因而也称之为预测推理，其中单称枚举推理是最常用的形式，例如：从过去太阳总是从东方升起，推断出明天太阳也将从东方升起
0x3：完全归纳法 - 枚举推理的极限
如果前提所包含的样本个体穷尽了总体中的所有个体 ，则其结论具有必然的性质。完全归纳法的特点是前提所考察的一类对象的全部，结论断定的范围没有超出前提的断定范围，本质上属于演绎推理
0x4：概率思想和归纳思想的联系
概率思想与归纳思想之间存在密切联系。归纳法中的概率归纳推理是从归纳法向概率法发展的标志。概率归纳推理是根据一类事件出现的概率，推出该类所有事件出现的概率的不完全归纳推理，是由部分到全体的推理，其特点是对可能性的大小作数量方面的估计，它的结论超出了前提所断定的范围，因而是或然的。
从某种程度上来说，归纳是一种特殊的概率，概率方法是归纳方法的自然推广，概率是归纳法发展到一定程度的必然产物
1. 概率法 1） 概率法本身是对大量随机事件和随机现象所进行的一种归纳，是对随机事件发生的结果的归纳，它并不关心事件发生的具体过程 2）而概率方法则主要适用于多变量因果关系的复杂事件所决定的问题 2. 归纳法 1）归纳法不仅关注事件发生的结果，它还关注事件发生的具体过程，它承认事件发生过程中的规律性，并以此为基础来研究事件发生过程中的规律性 2）归纳法主要适用于少变量因果关系的简单事件所决定的问题
0x5：统计思想（数理统计）与特殊化思想的联系
特殊化思想是将研究对象或问题从一般状态转化为特殊状态进行考察和研究的一种思想方法。特殊化思想方法的哲学基础是矛盾的普遍性寓于特殊性之中。
而数理统计思想方法是通过对样本的研究来把握总体内在规律的一种研究方法，换句话说，统计是通过对特殊事物的认识来把握一般规律，因此它也是一种特殊思想方法
特殊化方法主要处理确定性问题，更侧重过程和对具体方法的把握；而统计法则主要研究随机对象，它更强调对结果和整体的把握。
数量统计思想并不局限在具体的方法层次，它主要是从思想层面来把握问题，是一种真正意义上的特殊化方法
Relevant Link:
http://www.doc88.com/p-2985317492201.html https://max.book118.com/html/2014/0104/5473598.shtm http://www.docin.com/p-355028594.html https://baike.baidu.com/item/归纳推理思想/8335575?fr=aladdin http://www.360doc.com/content/12/0312/15/7266134_193751535.shtml
2. 概率论和统计学的关系
来自于微博的一张图：
1. 概率论是统计推断的基础，在给定数据生成过程下观测、研究数据生成的性质； 2. 而统计推断则根据观测的数据，反向思考其数据生成过程。预测、分类、聚类、估计等，都是统计推断的特殊形式，强调对于数据生成过程的研究。
例如：在医院会对过去有糖尿病的所有病人进行归纳总结（建立模型，即统计归纳）；当有一个新的病人入院时，就可以用之前的归纳总结来判断该病人是否患糖尿病，然后就可以对症下药了。统计里常说的“分类”就是这个过程（即根据已知条件进行预测未来）。
统计＝样本(回顾过去的数据)归纳出总体(总结)
概率率＝总体(给定条件)对样本进行预测
统计和概率是方法论上的区别，概率是演绎（分析），统计是归纳（总结）
1. 概率论研究的是一个白箱子，你知道这个箱子的构造（里面有几个红球、几个白球，也就是所谓的联合概率分布函数），然后计算下一个摸出来的球是红球的概率（求具体条件概率） 2. 而统计学面对的是一个黑箱子，你只看得到每次摸出来的是红球还是白球，然后需要猜测这个黑箱子的内部结构，例如红球和白球的比例是多少？（参数估计）能不能认为红球40%，白球60%？（假设检验）
0x1：统计归纳合理性的理论基石 - 概率正态分布定理和概率期望定理
1. 小数定理
如果统计数据不够大，就什么也说明不了
小数定律里的“跟它的期望值一点关系都没有”，这里的期望值就是接下来要讨论的“大数定律”。2. 大数定理 - 随机变量的平均结果问题
大数定律是我们从统计数字中推测（归纳）真相的理论基础。
大数定律说如果统计数据足够大，那么事物出现的频率（统计）就能无限接近他的期望值（概率）
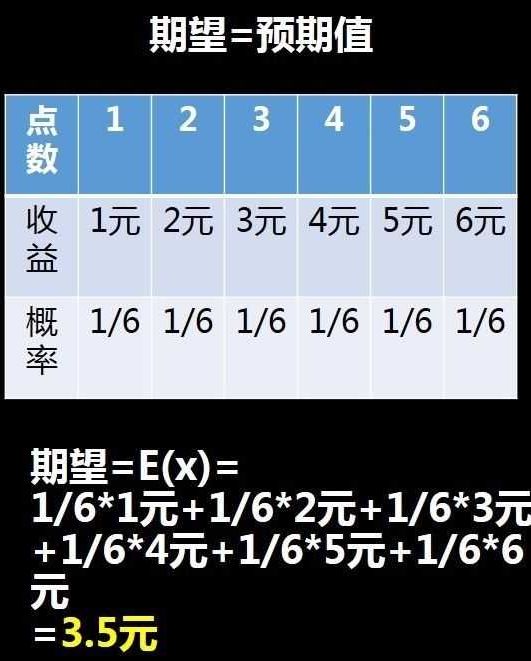
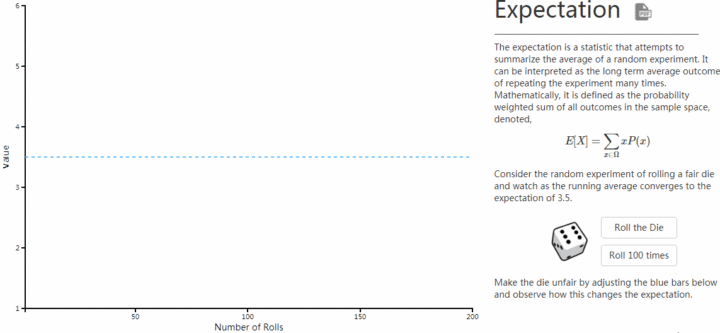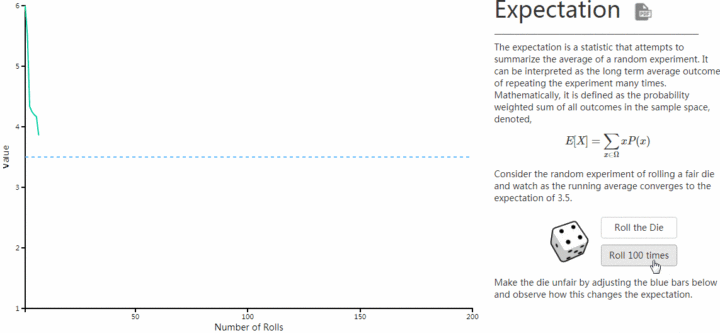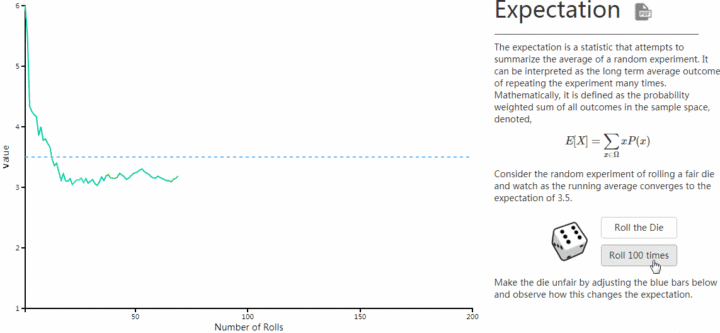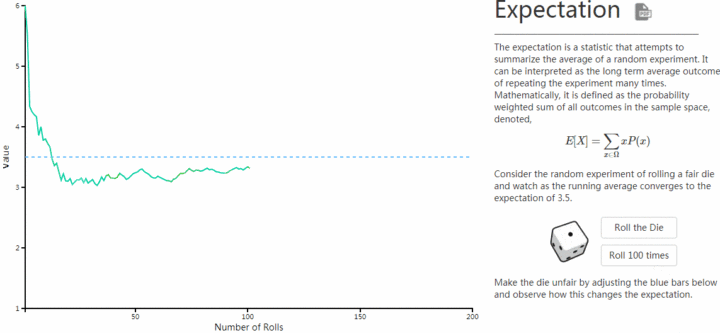
所谓期望，在我们的生活中，期望是你希望一件事情预期达到什么样的效果。例如，你去面试，期望的薪水是1万5。
在统计概率里，期望也是一样的含义，表示的也是事件未来的预期值，只不过是用更科学的方式来计算出这个数值。某个事件的期望值，也就是收益，实际上是所有不同结果的和，其中每个结果都是由各自的概率和收益相乘而来。
1/6*1元+1/6*2元+1/6*3美元）+1/6*4元+1/6*5元+1/6*6元 =3.5元
这个期望3.5元代表什么意思呢？
可能你某一次抛筛子赢了1元，某一次抛筛子赢了6元，但是长期来看（假设玩了无数盘），你平均下来每次的收益会是3.5元。
1. 我们发现当抛筛子次数少数，期望波动很大。这就是小数定律，如果统计数据很少，那么事件就表现为各种极端情况，而这些情况都是偶然事件，跟它的期望值一点关系都没有。 2. 但是当你抛筛子次数大于60次后，就会越来越接近它的期望值3.5。
3. 概率中的收敛定理 - 随机变量的概率分布问题
按分布收敛 - 中心极限定理
在一定条件下，大量独立随机变量的平均数是以正态分布为极限的。根据中心极限定理，我们通过大量独立随机变量的统计归纳，可以得到概率分布密度函数的近似值
列维-林德伯格定理
棣莫弗—拉普拉斯定理
证明的是二项分布的极限分布是正态分布，也告诉了我们实际问题时可以用大样本近似处理。0x2：为什么在大量实验中随机变量的统计结果可以归纳推理出概率密度函数？
0x3：机器学习场景中大多数是统计归纳问题，目的是近似得到概率
统计是由样本信息反推概率分布，如概率分布参数的点估计、区间估计，以及线性回归、贝叶斯估计等Relevant Link:
https://www.zhihu.com/question/19911209 https://baike.baidu.com/item/大数定律/410082?fr=aladdin https://www.zhihu.com/question/20269390 https://www.zhihu.com/question/20269390 http://blog.csdn.net/linear_luo/article/details/52760309 https://betterexplained.com/articles/a-brief-introduction-to-probability-statistics/
3. 似然函数
前面两个章节讨论了统计归纳可以推导出概率密度，以及背后的数学理论支撑基础。所以接下来的问题就是另一个问题了，how？我们如何根据一个实验结果进行统计归纳计算，得到一个概率密度的估计？根据实验结果归纳统计得到的这个计算得到的是一个唯一确定值吗？
0x1：似然与概率密度在概念上不等但是在数值上相等 - 因果论的一种典型场景
首先给出一个等式：
等式左边表示给定联合样本值
条件下关于未知参数
的函数；等式右边的
是一个密度函数，它表示给定参数下关于联合样本值的联合密度函数
从数学定义上，似然函数和密度函数是完全不同的两个数学对象：
是关于的函数，是关于的函数，但是神奇地地方就在于它们的函数值形式相等，实际上也可以理解为有因就有果，有果就有因
这个等式表示的是对于事件发生的两种角度的看法，本质上等式两边都是表示的这个事件发生的概率或者说可能性
1. 似然函数 L(θ|x)：再给定一个样本x后，我们去想这个样本出现的可能性到底是多大。统计学的观点始终是认为样本的出现是基于一个分布的。那么我们去假设这个分布为 f，里面有参数theta。对于不同的theta，样本的分布不一样，所有的theta对应的样本分布就组成了似然函数 2. 概率密度函数 f(x|θ)：表示的就是在给定参数theta的情况下，x出现的可能性多大。
所以其实这个等式要表示的核心意思都是在给一个theta和一个样本x的时候，整个事件发生的可能性多大。
0x2：概率密度函数和似然函数数值相等的一个例子
以伯努利分布（Bernoulli distribution，又叫做两点分布或0-1分布）为例：
也可以写成以下形式：
，
表示观测结果的不确定性
1. 从概率密度函数角度看
是关于参数 p 的函数，即 f 依赖于 p 的值。
对于任意的参数 pp 我们都可以画出伯努利分布的概率图，当 p = 0.5 时：f(x) = 0.5。这表明参数 p = 0.5时，观测结果的不确定性是对半开的
我们可以得到下面的概率密度图：
可以看到，参数 p 的取值越偏离0.5，则意味着观测结果的不确定性越低
2. 从似然函数角度看
从似然的角度出发，假设我们观测到的结果是 x = 0.5（即某一面朝上的概率是50%，这个结果可能是通过几千次几万次的试验得到的），可以得到以下的似然函数：
注意：这里的 π 描述的是伯努利实验的性能而非事件发生的概率（例如 π = 0.5 描述的一枚两面均匀的硬币）
对应的似然函数图是这样的：
我们很容易看出似然函数的极值（也是最大值）在 p = 0.5 处得到，通常不需要做图来观察极值，令似然函数的偏导数为零即可求得极值条件。偏导数求极值是最最大似然函数的常用方法
0x3：似然函数的极大值
似然函数的最大值意味着什么？让我们回到概率和似然的定义，概率描述的是在一定条件下某个事件发生的可能性，概率越大说明这件事情越可能会发生；而似然描述的是结果已知的情况下，该事件在不同条件下发生的可能性，似然函数的值越大说明该事件在对应的条件下发生的可能性越大。
现在再来看看之前提到的抛硬币的例子：
上面的 π （硬币的性质）就是我们说的事件发生的条件，
描述的是性质不同的硬币，任意一面向上概率为50% 的可能性有多大，
在很多实际问题中，比如机器学习领域，我们更关注的是似然函数的最大值，我们需要根据已知事件来找出产生这种结果最有可能的条件，目的当然是根据这个最有可能的条件去推测未知事件的概率。在这个抛硬币的事件中，π 可以取 [0, 1] 内的所有值，这是由硬币的性质所决定的，显而易见的是 π = 0.5 这种硬币最有可能产生我们观测到的结果。
0x4：对数化的似然函数
对数似然函数并不是一个新的概念，它只是一个具体实现上的优化做法，因为实际问题往往要比抛一次硬币复杂得多，会涉及到多个独立事件，在似然函数的表达式中通常都会出现连乘：
对多项乘积的求导往往非常复杂，但是对于多项求和的求导却要简单的多，对数函数不改变原函数的单调性和极值位置，而且根据对数函数的性质可以将乘积转换为加减式，这可以大大简化求导的过程：
在机器学习的公式推导中，经常能看到类似的转化。
0x5：概率密度函数和似然函数数值相等的另一个例子 - 掷硬币问题
考虑投掷一枚硬币的实验。通常来说，已知投出的硬币正面朝上和反面朝上的概率各自是
，便可以知道投掷若干次后出现各种结果的可能性
比如说，投两次都是正面朝上的概率是0.25。用条件概率表示，就是：
，其中H表示正面朝上。
在统计学中的大多数场景中，我们关心的是在已知一系列投掷的结果时，关于硬币投掷时正面朝上的可能性的信息。我们可以建立一个统计模型：假设硬币投出时会有
的概率正面朝上，而有
的概率反面朝上。
这时，条件概率可以改写成似然函数：
也就是说，对于取定的似然函数，在观测到两次投掷都是正面朝上时， 的似然性是0.25（这并不表示当观测到两次正面朝上时 的概率是0.25）。
如果考虑
，那么似然函数的值也会改变。
这说明，如果参数 的取值变成0.6的话，结果观测到连续两次正面朝上的概率要比假设 时更大。也就是说，参数 取成0.6 要比取成0.5 更有说服力，更为“合理”
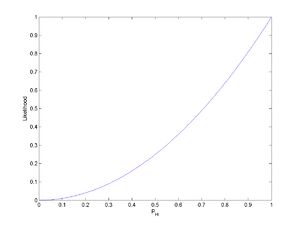
仔细思考，我们就会发现，L 是关于 PH的单调递增函数，如下图：
怎么理解这张图？即在实验结果已知的 HH 情况下，最大似然估计认为最有可能的情况是PH的概率为1，即这个硬币100%都是正面（虽然我们知道这不合理，但是反映了实验样本对似然估计合理性的影响）
总之， 似然函数的重要性不是它的具体取值，而是当参数变化时函数到底变小还是变大。对同一个似然函数，如果存在一个参数值，使得它的函数值达到最大的话，那么这个值就是最为“合理”的参数值。Relevant Link:
https://en.wikipedia.org/wiki/Maximum_likelihood_estimation https://www.zhihu.com/question/54082000 http://fangs.in/post/thinkstats/likelihood/ https://zhuanlan.zhihu.com/p/22092462 http://blog.csdn.net/sunlylorn/article/details/19610589 https://www.cnblogs.com/zhsuiy/p/4822020.html https://zhuanlan.zhihu.com/p/26614750 https://www.zhihu.com/question/48230067 https://zhuanlan.zhihu.com/p/22092462 http://fangs.in/post/thinkstats/likelihood/
4. 极大似然估计
极大似然估计是一种估计数据参数的常见统计方法，它遵循的准则是极大似然准则。极大似然准则和经验风险最小化准则一样，都是一种计算模型概率分布参数的准则，我们后面会讨论它们的区别。
0x1：从模型参数估计的角度谈极大似然估计
笔者观点：最大似然估计是利用已知的样本的结果，在使用某个模型的基础上，反推最有可能导致这样结果的模型参数值。
1. 伯努利分布下的极大似然参数估计
假设一个袋子装有白球与红球，比例未知，现在抽取10次（每次抽完都放回，保证事件独立性）。
假设抽到了7次白球和3次红球，在此数据样本条件下，可以采用最大似然估计法求解袋子中白球的比例（最大似然估计是一种“模型已定，参数未知”的方法）。
我们知道，一些复杂的问题，是很难通过直观的方式获得答案的，这时候理论分析就尤为重要了，我们可以找到一个"逼近模型"来无限地逼近我们要处理的问题的本质
我们可以定义2次实验中从袋子中抽取白球和红球的概率如下
x1为第一次采样，x2为第二次采样，f为模型, theta为模型参数，X1，X2是独立同分布的
其中theta是未知的，因此，我们定义似然L为：
L为似然的符号
因为目标是求最大似然函数，因此我们可以两边取ln，取ln是为了将右边的乘号变为加号，方便求导(不影响极大值的推导)
两边取ln的结果，左边的通常称之为对数似然
最大似然估计的过程，就是找一个合适的theta，使得平均对数似然的值为最大。因此，可以得到以下公式：
最大似然估计的公式
我们写出拓展到n次采样的情况
最大似然估计的公式（n次采样）
我们定义M为模型（也就是之前公式中的f），表示抽到白球的概率为theta，而抽到红球的概率为(1-theta)，因此10次抽取抽到白球7次的概率可以表示为：
10次抽取抽到白球7次的概率
将其描述为平均似然可得：
那么最大似然就是找到一个合适的theta，获得最大的平均似然(求最大极值问题)。因此我们可以对平均似然的公式对theta求导，并另导数为0
求导过程
由此可得，当抽取白球的概率为0.7时，最可能产生10次抽取抽到白球7次的事件。
笔者思考：
如果我们的实验结果是：前10次抽到的球都是白球，则对对数似然函数进行求导，并另导数为0，得出theta为1，即当取白球的概率是100%时，最有可能10次都抽到白球。 显然，这种"推测结果"很容易"偏离真实情况"，因为很可能是因为10次都抽到白球这种小概率事件导致我们基于观测值的最大似然推测失真，即产生了过拟合，但是造成这种现象的本质是因为"我们的训练样本未能真实地反映待推测问题的本质"，在一个不好的样本集下，要做出正确的预测也就变得十分困难。
2. 正态分布下的极大似然参数估计
我们前面说了，事物的本来规律是很复杂的，我们很难用一个百分百准确的模型去描述事物的本质，但是我们可以用一些类似的通用模型去"尽可能逼近"事物的本质。
高斯分布(正态分布)一种非常合理的描述随机事件的概率模型。
假如有一组采样值（x1,...,xn），我们知道其服从正态分布，且标准差已知。当这个正态分布的期望和方差为多少时，产生这个采样数据的概率为最大？
继续上个小节的例子：
基于n次实验观测值对参数theta预测的的似然函数
正态分布的公式，当第一参数（期望）为0，第二参数（方差）为1时，分布为标准正态分布
把高斯分布函数带入n次独立实验的似然函数中
对上式求导可得，在高斯分布下，参数theta的似然函数的值取决于实验观测结果，这和我们上例中抽球实验是一致的
笔者思考：根据概率原理我们知道，如果我们的实验次数不断增加，甚至接近无限次，则实验的观测结果会无限逼近于真实的概率分布情况，这个时候最大似然函数的估计就会逐渐接近真实的概率分布，也可以这么理解，样本观测量的增加，会降低似然函数过拟合带来的误差。
0x2：极大似然估计和经验风险最小化准则的关系
极大似然估计准则和经验风险最小化准则（ERM），是具有一定的相似性的。
在经验风险最小化原则中，有一个假设集
，利用训练集进行学习，选取假设
，实现使得经验风险最小化。实际上，极大似然估计是对于特定的损失函数的经验风险最小化，也就说，极大似然估计是一种特殊形式的经验风险最小化。
对于给定的参数
和观测样本 x，定义损失函数为：
也就是说，假设观测样本 X 服从分布
，损失函数
与 x 的对数似然函数相差一个负号。该损失函数通常被称为对数损失。
在基础上，可以验证，极大似然准则等价于上式定义的对数损失函数的经验风险最小化（仅限于对数损失函数）
这里我们可以这么理解：经验风险最小化是一种泛化的模型求参法则，它的核心是求极值。而极大似然是一种特殊的形态，即使用对数这种形式来进行极值求导。
数据服从的潜在分布为 P（不必满足参数化形式），参数的真实风险为：
其中，
称为相对熵，H 称为熵函数。
相对熵是描述两个概率分布的差异的一种度量。对于离散分布，相对熵总是非负的，并且等于 0 当且仅当两个分布是相同的。
由此可见，当
时，真实风险达到极小值。
同时，上式还刻画了生成式的假设对于密度估计的影响，即使是在无穷多样本的极限情况下，该影响依然存在。如果潜在分布具有参数化的形式，那么可以通过选择合适的参数，使风险降为潜在分布的熵。
然而，如果潜在分布不满足假设的参数化形式，那么即使由最优参数所确定的模型也可能是较差的，模型的优劣是用熵刻画的。
上面的讨论总结一下本质就是估计风险和逼近风险的概念：
1. 估计风险：我们的生成式假设是否足够逼近真实的潜在分布？ 2. 逼近风险：我们的训练样本能否支持模型得到合适的模型参数？
0x3：最大似然估计和最小二乘法的联系
线性回归中的最小二乘（OLSE）的策略思想是使拟合出的目标函数和所有已知样本点尽量靠近，本质上我们可以将拟合线（linear function）看成是一种对样本概率密度分布的表示，这样有利于我们去思考最大似然和最小二乘法在本质上的联系。
1. 最大似然估计:
现在已经拿到了很多个样本（数据集中包含所有因变量），这些样本值已经实现，最大似然估计就是去找到那个（组）参数估计值，使得前面已经实现的样本值发生概率最大。
因为你手头上的样本已经实现了，其发生概率最大才符合逻辑。这时是求样本所有观测的联合概率最大化，是个连乘积，只要取对数，就变成了线性加总。
此时通过对参数求导数，并令一阶导数为零，就可以通过解方程（组），得到最大似然估计值。
2. 最小二乘:
找到一个（组）估计值，使得实际值与估计值的距离最小。
这里评估实际值和估计值之间距离的函数就叫“损失函数”，一个常用的损失函数是平方和损失，找一个（组）估计值，使得实际值与估计值之差的平方加总之后的值最小，称为最小二乘。
这时，将这个差的平方的和式对参数求导数，并取一阶导数为零，就是OLSE。
论及本质，其实两者只是用不同的度量空间来进行的投影：
最小二乘（OLS）的度量是L2 norm distance；
而极大似然的度量是Kullback-Leibler divergence（KL散度）；
1. 一个例子说明最大似然和最小二乘区别
设想一个例子，教育程度和工资之间的关系。我们可以观察到的数据是：教育程度对应着一个工资的样本数据
1）OLS的做法
我们的目标是找到两者之间的规律，如果样本集中只有2个点，则计算是非常简单的，既不需要OLS也不需要最大似然估计，直接两点连成一条线即可。但是我们知道OLS和最大似然都是一种数学工具，它要解决的情况就是大量样本集时的数学计算问题。
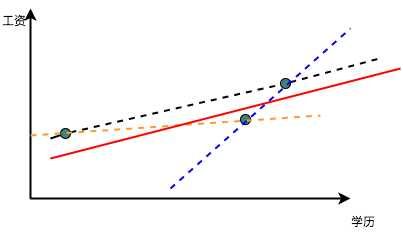
如果我们的学历-工资样本集大数量到达3个点，且这3个点不共线，那显然我们就无法通过肉眼和直觉判断直接得到linear regression function了。如下图：
如果这三个点不在一条线上，我们就需要作出取舍了，如果我们取任意两个点，那么就没有好好的利用第三个点带来的新信息，并且因为这三个点在数据中的地位相同，我们如何来断定应该选用哪两个点来作为我们的基准呢？这就都是问题了。
这个时候我们最直观的想法就是『折衷』一下，在这三个数据，三条线中间取得某种平衡作为我们的最终结果，类似于上图中的红线这样。
那接下来的问题就是，怎么取这个平衡了？
我们需要引入一个数学量化的值：误差，也就是我们要承认观测到的数据中有一些因素是不可知的，不能完全的被学历所解释。而这个不能解释的程度自然就是每个点到红线在Y轴的距离。
有了误差这个度量的手段，即我们承认了有不能解释的因素，但是我们依然想尽可能的让这种『不被解释』的程度最小，于是我们就想最小化这种不被解释的程度。因为点可能在线的上面或者下面，故而距离有正有负，取绝对值又太麻烦，于是我们就直接把每个距离都取一个平方变成正的，然后试图找出一个距离所有点的距离的平方最小的这条线，这就是最小二乘法了。
2）极大似然的做法
极大似然的估计则更加抽象一些，我们观察到了这3个点，说明这3个点是其背后“真实规律模型对应的数据集”中选出的最优代表性的3个，所以我们希望找到一个特定的底薪和教育增量薪水的组合，让我们观察到这三个点的概率最大，这个找的过程就是极大似然估计。
极大似然估计是寻找一个概率函数分布，使之最符合现有观测到的样本数据。
笔者思考：在神经元感知机算法中，求损失函数最小值（经验风险最小）寻找分界面的本质和极大似然求解是一样的，都是在寻找一个有最大概率产生当前观察样本的模型。
Relevant Link:
https://zhuanlan.zhihu.com/p/24602462 https://www.zhihu.com/question/26201440 https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence https://www.zhihu.com/question/20447622 http://blog.csdn.net/feilong_csdn/article/details/61633180 https://www.cnblogs.com/ChengQH/p/e5dd604ee211533e50187c6fd37787bd.html
5. 贝叶斯估计 - 包含先验假设（正则化）的极大似然估计
0x1：贝叶斯估计是对极大似然估计的一种改进
最大似然估计存在一定的缺陷
1. 最大似然估计属于点估计，只能得到待估计参数的一个值。但是在有的时候我们不仅仅希望知道，我们还希望知道取其它值得概率，即我们希望知道整个在获得观察数据后的分布情况 2. 最大似然估计仅仅根据(有限的)观察数据对总体分布进行估计，在数据量不大的情况下，可能不准确。
例如我们要估计人的平均体重，但是抽样的人都是小孩，这样我们得到的平均体重就不能反映总体的分布，而我们应该把“小孩之占总人口20%”的先验考虑进去。这时我们可以用贝叶斯方法。
贝叶斯估计和最大似然估计最大的区别我认为在于：
贝叶斯估计对假设空间的概率分布有一个预先的假设（先验），而不是完全无脑地信任观测样本数据，它相当于先建立一个初始基线值，然后根据观测样本值去不断修正它，这样修正后的结果具有很好的稳定性，不会随着观测样本的波动而波动。
0x2：贝叶斯法则
贝叶斯法则又被称为贝叶斯定理、贝叶斯规则，是指概率统计中的应用所观察到的现象对有关概率分布的主观判断（即先验概率）进行修正(训练过程中不断修正)的标准方法。当分析样本大到接近总体数时，样本中事件发生的概率将接近于总体中事件发生的概率。
贝叶斯统计中的两个基本概念是先验分布和后验分布：
1. 先验分布:
总体分布参数θ的一个概率分布。贝叶斯学派的根本观点，是认为在关于总体分布参数θ的任何统计推断问题中，除了使用样本所提供的信息外，还必须规定一个先验分布，它是在进行统计推断时不可缺少的一个要素。
他们认为先验分布不必有客观的依据，可以部分地或完全地基于主观信念。
2. 后验分布:
根据样本分布和未知参数的先验分布，用概率论中求条件概率分布的方法，求出的在样本已知下，未知参数的条件分布。因为这个分布是在抽样以后才得到的，故称为后验分布。
0x3：贝叶斯估计公式
贝叶斯估计，是在给定训练数据D时，确定假设空间 H 中的最佳假设，一般定义为：
在给定数据 D 以及假设空间 H 中，不同的先验概率下，最可能存在的后验假设分布。
贝叶斯估计的公式如下：
p(h|D) = P(D|H) * P(H) / P(D)
先验概率用 P(h) 表示，它表示了在没有训练数据前假设 h 拥有的初始概率(训练前的一个初始的先验假设)。先验概率反映了我们关于 h 分布的主观认知，如果我们没有这一先验知识，可以简单地将每一候选假设赋予相同的先验概率（平均概率也是一种合理的先验假设）；
P(D)表示训练数据D的先验概率；
P( D | H )表示假设h成立时D的概率；
机器学习中，我们关心的是P( H | D )，即给定D时 H 的成立的概率，称为 H 的后验概率。
贝叶斯公式提供了从先验概率P(h)、P(D)和P( D | H)计算后验概率P(H|D)的方法，即提供了一种从现象回溯规律本质的方法。
对贝叶斯估计的公式，可以这么来理解：
我们的目标P(H|D)，随着P(h)和P(D|H)的增长而增长，随着P(D)的增长而减少。
即如果D独立于H时被观察到的可能性越大，那么D对h的支持度越小，或者说D中包含的对推测出h的有效信息熵越小，即这是一份对我们的推测基本没有帮助的数据。
Relevant Link：
http://www.cnblogs.com/jiangxinyang/p/9378535.html
6. 最大后验估计 MAP - 包含先验假设（正则化）的极大似然估计
0x1：MAP和贝叶斯估计的区别
对于最大后验估计MAP，首先要说明的一点的是，最大后验估计和我们上一章节讨论的贝叶斯估计在数学公式上非常类似，在统计思想上也很类似，都是以最大化后验概率为目的。区别在于：
1. 极大似然估计和极大后验估计MAP只需要返回预估值，贝叶斯估计要计算整个后验概率的概率分布； 2. 极大后验估计在计算后验概率的时候，把分母p(D)给忽略了，在进行贝叶斯估计的时候则不能忽略；
0x2：MAP估计的数学公式
假设 x 为独立同分布的采样，θ为模型参数，f 为我们所使用的模型。那么最大似然估计可以表示为：
现在，假设θ的先验分布为g。通过贝叶斯理论，对于θ的后验分布如下式所示：
后验分布的目标为：
，分母并不影响极大值的求导，因此可以忽略。
最大后验估计可以看做贝叶斯估计的一种特定形式。
0x3：MAP估计举例
假设有五个袋子，各袋中都有无限量的饼干(樱桃口味或柠檬口味)，已知五个袋子中两种口味的比例分别是
樱桃 100%
樱桃 75% + 柠檬 25%
樱桃 50% + 柠檬 50%
樱桃 25% + 柠檬 75%
柠檬 100%
如果只有如上所述条件，那问从同一个袋子中连续拿到2个柠檬饼干，那么这个袋子最有可能是上述五个的哪一个？
我们知道，最大后验概率MAP是正则化的最大似然概率，我们首先采用最大似然估计来解这个问题，写出似然函数。
假设从袋子中能拿出柠檬饼干的概率为p，则似然函数可以写作：
由于p的取值是一个离散值，即上面描述中的0,25%，50%，75%，1。我们只需要评估一下这五个值哪个值使得似然函数最大即可，根据最大似然的计算，肯定得到为袋子5。
上述最大似然估计有一个问题，就是没有考虑到模型本身的概率分布(即没有考虑模型本身的复杂度)(结构化风险)，下面我们扩展这个饼干的问题。对模型自身的复杂度进行先验估计
拿到袋子1的概率是0.1
拿到袋子2的概率是0.2
拿到袋子3的机率是0.4 拿到袋子4的机率是0.2 拿到袋子5的机率是0.1 # 类高斯分布
那同样上述问题的答案呢？这个时候就变MAP了。我们根据公式
写出我们的MAP函数
根据题意的描述可知，p的取值分别为0，25%，50%，75%，1，g的取值分别为0.1，0.2，0.4，0.2，0.1。分别计算出MAP函数的结果为：
0 * 0 * 0.1 = 0
0.25 * 0.25 * 0.2 = 0.0125 0.5 * 0.5 * 0.4 = 0.1 0.75 * 0.75 * 0.2 = 0.1125 1 * 1 * 0.1 = 0.1
由上可知，通过MAP估计可得结果是从第四个袋子中取得的最高。
可以看到，虽然观测结果表明最大似然应该是第5个袋子，但是在加入正则化(模型复杂度)先验后，得到的结果被修正了。
Relevant Link：
https://lagunita.stanford.edu/c4x/Engineering/CS-224N/asset/slp4.pdf https://guangchun.wordpress.com/2011/10/13/ml-bayes-map/ https://en.wikipedia.org/wiki/N-gram http://www.jianshu.com/p/f1d3906e4a3e http://www.cnblogs.com/liliu/archive/2010/11/22/1883702.html http://www.cnblogs.com/xueliangliu/archive/2012/08/02/2962161.html http://www.cnblogs.com/stevenbush/articles/3357803.html http://blog.csdn.net/guohecang/article/details/52313046 http://www.cnblogs.com/burellow/archive/2013/03/19/2969538.html
Copyright (c) 2018 LittleHann All rights reserved