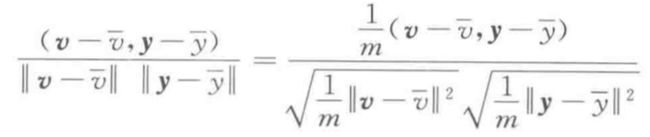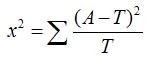1. 为什么要进行特征选择?
0x1:有哪些因素会影响模型利用先验知识?
我们知道,一个算法学习可以成功预测,一个很重要的关键是目标问题隐含了特定模式的先验假设(先验知识),而算法要做的唯一的事情,就是捕获这种先验假设,即通过我们熟悉的模型参数的形式来固话一个生成式或者一个判别式。
从一个具体的虚拟的例子开始说起,但是这个例子和我们再实际工程项目中遇到的所有问题,本质上是一样的。
有一个广告公司,每月会投入一定的广告费,用于提升其销售额,同时,财务部门收集了历史上每个月投入的广告费和销售额的结果:
这是一个非常具体的问题,项目的目标是需要开发一个预测器,帮助决策层判断将来需要投入多少广告费,并且对预期的销售额收入有一个预期判断。
1. 特征数字化编码 - 如何数值化编码是第一个影响最终效果的因素
算法是一个数学的运算和求导得极值过程,要求模型输入的是一个数字化的向量,但是现实生活中的例子不一定都是纯数字化的,当然这个例子本身足够简单,输入和要预测的结果本身已经是数字了,那我们可以直接进行数字化编码,但是在其他领域利于NLP领域,如何进行数字化特征编码就是一个足够引起慎重思考的问题了。
在这个销售预测的例子中,我们将输入样本编码为 1 维向量 X,数值即广告费的数值。预测的结果编码为 1 维的向量 Y,即销售额。
我们用 X 表示广告费,用 Y 表示销售额,这种从现实世界的具体物体,到用数值表示的抽象数值化变换,我们称之为特征函数,简称特征。
如果 X 是向量空间的一个子集,每一个![]() 有时候称为特征向量。
有时候称为特征向量。
如何将现实世界物体编码为输入空间 X 的方式,对理解我们如何利用问题相关的先验知识,是非常重要的。
2. 特征选择 - 对特征进行筛选 and 扭曲变换
在完成特征数字化编码之后,我们可能会遇到一些问题
1)特征数量太多
当然,在本文的销售额预测的例子中没有这个情况,但是我们假设我们引入的特征还有例如当月季节、当月气温、当月流行热点等上千个维度,因为其实这个现象在实际项目中是很常见的,由于物体本身(例如NLP文本)或者我们出于“多多益善”的目的经常会尽可能地将我们认为对最终预测有帮助的特征维度都抽取出来,作为物体的特征向量。
这本身也没有太多问题,但是过多的特征会增大算法运算过程中的CPU和内存需求。
而且很可能还会导致模型欠拟合,这是因为在一些场景下,最终决定结果判断的可能只能其中3-5个核心特征,输入太多的无关特征,可能导致输入了一些“假关联”,这些“假关联”只是恰好在 这批训练样本集中呈现出了某种相关性,但其实其背后并没有隐含任何真实世界的统计规律。
如果模型在训练的过程中,“不小心”错误地引入了这些“假关联”特征,那么可以想象,模型的预测泛化能力是会大打折扣的。
2)在当前特征空间中特征向量线性不可分
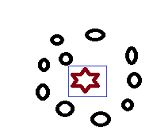
这也是一个很常见的问题,线性可分看起来像是实验课上做demo的场景,在大多数的工程项目中,我们的特征向量都是在当前空间线性不可分的。例如下面这张图:
红星和黑圈无法通过一个线性函数直接进行二分类区分。这个时候其实有两个办法:
1. 选择用非线性分类器进行训练: 例如adaboost、decision tree、dnn这些,但其实本质上,这些模型在训练生成模型的过程中,已经隐含了基于线性分类器组合得到非线性分类器的步骤了。 2. 对原始特征进行扭曲变化,将其转化到另一个高纬度的新特征空间中: 例如基于kernel trick的SVM就是这种情况,通过在原空间样本 X 到希尔伯特空间的特征映射上学习每一个二分类器来实现分类
特征选择,是另一种应用先验知识来处理问题的方法。这是我们本文要重点讨论的一个主题。
3)直接穷举所有特征子集组合可行吗?
在理情况下,我们可以尝试 d 个特征的所有 k 个特征组合,然后选择最优预测结果对应的特征子集。然而,这种穷尽搜索方法通常在计算上是不可行的。
在实际工程中使用的算法中,我们常常采用一些启发式,迭代式的搜索方法来尽可能地获得一个足够好的特征子集。
3. 模型选择
我们知道,虽然有很多可以尝试的共同的特征学习方法,但是“没有免费的午餐”理论指出不存在一种能处理所有问题的极端特征学习期,任何特征学习期都可能在某些问题上失败。
换句话说,每一个特征学习期的成功依赖于数据分布的某种先验假设形式(有时这种先验假设可能不那么明显)。
不同算法的区别在于能否成功捕获这种先验假设,同时也要明白,不同的算法,其拟合能力是不同的,可能对同一份训练数据,会发生欠拟或者过拟。
Relevant Link:
https://www.jianshu.com/p/f485dc676e1c
2. 滤波器特征选择 - 不依赖具体算法模型的feature selection
滤波器方法可能是最简单的特征选择方法,在滤波方法中,我们将某些特征看作独立于其他特征,然后根据一些质量度量标准来估计这些独立特征,然后选择 k 个获得最高评分的特征(此外也可以依据最好的评分确定特征的数量)
0x1:线性相关系数(皮尔森相关系数)- 评价单个特征和预测结果标签的相关性
1. 皮尔森相关系数 - 评价单个特征在一定的评价标准前提下和待预测标签的相关性
一种最直接的方法是依据预测期的错误率来获得特征的评分。
表示 m 个训练样本第 j 个特征值形成的向量,令![]() 表示 m 个样本的目标值。
表示 m 个样本的目标值。
仅仅使用第 j 个特征的经验风险最小化线性预测期的经验平方损失是: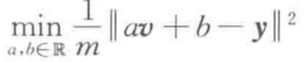
为了求解这个最小化问题,令![]()
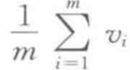 表示特征的平均值,令
表示特征的平均值,令 表示目标的平均值。显然:
表示目标的平均值。显然:
等式右边对 b 求导,令导数等于0,我们得到 b = 0。
将 a,b 的值代入目标函数,我们得到 ,通过选择右式的特征组合,我们的目的是让左式的损失函数值最小。
,通过选择右式的特征组合,我们的目的是让左式的损失函数值最小。
依据最小平方损失对特征排序,等同于依据下面评分的绝对值进行排序(高分表示好的特征):
上面的表达式被称为皮尔森相关系数。分子表示第 j 个特征和目标值方差![]()
![]() 的经验估计,而分母表示第 j 个特征方差
的经验估计,而分母表示第 j 个特征方差![]() 乘上目标值所得方差经验估计的均方根。
乘上目标值所得方差经验估计的均方根。
皮尔森相关系数的取值范围为【-1,1】,这里如果皮尔森相关系数等于 1 或者 -1,表示 v 和 y 之间有线性相关映射关系,且经验风险等于0。
2. 单个特征和待预测标签线性相关性很低,一定意味着这个特征不好吗?
如果皮尔森相关系数等于0,表示 v 到 y 的最优线性映射为各个维度都等于0,这就是说单独只用 v 不足以预测 y。
但是这并不一定意味着 v 是一个坏的特征,比如可能出现这种情况,v 和其他特征组合起来能够很好地预测 y。
假定 x1 是由![]() 上的均匀分布产生,而
上的均匀分布产生,而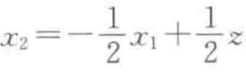 ,这里 z 也是由
,这里 z 也是由![]() 上的均匀分布产生。
上的均匀分布产生。
因此,对于足够大的训练集,第一个特征的皮尔森相关系数可能等于0,因此它可能不被选择,然而,如果不知道第一个特征,没有函数能够很好地预测目标值。
3. Pearson相关系数计算的Scikit-learn版本
Pearson Correlation速度快、易于计算,经常在拿到数据(经过清洗和特征提取之后的)之后第一时间就执行。Scipy的pearsonr方法能够同时计算相关系数和p-value。
#!/usr/bin/python import numpy as np from scipy.stats import pearsonr np.random.seed(0) size = 300 x = np.random.normal(0, 1, size) print "Lower noise", pearsonr(x, x + np.random.normal(0, 1, size)) print "Higher noise", pearsonr(x, x + np.random.normal(0, 10, size))
这个例子中,我们比较了变量在加入噪音之前和之后的差异。
当噪音比较小的时候,p-value接近1,改变后的变量和改变前的变量相关性很强;
当噪音比较大的时候,p-value降低,改变后的变量和改变前的变量相关性降低。
Pearson相关系数的一个明显缺陷是,作为特征排序机制,他只对线性关系敏感。如果关系是非线性的,即便两个变量具有一一对应的关系,Pearson相关性也可能会接近0。
#!/usr/bin/python import numpy as np from scipy.stats import pearsonr x = np.random.uniform(-1, 1, 100000) print pearsonr(x, x**2)[0]
0x2:卡方检验 - 变量之间相关性(这里的变量包括特征或标签值)
卡方检验是一种用途很广的计数资料的假设检验方法。它属于非参数检验的范畴,主要是比较两个及两个以上样本率( 构成比)以及两个分类变量的关联性分析。
其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。
0. 卡方检验概念
卡方检验(chi-square test),也叫作χ2检验。卡方检验有多种方法,最著名的就是皮尔逊卡方检验,也是卡尔·皮尔森提出。我们通常用卡方来检测两个变量or样本的独立性。
卡方检验的理论假设是:一个样本中已发生事件的次数分配会遵守某个特定的理论分配。
通常的讲:观测频数跟实际频数应该没有区别,除非两个变量不是独立的。举个例子:XX公司不同部门职员的性别跟部门两者是独立的么?很明显不是哦。这儿我们的期望男女比例是1.05:1,但是在IT研发部分,比例可能是3:1,在HR、客服等部门,比率可能是1:3了。因此这儿的观测值就跟实际值不一致,我们就可以说两个不是独立的。
1. 通过一个四格卡方检验来阐述卡方检验
下面的表格将实验者分成了2组,随机变量分别为:是否和牛奶、感冒人数。我们现在希望通过卡方检验来揭示这两个变量之间是否具有相关性,即它们之间是否存在依赖推导。
| 感冒人数 | 未感冒人数 | 合计 | 感冒率 | |
| 喝牛奶组 | 43 | 96 | 139 | 30.94% |
| 不喝牛奶组 | 28 | 84 | 112 | 25.00% |
| 合计 | 71 | 180 | 251 | 28.29% |
通过简单的统计我们得出喝牛奶组和不喝牛奶组的感冒率为30.94%和25.00%,两者的差别可能是抽样误差导致,也有可能是牛奶对感冒率真的有影响。
1)建立理论假设统计
为了确定真实原因,我们先假设喝牛奶对感冒发病率是没有影响的,即喝牛奶喝感冒时独立无关的。
所以我们可以得出感冒的发病率实际是(43+28)/(43+28+96+84)= 28.29%
这一步实际上里隐含了条件独立性假设,即将另一个随机变量视为无任何影响,无任何依赖推导,直接计算边缘条件概率。
2)根据理论假设统计重新得到新的概率分布 - 有点类似EM的过程
所以,理论的四格表应该如下表所示:
| 感冒人数 | 未感冒人数 | 合计 | |
| 喝牛奶组 | 139*0.2829 = 39.3231 | 139*(1-0.2829) = 99.6769 | 139 |
| 不喝牛奶组 | 112*0.2829 = 31.6848 | 112*(1-0.2829) = 80.3152 | 112 |
| 合计 | 71 | 180 | 251 |
如果喝牛奶喝感冒真的是独立无关的,那么四格表里的理论值和实际值差别应该会很小。
3)计算理论值和实际值之间的差距
x2用于衡量实际值与理论值的差异程度(也就是卡方检验的核心思想),包含了以下两个信息:
1. 实际值与理论值偏差的绝对大小(由于平方的存在,差异是被放大的) 2. 差异程度与理论值的相对大小
上面牛奶的的例子我们计算得:
卡方 = (43 - 39.3231)平方 / 39.3231 + (28 - 31.6848)平方 / 31.6848 + (96 - 99.6769)平方 / 99.6769 + (84 - 80.3152)平方 / 80.3152 = 1.077
4)卡方分布的临界值
上一步我们得到了卡方的值 = 1.077,但是这个值意味着什么呢?如何通过卡方的值来判断喝牛奶和感冒是否真的是独立无关的?也就是说,怎么知道无关性假设是否可靠?
基本上来说:
卡方值越大,假设成立的概率就越小,即随机变量间相关性越大;
卡方值越小,假设成立的概率就越大,即随机变量间相关性越小。
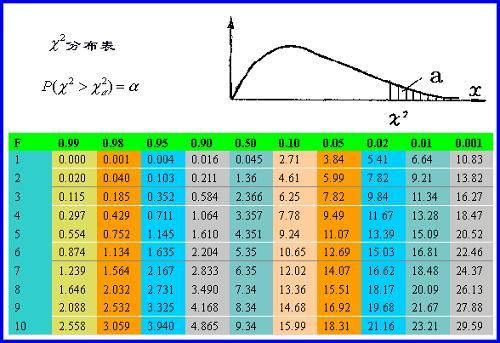
下面是卡方分布的临界值表。
表格里的值代表着:如果卡方值大于对应的阈值,则至少有对应的概率,我们的假设是成立的。
而具体应该查表格的哪一行,这里需要用到一个自由度的概念,自由度等于:F = (行数 - 1) * (列数 - 1)。对这个例子来说,自由度F = 1 * 1 = 1。
在牛奶的这个例子中,对应的是F = 1,即我们需要查第一行。
我们计算得到的卡方检验值为 1.077,介于P(0.1)和P(0.5)这两栏之间,所以我们可以说:
喝牛奶和感冒之间有至少50%的概率,是独立不相关的;
但是1.077超过了和P(0.9)和和P(0.95)的阈值,所以,“喝牛奶和感冒之间独立性假设有95%的概率成立”这句话是错了(有点绕,理解一下)。
所以,综上,所以喝牛奶和感冒独立不相关的假设不成立。
Relevant Link:
https://blog.csdn.net/snowdroptulip/article/details/78770088 https://blog.csdn.net/gdanskamir/article/details/54913233
0x3:互信息估计
以上就是经典的互信息公式了。想把互信息直接用于特征选择其实不是太方便:
1. 它不属于度量方式,也没有办法归一化,在不同数据及上的结果无法做比较; 2. 对于连续变量的计算不是很方便(X和Y都是集合,x,y都是离散的取值),通常变量需要先离散化,而互信息的结果对离散化的方式很敏感。
最大信息系数克服了这两个问题。它首先寻找一种最优的离散化方式,然后把互信息取值转换成一种度量方式,取值区间在[0,1]。minepy提供了MIC功能。
反过头来看y=x^2这个例子,MIC算出来的互信息值为1(最大的取值)。
#!/usr/bin/python import numpy as np from minepy import MINE m = MINE() x = np.random.uniform(-1, 1, 10000) m.compute_score(x, x**2) print m.mic()
0x4:接受操作特征(ROC)曲线的面积
总体来说,滤波评分方法的思想是:在一定的评价标准(损失函数)下,评估特征对最终预测标签结果准确性的贡献度。
Relevant Link:
https://blog.csdn.net/gdanskamir/article/details/54913233 https://www.cnblogs.com/hhh5460/p/5186226.html
3. 贪婪特征选择方法 - 需要依赖具体算法模型得到评价分值
贪婪选择是另一个比较常用的特征选择方法。和滤波方法不同,贪婪选择方法伴随着学习算法的过程,迭代地进行。
0x1:前向贪婪选择方法
最简单的贪婪选择的例子是前向贪婪选择方法。
我们从一个空集开始,然后逐步每次添加一个特征到选择的特征集。
给定当前选择的特征集![]() ,我们遍历所有的
,我们遍历所有的![]() ,然后在
,然后在![]() 特征集上应用学习算法。每一个候选特征选择都取得一个不同的预测器,我们选择添加特征使得预测器的风险最小(经验最小化原则)。对应这个最小风险的候选特征就是本轮选择的特征。
特征集上应用学习算法。每一个候选特征选择都取得一个不同的预测器,我们选择添加特征使得预测器的风险最小(经验最小化原则)。对应这个最小风险的候选特征就是本轮选择的特征。
持续喝个过程知道我们选择了 k 个特征,这里 k 表示预先定义的可以承担的特征数,或者得到一个足够精度的预测器。
0x2:反向终止算法
和前向贪婪选择方法相对的是,反向终止算法。我们从全部特征组合的集合开始,然后逐步从特征集合中一次减少一个特征。
给定我们当前选择的特征集![]() 。每个这样的做法取得一个不同的预测期,然后我们选择去掉特征 i 是的预测期从特征集
。每个这样的做法取得一个不同的预测期,然后我们选择去掉特征 i 是的预测期从特征集![]() 得到最小的风险(在训练集或者验证集上)
得到最小的风险(在训练集或者验证集上)
0x3:基于有监督学习模型的特征排序 (Model based ranking)
这种方法的思路是直接使用你要用的有监督机器学习算法,针对每个单独的特征和响应变量(标签值y)建立预测模型。
其实Pearson相关系数等价于线性回归里的标准化回归系数。
假如某个特征和响应变量之间的关系是非线性的,可以用基于树的方法(决策树、随机森林)、或者扩展的线性模型等。基于树的方法比较易于使用,因为他们对非线性关系的建模比较好,并且不需要太多的调试。但要注意过拟合问题,因此树的深度最好不要太大,再就是运用交叉验证。
我们在著名的波士顿房价数据集上使用sklearn的随机森林回归给出一个单变量选择的例子:
#!/usr/bin/python import numpy as np from sklearn.cross_validation import cross_val_score, ShuffleSplit from sklearn.datasets import load_boston from sklearn.ensemble import RandomForestRegressor #Load boston housing dataset as an example boston = load_boston() X = boston["data"] Y = boston["target"] names = boston["feature_names"] rf = RandomForestRegressor(n_estimators=20, max_depth=4) scores = [] for i in range(X.shape[1]): score = cross_val_score(rf, X[:, i:i+1], Y, scoring="r2", cv=ShuffleSplit(len(X), 3, .3)) scores.append((round(np.mean(score), 3), names[i])) res = sorted(scores, reverse=True) for i in res: print i
0x3:稀疏诱导范数
4. 特征操作与归一化
特征操作或归一化包括在每一个源特征上的简单变换。这些变换可能使得我们假设类的近似误差或估计误差更低或者能够得到一个更快的算法。
与特征选择的问题类似,特征操作与归一化充满了“玄学”,它需要我们具体问题具体分析,这里没有绝对好或绝对坏的变换,而是每一个特征变换与在这些特征矢量上的学习算法,以及这个问题相关的先验假设密切相关。
0x1:常用的特征变换
接下来,我们用![]() 表示在 m 个训练样本上的特征 f,同样,我们用
表示在 m 个训练样本上的特征 f,同样,我们用 表示所有样本特征的经验均值。
表示所有样本特征的经验均值。
1. 中心化
2. 归一化范围
当然,很容易将范围变换为【0,b】或【-b,b】
3. 标准化
这个变换使得所有特征有 0 均值和 1 方差。形式上,令 表示特征的经验方差,那么设置
表示特征的经验方差,那么设置
4. 裁剪变换
这个变换裁剪特征的高值或低值
5. sigmoidal变换
这个变换在特征上用到了sigmoid函数,例如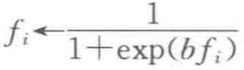 ,这里 b 是用户自定义参数。这个变换可以认为是一种软版本的裁剪变换。它对接近于 0 的值值有一些作用,并且与远离 0 的裁剪变换很相似。
,这里 b 是用户自定义参数。这个变换可以认为是一种软版本的裁剪变换。它对接近于 0 的值值有一些作用,并且与远离 0 的裁剪变换很相似。
6. 对数变换
这个变换是![]() ,这里 b 是用户自定义参数。这个变换广泛地用于当特征是计数型特征的情况下。例如,假定特征表示在一个文档中某个词出现的次数。那么,某个词出现一次与没有出现的区别,要比一个词出现1000次还是1001次更为重要。
,这里 b 是用户自定义参数。这个变换广泛地用于当特征是计数型特征的情况下。例如,假定特征表示在一个文档中某个词出现的次数。那么,某个词出现一次与没有出现的区别,要比一个词出现1000次还是1001次更为重要。
简单来说,对数变换对值较小时的变化更敏感,值越大,敏感度越低。从本质上看,和标准化和归一化的思想很类似。
Relevant Link:
https://www.cnblogs.com/hhh5460/p/5186226.html