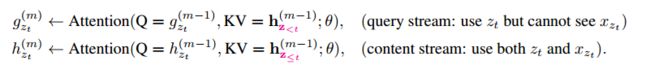从语言模型到XLNet的知识点笔记
文章目录
- 前言
- 一、LM
- 二、RNN vs LSTM
- (一)RNN
- (二)LSTM
- (三)GRU
- (四)RNN网络的基本应用
- 三、Attention Mechanism
- 四、Transformer
- 五、TransformerXL
- 六、Pretrain + Finetune Pipeline
- (一)ELMo
- (二)GPT
- (三)BERT
- (四)GPT2.0
- (五)XLNet
- 总结
- 作者简介
- 参考文献
前言
前段时间一直在忙产品上线的事情,对于NLP领域的新宠“Pretrain+Finetune”范式以及BERT、XLNet等模型都是零零散散的了解,很多细节一知半解,趁着这几天有些时间,索性把相关的paper都从头看一遍,加深理解。大规模Pretrain加小规模Finetune其实并不是最近才有的Pipeline,几年前在CV领域已被提出并证实其在Transfer方面的效果。但CV领域的Pretrain是基于大规模的监督数据,而在NLP领域,标注数据是非常稀缺的,因此才一直不愠不火。直到BERT的推出,基于非监督语言模型的Pretrain才逐渐火爆(毕竟无监督的语料数据太容易获得了),因此笔者就从LM开始,把最近一些前沿的重点工作做下简单的总结,也算是做下笔记加深印象。
一、LM
语言模型(Language Model,LM)是一个非常基础的概念,在自然语言处理的各项任务中起到极其重要的作用。同时对于后续知识点的掌握是一个不可或缺的储备,因而文章的开头还是先简单熟悉一下LM。
1、定义:对于长度为 n n n 的语言序列 w 1 , w 2 , . . . , w n w_1,w_2,...,w_n w1,w2,...,wn,其语言模型指的就是该语言序列的共现概率,也就是联合概率分布 p ( w 1 , w 2 , . . . , w n ) p(w_1,w_2,...,w_n) p(w1,w2,...,wn)。
2、概率计算:根据贝叶斯链式法则,语言模型的联合概率分布可以拆解为: p ( w 1 , w 2 , . . . , w n ) = p ( w 1 ) ∗ p ( w 2 ∣ w 1 ) ∗ p ( w 3 ∣ w 1 , w 2 ) . . . p ( w n ∣ w 1 , w 2 , . . . , w n − 1 ) p(w_1,w_2,...,w_n)=p(w_1)*p(w_2|w_1)*p(w_3|w_1,w_2)...p(w_n|w_1,w_2,...,w_{n-1}) p(w1,w2,...,wn)=p(w1)∗p(w2∣w1)∗p(w3∣w1,w2)...p(wn∣w1,w2,...,wn−1) 其模型参数 p ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) p(w_i|w_1,w_2,...,w_{i-1}) p(wi∣w1,w2,...,wi−1) 通过极大似然估计可得: p ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) = c o u n t ( w 1 , w 2 , . . . , w i − 1 , w i ) ∑ w c o u n t ( w 1 , w 2 , . . . , w i − 1 , w ) p(w_i|w_1,w_2,...,w_{i-1})=\frac{count(w_1,w_2,...,w_{i-1},w_i)}{\sum_w count(w_1,w_2,...,w_{i-1},w)} p(wi∣w1,w2,...,wi−1)=∑wcount(w1,w2,...,wi−1,w)count(w1,w2,...,wi−1,wi) 上述的参数计算方式有两个明显的缺点:
-
计算量大:假设训练语料中字典大小为 V V V,语言序列长度最长为 n n n,语言序列中的 w i w_i wi 都来自字典,那么模型参数量级为 V n V^n Vn,也就是意味着模型参数量会随着语言序列长度的增长而指数级暴增。
-
数据稀疏:由于整个模型的参数量级为 V n V^n Vn,根据似然估计的计算方式,一般的训练语料中,会出现大量的参数为0的情况(一般的训练语料很难覆盖到所有的 w 1 , w 2 , . . . , w n w_1,w_2,...,w_n w1,w2,...,wn)。
3、N-gram模型:为了解决上述参数量大而带来的计算问题,引入了马尔科夫假设,也就是任意一个当前词 w i w_i wi 出现的概率,只跟其上文的前 N − 1 N-1 N−1 个词有关,这样的模型就称为N-gram模型。一般 N N N 的取值为1、2、3,分别对应unigram、bigram、trigram模型;以bigram为例,其概率模型可以表示为: p ( w 1 , w 2 , . . . , w n ) = ∏ i = 1 n p ( w i ∣ w i − 1 ) p(w_1,w_2,...,w_n)=\prod_{i=1}^n{p(w_i|w_{i-1})} p(w1,w2,...,wn)=i=1∏np(wi∣wi−1) 当 i = 1 i=1 i=1 时, w 0 w_0 w0 一般用 < S > <S> <S> 表示,代表起始符。通过上述概率模型的表述,可以看出模型的参数量级从 V n V^n Vn 降为 V 2 V^2 V2。但是N-gram模型依然会面临OOV问题,也就是测试集存在训练集未出现的词。为了解决OOV问题,还需要在N-gram模型中引入平滑技术,以最常见的加法平滑为例,其模型参数可以表示为: P ( w i ∣ w i − 1 ) = c o u n t ( w i − 1 , w i ) + λ ∑ w c o u n t ( w i − 1 , w ) + λ ∣ V ∣ P(w_i|w_{i-1})=\frac{ count(w_{i-1},w_i) + \lambda}{\sum_wcount(w_{i-1},w) + \lambda\vert V \vert} P(wi∣wi−1)=∑wcount(wi−1,w)+λ∣V∣count(wi−1,wi)+λ 其中 λ \lambda λ 表示平滑因子, ∣ V ∣ \vert V \vert ∣V∣ 表示字典大小,这样子就可以保证模型参数不为0。
4、基于神经网络的语言模型(Neural Network Language Model,NNLM):上述的N-gram本质上是基于统计频次的模型,缺乏泛化能力。而基于神经网络的语言模型赋予每个词向量化的能力,丰富其表征能力,从而提高模型泛化的能力以及避免OOV带来的影响。如图1所示就是基于前向神经网络的语言模型。
5、语言模型的评价指标:perplexity(困惑度)
-
在信息论中,一般采用相对熵来衡量两个分布之间的相似度。对于随机变量 X X X,其熵、交叉熵以及相对熵的定义如下:
H ( p ) = − ∑ i p ( x i ) l o g p ( x i ) H(p)=-\sum_i{p(x_i)logp(x_i)} H(p)=−i∑p(xi)logp(xi) H ( p , q ) = − ∑ i p ( x i ) l o g q ( x i ) H(p,q)=-\sum_i{p(x_i)logq(x_i)} H(p,q)=−i∑p(xi)logq(xi) D ( p ∣ ∣ q ) = H ( p , q ) − H ( p ) = ∑ i p ( x i ) l o g p ( x i ) / q ( x i ) D(p||q)=H(p,q)-H(p)=\sum_i{p(x_i)logp(x_i)/q(x_i)} D(p∣∣q)=H(p,q)−H(p)=i∑p(xi)logp(xi)/q(xi)其中 p p p 是样本的真实分布, q q q 是模型的预测分布。 -
对于语言模型而言,计算相对熵评测其模型效果时, H ( p ) H(p) H(p) 是一个固定不变的值(真实分布唯一),因此可以用 H ( p , q ) H(p,q) H(p,q) 来衡量两个分布之间的相似度。对于样本的真实分布可以表示为:
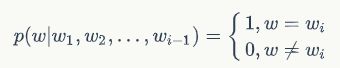
模型的预测分布可以表示为 q ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) q(w_i|w_1,w_2,...,w_{i-1}) q(wi∣w1,w2,...,wi−1),因此,对于语言序列 w 1 , w 2 , . . . , w n w_1,w_2,...,w_n w1,w2,...,wn,语言模型得到的交叉熵可以表示为: H ( p , q ) = − ∑ w p ( w ) l o g q ( w ) = − 1 n ∑ i = 1 n ( ∑ w p ( w ∣ w 1 , w 2 , . . . , w i − 1 ) l o g q ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) ) = − 1 n ∑ i = 1 n ( 1 ∗ l o g q ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) + ∑ w ≠ w i 0 ∗ l o g q ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) ) = − 1 n ∑ i = 1 n l o g q ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) = − 1 n l o g ∏ i = 1 n q ( w i ∣ w 1 , w 2 , . . . , w i − 1 ) = − 1 n l o g q ( w 1 , w 2 , . . . , w n ) H(p,q)=-\sum_w{p(w)logq(w)}\\=-\frac{1}{n}\sum_{i=1}^n(\sum_wp(w|w_1,w_2,...,w_{i-1})logq(w_i|w_1,w_2,...,w_{i-1}))\\=-\frac{1}{n}\sum_{i=1}^n(1*logq(w_i|w_1,w_2,...,w_{i-1})+\sum_{w\neq w_i}0*logq(w_i|w_1,w_2,...,w_{i-1}))\\=-\frac{1}{n}\sum_{i=1}^nlogq(w_i|w_1,w_2,...,w_{i-1})\\=-\frac{1}{n}log\prod_{i=1}^nq(w_i|w_1,w_2,...,w_{i-1})\\=-\frac{1}{n}logq(w_1,w_2,...,w_n) H(p,q)=−w∑p(w)logq(w)=−n1i=1∑n(w∑p(w∣w1,w2,...,wi−1)logq(wi∣w1,w2,...,wi−1))=−n1i=1∑n(1∗logq(wi∣w1,w2,...,wi−1)+w̸=wi∑0∗logq(wi∣w1,w2,...,wi−1))=−n1i=1∑nlogq(wi∣w1,w2,...,wi−1)=−n1logi=1∏nq(wi∣w1,w2,...,wi−1)=−n1logq(w1,w2,...,wn)perplexity的定义: p e r p l e x i t y = 2 H ( p , q ) = ( q ( w 1 , w 2 , . . . , w n ) ) − 1 / n = 1 q ( w 1 , w 2 , . . . , w n ) n perplexity=2^{H(p,q)}=(q(w_1,w_2,...,w_n))^{-1/n}=\sqrt[n]{\frac{1}{q(w_1,w_2,...,w_n)}} perplexity=2H(p,q)=(q(w1,w2,...,wn))−1/n=nq(w1,w2,...,wn)1 对于语料库中的语言序列 w 1 , w 2 , . . . , w n w_1,w_2,...,w_n w1,w2,...,wn 来说,其perplexity越小代表通过语言模型计算得到这个序列的概率越高,也代表语言模型对语料库的拟合越好。
二、RNN vs LSTM
(一)RNN
1、自然语言处理本质上属于序列问题,循环神经网络(Recurrent Neural Network,RNN)就是为了解决序列问题而被提出的。相比传统的DNN或者CNN网络,它的优势在于:
-
可以更加便捷地学习到足够长的上文信息;在语言模型的学习过程中,N-gram模型随着 N N N 的变大会带来模型参数量级的指数增长,而RNN可以很好地解决这个问题,理论上可以获得上文所有序列的信息。
-
可以适应序列数据不定长输入的特点;在自然语言处理的任务中,输入的序列通常都是不定长的,而传统的DNN跟CNN输入输出都是固定维度的。
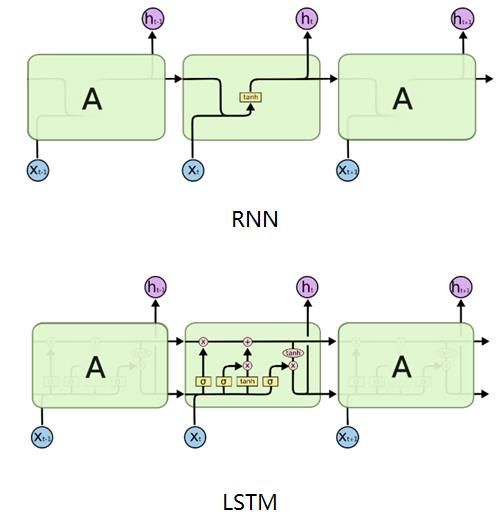
2、定义:给定一个长度为 t t t 的输入样本 x 0 , x 1 , x 2 , . . . , x t x_0,x_1,x_2,...,x_t x0,x1,x2,...,xt,其在 t t t 时刻对应的模型输入是 x t x_t xt(注意: x t x_t xt 是一个向量),该时刻的隐层状态 h t h_t ht 是由当前时刻模型的输入 x t x_t xt 跟上一时刻模型的隐层状态 h t − 1 h_{t-1} ht−1 所决定的。对于每个时刻的模型输出 O t O_t Ot 则由当前时刻的隐藏状态 h t h_t ht 所决定。具体如图2所示。其中 A A A 代表单个时刻的网络模型,每个时刻的网络模型参数是共享的。从图中可以看出,对于不定长的输入,RNN可以通过横向扩展网络结构来训练,而由于横向的网络模型参数是共享的,所以这种结构天然适合不定长的序列任务,也是RNN的核心思想。
3、RNN的前向传播
对于 t t t 时刻,假设输入为 x t x_t xt,那么隐层状态为: h t = ϕ ( U x t + W h t − 1 + b ) h_t=\phi(Ux_t +Wh_{t-1} + b) ht=ϕ(Uxt+Wht−1+b) 其中 U U U 为输入到隐层的权重参数矩阵, W W W 为相邻时刻隐层间的权重参数矩阵(也叫自循环参数矩阵), b b b 是偏置参数, ϕ \phi ϕ 是激活函数。最终模型的输出就是: O t = σ ( V h t + c ) O_t=\sigma(Vh_t+c) Ot=σ(Vht+c) 其中 V V V 是隐层到输出层的权重参数矩阵, c c c 是偏置参数, σ \sigma σ 是激活函数。以上列举的模型参数 U , W , V , b , c U,W,V,b,c U,W,V,b,c 是所有时刻共享的。
4、RNN的反向传播
RNN的损失函数一般采用交叉熵,对于时刻 t t t,交叉熵定义如下: L t = − 1 m ∑ i = 1 m y t i l o g ( O t i ) L_t=-\frac{1}{m}\sum_{i=1}^my_t^ilog(O_t^i) Lt=−m1i=1∑mytilog(Oti) 其中 m m m 表示样本的数量, y t i y_t^i yti 表示第 i i i 个样本第 t t t 时刻的真实输出, O t i O_t^i Oti 表示第 i i i 个样本第 t t t 时刻的实际输出,因此总的损失函数如下: L = ∑ t L t L=\sum_tL_t L=t∑Lt 定义了损失函数,就可以通过梯度下降法来训练RNN模型。梯度的计算采用的是BPTT(Back Propagation Through Time)。对于 V V V 的梯度,计算比较简单: ∂ L t ∂ V = ∂ L t ∂ O t ∂ O t ∂ V \frac{\partial{L_t}}{\partial{V}}=\frac{\partial{L_t}}{\partial{O_t}}\frac{\partial{O_t}}{\partial{V}} ∂V∂Lt=∂Ot∂Lt∂V∂Ot 而对于 U , W U,W U,W 的梯度,相对比较复杂,需要沿着时间轴反向传播: ∂ L t ∂ U = ∑ i = 1 t ∂ L t ∂ O t ∂ O t ∂ h t ( ∏ j = i + 1 t ∂ h j ∂ h j − 1 ) ∂ h i ∂ U \frac{\partial{L_t}}{\partial{U}}=\sum_{i=1}^t\frac{\partial{L_t}}{\partial{O_t}}\frac{\partial{O_t}}{\partial{h_t}}(\prod_{j=i+1}^t\frac{\partial{h_j}}{\partial{h_{j-1}}})\frac{\partial{h_i}}{\partial{U}} ∂U∂Lt=i=1∑t∂Ot∂Lt∂ht∂Ot(j=i+1∏t∂hj−1∂hj)∂U∂hi ∂ L t ∂ W = ∑ i = 1 t ∂ L t ∂ O t ∂ O t ∂ h t ( ∏ j = i + 1 t ∂ h j ∂ h j − 1 ) ∂ h i ∂ W \frac{\partial{L_t}}{\partial{W}}=\sum_{i=1}^t\frac{\partial{L_t}}{\partial{O_t}}\frac{\partial{O_t}}{\partial{h_t}}(\prod_{j=i+1}^t\frac{\partial{h_j}}{\partial{h_{j-1}}})\frac{\partial{h_i}}{\partial{W}} ∂W∂Lt=i=1∑t∂Ot∂Lt∂ht∂Ot(j=i+1∏t∂hj−1∂hj)∂W∂hi 通过上述梯度的公式可以看出,随着序列长度的扩展,梯度会由于小数的累乘而变得接近于0,那么就会出现梯度弥散问题,因此RNN一般也就适用于序列长度比较短的场景。为了克服RNN在长依赖上的缺点,LSTM模型被提出。
(二)LSTM
1、定义:LSTM即Long Short Memory Network,是为了克服RNN在长期依赖问题上的缺陷而被提出,属于RNN的一种变种,通过一堆门控单元来对历史信息进行选择性地传递或者遗忘,从而有效地捕捉上文信息。
2、LSTM的前向传播
- 单元状态流
单元状态流可以理解为LSTM的记忆流水线,上面存储着LSTM对上文信息的提取记忆。主要是通过遗忘门、输入门以及输出门来管控。
- 遗忘门
如图所示, h t − 1 h_{t-1} ht−1 表示上一个时刻的隐层状态, x t x_t xt 表示 t t t 时刻的输入(注意: x t x_t xt 是一个向量), W f W_f Wf 表示遗忘门权重参数(该权重参数可以拆分为两个权重参数矩阵,分别对应输入状态跟上一个时刻隐层状态), b f b_f bf 表示遗忘门偏置参数, σ \sigma σ 表示sigmoid激活函数,这样子可以确保遗忘门输出 f t f_t ft 是一个0到1之间的数值,这个数值决定有多少历史信息需要遗忘。1表示完全保留,0表示完全舍弃。
- 输入门
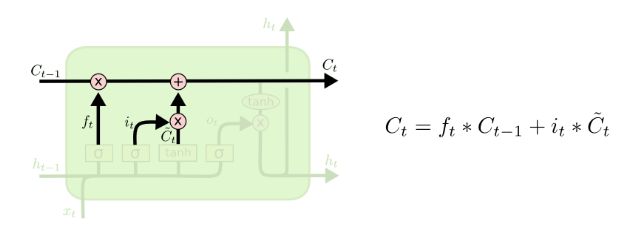
如图所示, W i W_i Wi 表示输入门权重参数, b i b_i bi 表示输入门偏置参数, σ \sigma σ 表示sigmoid激活函数,这样子可以确保输入门输出 i t i_t it 是一个0到1之间的数值,这个数值决定有多少输入信息需要记忆。1表示完全保留,0表示完全舍弃。 W C W_C WC 表示权重参数, b C b_C bC 表示偏置参数, tanh \tanh tanh 表示激活函数,输出值 C t ~ \tilde{C_t} Ct~ 表示当前时刻流向单元状态的值。输入门控制的就是有多少 C t ~ \tilde{C_t} Ct~ 流入单元状态。
根据图7可以看出,最终单元状态保存的信息就是通过对上一个时刻的状态信息 C t − 1 C_{t-1} Ct−1 进行选择性遗忘,对当前时刻的输入单元状态信息 C t ~ \tilde{C_t} Ct~ 进行选择性保留,从而组成当前时刻的最终的单元状态信息 C t C_t Ct。
- 输出门
如图所示, W O W_O WO 表示输出门权重参数, b O b_O bO 表示输出门偏置参数, σ \sigma σ 表示sigmoid激活函数,这样子可以确保输出门输出 O t O_t Ot 是一个0到1之间的数值,这个数值决定有多少输出信息需要记忆。1表示完全保留,0表示完全舍弃。
(三)GRU
GRU(Gated Recurrent Unit)是LSTM的变种,LSTM具有3个门(输入门、输出门、遗忘门),而GRU只有2个门(更新门、重置门),并且GRU也抛弃了单元状态的概念,由于GRU的模型参数变少,所以训练时候更好收敛。
如图所示, r t r_t rt 表示重置门, z t z_t zt 表示更新门。
(四)RNN网络的基本应用
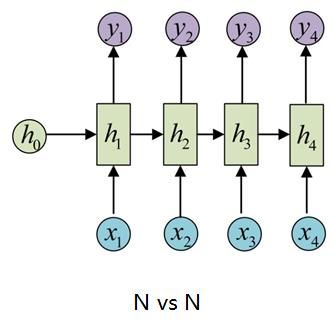
1、N vs N
如图所示,输入输出等长。典型的应用场景有:序列标注、语言建模(输入一般是 S , w 1 , w 2 , . . . , w n S,w_1,w_2,...,w_n S,w1,w2,...,wn,输出则是 w 1 , w 2 , . . . , w n , E w_1,w_2,...,w_n,E w1,w2,...,wn,E,这就是典型的char RNN)等。
2、N vs 1
如图所示,输入是一个序列,输出则是单个时刻的向量,后面再接个softmax分类器。典型的应用场景有:文本分类、情感分析等。
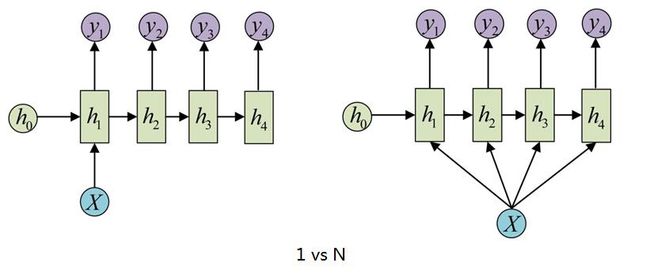
3、1 vs N
如图所示,输入是单个时刻的向量,输出则是一个序列。典型的应用场景有:图像生成文字等。
4、N vs M
如图所示,输入输出可以是不等长序列,该模型先是将输入序列编码成一个上下文向量,然后根据上下文向量解码成一个不等长的输出序列,因此该结构也叫encoder-decoder结构,也叫seq2seq模型。典型的应用场景有:
机器翻译、文本摘要、语音识别、阅读理解(输入是文章内容以及问题,输出是问题对应的回答)。
三、Attention Mechanism
上文已经介绍了seq2seq的模型结构,该网络结构在处理序列到序列的任务中应用非常广泛。但其存在2个明显不足的问题:
-
encoder将所有的输入序列信息压缩到固定维度的上下文向量 C C C中,很显然是存在信息的有损压缩的,尤其是当输入序列长度过长的情况下。
-
decoder在解码的时候,每一个时刻的上下文向量 C C C是固定不变的,但在实际情况中,decoder端某个时刻往往只对应encoder端的某几个时刻的序列值,而不是所有时刻。举个例子,在机器翻译中,对于样本对“我爱中国——I Love China”,输出序列的“China”其实只跟输入序列的“中国”有关。
因此,为了解决上述存在的问题,Attention Mechanism(AM)被提出。
1、Attention机制
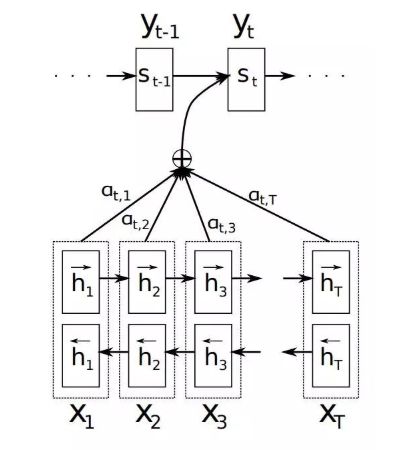
如图所示,对于decoder,定义条件概率如下: p ( y t ∣ y 1 , y 2 , . . . , y t − 1 , X ) = g ( y t − 1 , s t , c t ) p(y_t|y_1,y_2,...,y_{t-1},X) = g(y_{t-1},s_t,c_t) p(yt∣y1,y2,...,yt−1,X)=g(yt−1,st,ct) 其中 s t s_t st 表示decoder在 t t t 时刻的隐层状态, c t c_t ct 表示decoder在 t t t 时刻的上下文向量。对于 s t s_t st 可以表示如下: s t = f ( s t − 1 , y t − 1 , c t ) s_t = f(s_{t-1},y_{t-1},c_t) st=f(st−1,yt−1,ct) 其中 c t c_t ct 表示如下: c t = ∑ k = 1 T α t k h k c_t= \sum_{k=1}^T\alpha_{tk}h_k ct=k=1∑Tαtkhk 其中 t t t 表示decoder第 t t t 个时刻, h k h_k hk 表示encoder的第 k k k 个时刻的隐层状态, α t k \alpha_{tk} αtk 表示decoder的第 t t t 个时刻跟encoder的第 k k k 个时刻的权值,可以理解为是源端第 k k k 个词对目标端第 t t t 个词的影响程度, α t k \alpha_{tk} αtk 的计算如下: α t k = e x p ( e t k ) ∑ k = 1 T e x p ( e t k ) \alpha_{tk}=\frac{exp(e_{tk})}{\sum_{k=1}^Texp(e_{tk})} αtk=∑k=1Texp(etk)exp(etk) e t k = s c o r e ( s t − 1 , h k ) e_{tk}=score(s_{t-1},h_k) etk=score(st−1,hk) e t k e_{tk} etk 是一个对齐模型,用于衡量encoder端第 k k k 个位置的词,对于decoder端第 t t t 个位置的词的对齐程度(影响程度)。对齐模型 e t k e_{tk} etk 最常见的就是点乘 s c o r e ( s t − 1 , h k ) = s t − 1 T h k score(s_{t-1},h_k) = s_{t-1}^Th_k score(st−1,hk)=st−1Thk。
2、Self-Attention
传统的Attention机制是根据encoder端跟decoder端的隐层状态来计算Attention Score的,得到的结果是源端跟目标端之间词与词的依赖关系。但Self-Attention是分别在encoder跟decoder端计算Attention Score的,先是在encoder端计算Attention Score捕捉源端自身词与词之间的依赖关系,然后将encoder端得到的Attention Score加入到decoder端,捕捉目标端自身词与词之间的依赖关系以及目标端跟源端词与词之间的依赖关系。相对比传统的Attention机制,Self-Attention的优势在于不仅可以捕捉目标端跟源端之间词与词的依赖关系,还可以捕捉源端或者目标端自身词与词的依赖关系。
3、Scaled Dot-Product Attention
之所以提Scaled Dot-Product Attention是因为一般Self-Attention都是结合Scaled Dot-Product Attention实现的。假设输入为 X = x 1 , x 2 , . . . , x m X={x_1,x_2,...,x_m} X=x1,x2,...,xm,其中 x m x_m xm 是维度为 d m o d e l d_{model} dmodel 的向量。首先将输入 X X X 经过线性变化得到 Q , K , V Q,K,V Q,K,V(Self-Attention的体现),分别表示Query、Key、Value。如图所示, Q , K Q,K Q,K 做一个矩阵相乘的操作,得到输入端自身词与词之间的依赖关系,然后依次经过尺寸变换(防止输入维度过大导致梯度落在softmax函数的边缘区域,从而训练难收敛)、掩码(可选操作,主要用于对时间先后关系的表示)、SoftMax操作,得到最终的Self-Attention矩阵。将Self-Attention矩阵跟 V V V做矩阵相乘,就可以得到最后的输出结果。 A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dkQKT)V Q = X W Q Q = X W^Q Q=XWQ K = X W K K = X W^K K=XWK V = X W V V = X W^V V=XWV 其中 X ∈ R m × d m o d e l X\in{R^{m \times d_{model}}} X∈Rm×dmodel, W Q ∈ R d m o d e l × d m o d e l W^Q\in{R^{d_{model} \times d_{model}}} WQ∈Rdmodel×dmodel, W K ∈ R d m o d e l × d m o d e l W^K\in{R^{d_{model} \times d_{model}}} WK∈Rdmodel×dmodel, W V ∈ R d m o d e l × d m o d e l W^V\in{R^{d_{model} \times d_{model}}} WV∈Rdmodel×dmodel, d k = d m o d e l d_k=d_{model} dk=dmodel 表示 Q , K Q,K Q,K 的向量维度。
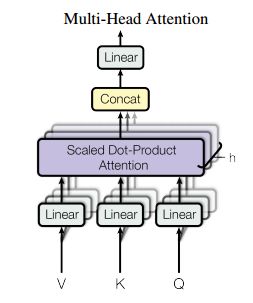
4、Multi-Head Attention
上述的Attention都是只有一套 Q , K , V Q,K,V Q,K,V,而Multi-Head Attention是在一套 Q , K , V Q,K,V Q,K,V 的基础上线性变化得到 h h h 套 Q i , K i , V i Q_i,K_i,V_i Qi,Ki,Vi,分别得到输出矩阵之后再进行拼接。之所以采用多套 Q i , K i , V i Q_i,K_i,V_i Qi,Ki,Vi 一方面是可以加速Attention的计算,一方面是可以获取不同空间维度的依赖信息。个人理解这应该是一个工程上的trick。 M u l t i H e a d ( Q , K , V ) = C o n c a t ( h e a d 1 , . . . , h e a d h ) W O MultiHead(Q,K,V)=Concat(head_1,...,head_h)W^O MultiHead(Q,K,V)=Concat(head1,...,headh)WO 其中 h e a d i = A t t e n t i o n ( Q W i Q , K W i K , V W i V ) head_i=Attention(QW_i^Q,KW_i^K,VW_i^V) headi=Attention(QWiQ,KWiK,VWiV) 其中 W i Q ∈ R d m o d e l × d k W_i^Q\in{R^{d_{model} \times d_k}} WiQ∈Rdmodel×dk, W i K ∈ R d m o d e l × d k W_i^K\in{R^{d_{model} \times d_k}} WiK∈Rdmodel×dk, W i V ∈ R d m o d e l × d v W_i^V\in{R^{d_{model} \times d_v}} WiV∈Rdmodel×dv, W i O ∈ R h d v × d m o d e l W_i^O\in{R^{hd_v \times d_{model}}} WiO∈Rhdv×dmodel。假设 d m o d e l = 512 , h = 8 d_{model}=512,h=8 dmodel=512,h=8,那么 d k = d v = d m o d e l / h = 64 d_k=d_v=d_{model}/h=64 dk=dv=dmodel/h=64。
四、Transformer
传统seq2seq的encoder跟decoder都是基于RNN等序列模型进行设计的,比如为了改善RNN的长期依赖问题,引入LSTM;为了获取目标端跟源端的对齐属性,引入了Attention机制。但是由于基础模型都是RNN等序列模型,在前向预测或者训练过程中,都是必须沿着序列方向依次进行计算(along the symbol positions),无法并行,因此计算效率是其面临的一个问题。为了改善这个问题,Google设计了Transformer特征抽取器。Transformer完全抛弃了RNN等序列模型,encoder跟decoder都是完全基于Attention机制设计的。
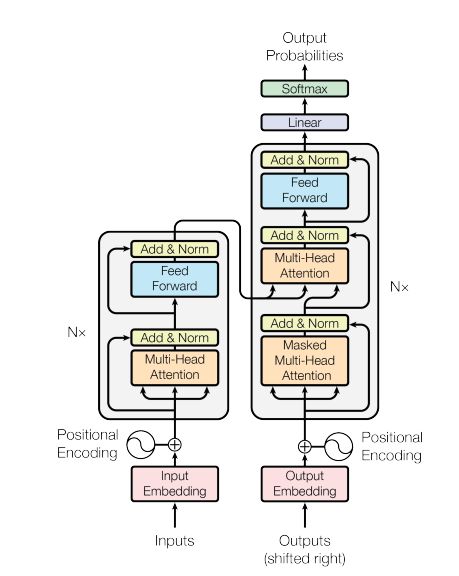
具体的模型结构如图17所示。整个网络结构还是沿用传统的两段式的encoder-decoder结构。
-
encoder跟decoder都是 N N N 层网络结构。对于encoder,每一层网络是由2个子层组成,分别是Multi-Head Attention跟Feed Forward Network。对于decoder,每一层网络则是由3个子层组成,分别是Masked Multi-Head Attention、Multi-Head Attention跟Feed Forward Network。除此之外,整个模型所有的子层都会引入残差连接以及layer normalization,因此每个子层的输出可以表示为 L a y e r N o r m ( x + S u b l a y e r ( x ) ) LayerNorm(x+Sublayer(x)) LayerNorm(x+Sublayer(x)),其中 x x x 表示每一个子层的输入。由于引入了残差连接,因此每一个子层网络的输出向量的维度都必须保持在 d m o d e l d_{model} dmodel。
-
Transformer网络除了encoder跟decoder之外,还包含embedding层跟softmax层。embedding层将输入或者输出的token转换成维度 d m o d e l d_{model} dmodel 的向量。softmax层将decoder输出的向量做一个线性变换然后经过softmax分类器,预测下一个token的概率值。这儿需要注意的是embding层也会做一个线性变化,跟softmax层的线性变化是共享权重参数的,只不过embedding层的权重参数会乘以一个缩放因子 d m o d e l \sqrt{d_{model}} dmodel。
-
为了充分利用序列的位置信息,Transformer在 embedding层引入了positional encoding。每一个token对应的positional encoding是一个 d m o d e l d_{model} dmodel 维的向量,表示如下: P E ( p o s , 2 i ) = s i n ( p o s / 1000 0 2 i / d m o d e l ) PE_{(pos,2i)}=sin(pos/10000^{2i/d_{model}}) PE(pos,2i)=sin(pos/100002i/dmodel) P E ( p o s , 2 i + 1 ) = c o s ( p o s / 1000 0 2 i / d m o d e l ) PE_{(pos,2i+1)}=cos(pos/10000^{2i/d_{model}}) PE(pos,2i+1)=cos(pos/100002i/dmodel)
-
Transformer总共有3种不同结构的Attention。在encoder中的Multi-Head Attention指的是典型的Attention,主要是为了捕捉源端词与词之间的依赖关系。Decoder有2种Attention。其中的Multi-Head Attention也是典型的Attention,只不过 K , V K,V K,V 是来自encoder,Q来自上一层decoder,主要是为了捕捉源端跟目标端词与词之间的依赖关系。Masked Multi-Head Attention是为了捕捉目标端词与词之间的依赖关系,加了Masked是为了防止信息泄露,也就是对下文序列的token做了一个掩码不可见的操作。
-
Transformer中的FFN是一个两层的全连接网络,而且是针对每一个position都是共享的。其计算公式如下: F F N ( x ) = m a x ( 0 , x W 1 + b 1 ) W 2 + b 2 FFN(x)=max(0,xW_1+b_1)W_2+b_2 FFN(x)=max(0,xW1+b1)W2+b2
-
关于并行,从上面的描述中可以看出,encoder始终是可并行的,也就是每个position之间的encoder计算可以说都是独立的。而对于decoder而言,训练时候,每个position可以看成是独立的,但在预测的时候,就依然还是不可并行计算的,当前position的计算还是得依赖上一个position的计算结果。
五、TransformerXL
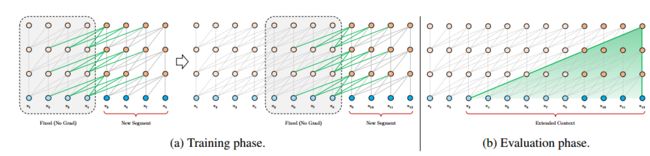
虽然Transformer在各项任务表现突出,但是其有一个比较明显的不足之处,也就是对长文本的长期依赖问题处理不好。首先Transformer的输入是固定长度的token序列,这就导致在训练的时候,经常需要对长文本进行固定片段的划分,分批进入网络训练,一方面是无法捕捉超长文本的依赖关系,另一方面也导致上下文碎片化,忽略了句子边界,也就是原文中提到的context fragmentation。因此,google在Transformer的基础上提出了TransformerXL(extra long的意思),目的就是为了解决Transformer在超长文本的不足之处,其改进点主要有两个:segment-level recurrence mechanism跟positional encoding scheme。
- segment-level recurrence mechanism(片段级递归机制)
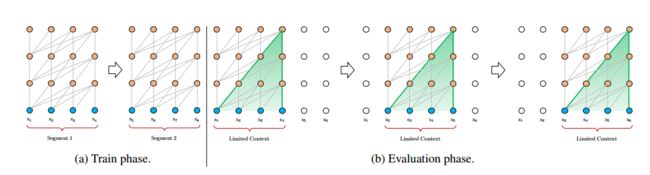
如图所示,Transformer在处理长文本时,都是通过设置滑动窗口来计算的,每一个窗口对应一个segment。虽然每一个窗口对每一个segment能够很好地处理上文依赖关系,但是窗口之间,也就是上下文segment之间的长期依赖信息并没能往后传递,而且每个窗口也可能会存在着依赖信息重复计算的情况(窗口重叠)。参考RNN获取长期依赖关系的方式,也就是通过同层间的隐状态进行传递,自然而然可以想到的方案就是给segment之间加入这种类似的机制。
假设相邻的两个长度为 L L L 的segment分别是 s τ = [ x τ , 1 , x τ , 2 , . . . , x τ , L ] s_\tau=[x_{\tau,1},x_{\tau,2},...,x_{\tau,L}] sτ=[xτ,1,xτ,2,...,xτ,L]、 s τ + 1 = [ x τ + 1 , 1 , x τ + 1 , 2 , . . . , x τ + 1 , L ] s_{\tau+1}=[x_{{\tau+1},1},x_{{\tau+1},2},...,x_{{\tau+1},L}] sτ+1=[xτ+1,1,xτ+1,2,...,xτ+1,L],每个segment在第 n n n 层的隐层状态是 h τ n ∈ R L ∗ d h_{\tau}^n\in R^{L*d} hτn∈RL∗d,其中 d d d 表示隐层状态的向量维度,那么TransformerXL的片段级递归机制可以表示为: h ^ τ + 1 n − 1 = [ S G ( h τ n − 1 ) ; h τ + 1 n − 1 ] \hat h_{\tau+1}^{n-1}=[SG(h_{\tau}^{n-1});h_{\tau+1}^{n-1}] h^τ+1n−1=[SG(hτn−1);hτ+1n−1] q τ + 1 n , k τ + 1 n , v τ + 1 n = h τ + 1 n − 1 W q T , h ^ τ + 1 n − 1 W k T , h ^ τ + 1 n − 1 W v T q_{\tau+1}^{n},k_{\tau+1}^{n},v_{\tau+1}^{n}=h_{\tau+1}^{n-1}W_q^T,\hat h_{\tau+1}^{n-1}W_k^T,\hat h_{\tau+1}^{n-1}W_v^T qτ+1n,kτ+1n,vτ+1n=hτ+1n−1WqT,h^τ+1n−1WkT,h^τ+1n−1WvT h τ + 1 n = T r a n s f o r m e r ( q τ + 1 n , k τ + 1 n , v τ + 1 n ) h_{\tau+1}^{n}=Transformer(q_{\tau+1}^{n},k_{\tau+1}^{n},v_{\tau+1}^{n}) hτ+1n=Transformer(qτ+1n,kτ+1n,vτ+1n) 由上可得, h τ n ∈ R L ∗ d h_{\tau}^n\in R^{L*d} hτn∈RL∗d 意味着memory只存储了长度为 L L L 的信息,理论上可以不加限制,因此广义的应该是 h ^ τ + 1 n − 1 = [ S G ( m τ n − 1 ) ; h τ + 1 n − 1 ] \hat h_{\tau+1}^{n-1}=[SG(m_{\tau}^{n-1});h_{\tau+1}^{n-1}] h^τ+1n−1=[SG(mτn−1);hτ+1n−1],其中 m τ n ∈ R M ∗ d m_{\tau}^n\in R^{M*d} mτn∈RM∗d。
- Relative Positional Encodings(相对位置编码)
Transformer采用一个固定的绝对位置向量矩阵 U ∈ R L m a x ∗ d U \in R^{L_{max}*d} U∈RLmax∗d 来表示位置信息。但对于片段递归机制而言,如果同一个position出现在相邻的两个segment中,那么是会有问题的,因此作者提出了相对位置编码的概念。先看看Transformer是怎么结合position coding做Attention score的计算,考虑绝对位置编码情况下,第 i i i 个query跟第 j j j 个key的score可以表示如下: A i , j a b s = ( ( E x i + U i ) W q ) T ( ( E x j + U j ) W k ) = E x i T W q T W k E x j ⎵ a + E x i T W q T W k U j ⎵ b + U i T W q T W k E x j ⎵ c + U i T W q T W k U j ⎵ d A_{i,j}^{abs}=((E_{x_i}+U_i)W_q)^T((E_{x_j}+U_j)W_k)\\=\underbrace{E_{x_i}^TW_q^TW_kE_{x_j}}_{a}+\underbrace{E_{x_i}^TW_q^TW_kU_j}_{b}+\underbrace{U_i^TW_q^TW_kE_{x_j}}_{c}+\underbrace{U_i^TW_q^TW_kU_j}_{d} Ai,jabs=((Exi+Ui)Wq)T((Exj+Uj)Wk)=a ExiTWqTWkExj+b ExiTWqTWkUj+c UiTWqTWkExj+d UiTWqTWkUj 其中 E E E 表示embedding。而考虑相对位置编码的情况,也就是TransformerXL,第 i i i 个query跟第 j j j 个key的score可以表示如下: A i , j r e l = E x i T W q T W k , E E x j ⎵ a + E x i T W q T W k , R R i − j ⎵ b + u T W k , E E x j ⎵ c + v T W k , R R i − j ⎵ d A_{i,j}^{rel}=\underbrace{E_{x_i}^TW_q^TW_{k,E}E_{x_j}}_{a}+\underbrace{E_{x_i}^TW_q^TW_{k,R}R_{i-j}}_{b}+\underbrace{u^TW_{k,E}E_{x_j}}_{c}+\underbrace{v^TW_{k,R}R_{i-j}}_{d} Ai,jrel=a ExiTWqTWk,EExj+b ExiTWqTWk,RRi−j+c uTWk,EExj+d vTWk,RRi−j 对比绝对位置编码,区别主要有:在b、d项,引入了 R ∈ R L m a x ∗ d R \in R^{L_{max}*d} R∈RLmax∗d 表示的是相对位置差的向量编码,该矩阵类似原来的 U U U 不需要训练得到的;在c、d项,引入 u , v u,v u,v 主要想通过可训练的参数获取统一的表达,因为query对所有position是一样的,不需要位置信息;在a、b、c、d项,将 W k W_k Wk 拆分成两个 W k , E W_{k,E} Wk,E, W k , R W_{k,R} Wk,R,分别对应产生content-based的key以及location-based的key。因此,最后a、b、c、d分别对应的就是content-based addressing、content-dependent positional bias、global content bias、global positional bias。
六、Pretrain + Finetune Pipeline
(一)ELMo
通过预训练得到高质量的词向量一直是具有挑战性的问题,主要有两方面的难点,一个是词本身具有的语法语义复杂属性,另一个是这些语法语义的复杂属性如何随着上下文语境产生变化,也就是一词多义性问题。传统的词向量方法例如word2vec、GloVe等都是训练完之后,每个词向量就固定下来,这样就无法解决一词多义的问题。为了解决这个问题,AI2提出了ELMo(Embeddings from Language Models),其通过在大型语料上预训练一个深度BiLSTM语言模型网络来获取词向量,也就是每次输入一句话,可以根据这句话的上下文语境获得每个词的向量,这样子就可以解决一词多义问题。总结来说,word2vec、GloVe等模型是得到一个大型的词向量矩阵,每个词的向量都是固定的,而ELMo是得到一个预训练的语言模型,每次需要获取一个词的向量时,需要实时输入词的上下文序列,从而得到该语境下的词向量。
除此之外,ELMo是一个多层的网络结构,最终得到的词向量可以是每一层网络输出向量的线性组合,而不仅仅只是顶层输出的向量。通过评估可以发现,底层网络的输出向量主要获取语法层面的信息,因此在词性标注等任务表现突出;而顶层网络的输出向量主要获取上下文相关的语义信息,因此在词义消岐等任务表现突出。
1、双向LSTM语言模型
-
前向LSTM语言模型表达式如下: p ( t 1 , t 2 , . . . , t N ) = ∏ k = 1 N p ( t k ∣ t 1 , t 2 , . . . , t k − 1 ) p(t_1,t_2,...,t_N)=\prod_{k=1}^Np(t_k|t_1,t_2,...,t_{k-1}) p(t1,t2,...,tN)=k=1∏Np(tk∣t1,t2,...,tk−1)
其中 t k t_k tk 表示第 k k k 个token,在输入层,会转换成与上下文无关的词向量 x k L M x_k^{LM} xkLM(原文作者用的是CNN-BIG-LSTM);前向LSTM模型一共有 L L L 层隐层,第 k k k 个token在第 j j j 层的状态值为: h → k , j L M \stackrel{\rightarrow}{h}_{k,j}^{LM} h→k,jLM,而第 k k k 个token在第 L L L 层的状态值 h → k , L L M \stackrel{\rightarrow}{h}_{k,L}^{LM} h→k,LLM,后面一般会接一个softmax,用来预测 t k + 1 t_{k+1} tk+1。 -
后向LSTM语言模型表达式如下: p ( t 1 , t 2 , . . . , t N ) = ∏ k = 1 N p ( t k ∣ t k + 1 , t k + 2 , . . . , t N ) p(t_1,t_2,...,t_N)=\prod_{k=1}^Np(t_k|t_{k+1},t_{k+2},...,t_N) p(t1,t2,...,tN)=k=1∏Np(tk∣tk+1,tk+2,...,tN) 后向LSTM模型跟前向LSTM模型结构类似,只是方向相反,第 k k k 个token在第 j j j 层的状态值表示为: h ← k , j L M \stackrel{\leftarrow}{h}_{k,j}^{LM} h←k,jLM
-
双向LSTM语言模型:其实就是对前向LSTM语言模型跟后向LSTM语言模型做一个联合训练。损失函数定义如下: ∑ k = 1 N ( l o g p ( t k ∣ t 1 , t 2 , . . . , t k − 1 ; θ x , θ → L S T M , θ s ) + l o g p ( t k ∣ t k + 1 , t k + 2 , . . . , t N ; θ x , θ ← L S T M , θ s ) ) \sum_{k=1}^N(logp(t_k|t_1,t_2,...,t_{k-1};\theta_x,\stackrel{\rightarrow}{\theta}_{LSTM},\theta_s)+logp(t_k|t_{k+1},t_{k+2},...,t_N;\theta_x,\stackrel{\leftarrow}{\theta}_{LSTM},\theta_s)) k=1∑N(logp(tk∣t1,t2,...,tk−1;θx,θ→LSTM,θs)+logp(tk∣tk+1,tk+2,...,tN;θx,θ←LSTM,θs)) 其中 θ x \theta_x θx 表示embedding层的参数,将token转换成上下文无关的输入词向量。 θ s \theta_s θs 表示softmax的参数,这两个参数在前向跟后向网络是共享的。而 θ → L S T M \stackrel{\rightarrow}{\theta}_{LSTM} θ→LSTM 跟 θ ← L S T M \stackrel{\leftarrow}{\theta}_{LSTM} θ←LSTM 分别表示前向跟后向网络的模型参数。
2、ELMo向量
对于一个token t k t_k tk,在一个 L L L 层的双向LSTM模型中,其有一套 2 L + 1 2L+1 2L+1 的向量表示组合: R k = { x k L M , h → k , j L M , h ← k , j L M ∣ j = 1 , 2 , . . . , L } R_k= \{x_k^{LM},\stackrel{\rightarrow}{h}_{k,j}^{LM},\stackrel{\leftarrow}{h}_{k,j}^{LM}|j=1,2,...,L\} Rk={xkLM,h→k,jLM,h←k,jLM∣j=1,2,...,L} 可以将每一层的前向跟后向隐层向量进行维度上的拼接,从而得到 L + 1 L+1 L+1 个向量表示组合: R k = { h k , j L M ∣ j = 0 , 1 , 2 , . . . , L } R_k=\{h_{k,j}^{LM}|j=0,1,2,...,L\} Rk={hk,jLM∣j=0,1,2,...,L} 其中 h k , j L M = [ h → k , j L M ; h ← k , j L M ] h_{k,j}^{LM}=[\stackrel{\rightarrow}{h}_{k,j}^{LM};\stackrel{\leftarrow}{h}_{k,j}^{LM}] hk,jLM=[h→k,jLM;h←k,jLM] 当 j = 0 j=0 j=0 时, h k , 0 L M = [ x k L M ; x k L M ] h_{k,0}^{LM}=[x_k^{LM};x_k^{LM}] hk,0LM=[xkLM;xkLM] 表示输入层。那么ELMo向量可以表示如下: E L M o k t a s k = E ( R k ; θ t a s k ) = γ t a s k ∑ j = 0 L s j t a s k h k , j L M ELMo_k^{task}=E(R_k;\theta^{task})=\gamma^{task}\sum_{j=0}^Ls_j^{task}h_{k,j}^{LM} ELMoktask=E(Rk;θtask)=γtaskj=0∑Lsjtaskhk,jLM 其中 s j t a s k s_j^{task} sjtask 是跟任务相关的softmax权重参数, γ t a s k \gamma^{task} γtask 是一个缩放因子,这两个参数在ELMo向量的实际应用中属于工程性的trick。
3、ELMo向量在下游监督任务的应用
基于一个预训练好的BiLSTM语言模型,我们可以得到一套 2 L + 1 2L+1 2L+1 的向量表示组合(一般取 L = 2 L=2 L=2,那么就可以得到3层向量特征,可以理解为输入层捕捉的是单词特征,第一层LSTM捕捉的是句法信息,第二层LSTM捕捉的是语义信息),那么只需要结合下游任务,学习获得权重因子 s j t a s k s_j^{task} sjtask、 γ t a s k \gamma^{task} γtask 即可得到最终的词向量 E L M o k t a s k ELMo_k^{task} ELMoktask。
ELMo的作者提供了几种应用的思路:(1)固定权重因子 s j t a s k s_j^{task} sjtask、 γ t a s k \gamma^{task} γtask,从而得到 E L M o k t a s k ELMo_k^{task} ELMoktask 向量,然后跟原始词向量进行拼接, [ x k ; E L M o k t a s k ] [x_k;ELMo_k^{task}] [xk;ELMoktask],再输入到下游任务中,重新训练权重因子。(2)在前者的基础上,对隐层的输出也引入ELMo向量, [ h k ; E L M o k t a s k ] [h_k;ELMo_k^{task}] [hk;ELMoktask],只不过是采用不同的权重因子。
(二)GPT
ELMo虽然解决了一词多义的问题,但还有没有改善的空间呢?肯定是有的,最简单的想法就是用新秀特征抽取器Transformer替换LSTM,因此,openAI就提出了GPT(Generative Pre-Training)。基于Pretrain + Finetune范式,用Transformer decoder替换ELMo的LSTM,而且GPT只采取了单向的网络,这儿也就埋下了伏笔,给了Bert有机可乘(Bert后面再介绍)。
-
前向计算:对于输入的第 i i i 个token,其上文长度为 k k k 的token序列可以表示为 U = ( u − k , . . . , u − 2 , u − 1 ) U=(u_{-k},...,u_{-2},u_{-1}) U=(u−k,...,u−2,u−1),因此GPT的前向计算可以表示如下: h 0 = U W e + W p h_0=UW_e+W_p h0=UWe+Wp h l = T r a n s f o r m e r _ b l o c k ( h l − 1 , i = 1 , 2 , . . , n ) h_l=Transformer\_block(h_{l-1} ,i=1,2,..,n) hl=Transformer_block(hl−1,i=1,2,..,n) P ( u ) = s o f t m a x ( h n W e T ) P(u)=softmax(h_nW_e^T) P(u)=softmax(hnWeT) 总共有 n n n 层网络, W e W_e We 表示embedding矩阵, W p W_p Wp 表示position encoding; h l h_l hl 表示第 l l l 层Transformer的输出; Transformer_block用的是传统的Transformer中的decoder(当然,没有了encoder,就不需要Multi-Head Attention,只需要Masked Multi-Head Attention跟FFN即可)。
-
Pretrain:GPT的预训练是基于以下的损失函数进行梯度下降训练(单向语言模型): L 1 ( μ ) = ∑ i l o g P ( u i ∣ u i − k , . . . , u i − 1 ; θ ) L_1(\mu)=\sum_ilogP(u_i|u_{i-k},...,u_{i-1};\theta) L1(μ)=i∑logP(ui∣ui−k,...,ui−1;θ) 其中 μ = ( u 1 , u 2 , . . . , u m ) \mu=(u_1,u_2,...,u_m) μ=(u1,u2,...,um) 表示输入token序列。
-
Finetune:假设现有数据集 C = ( x , y ) C=(x,y) C=(x,y),下游任务是一个分类任务,那么其预测函数为: P ( y ∣ x 1 , x 2 , . . . , x m ) = s o f t m a x ( h n m W y ) P(y|x_1,x_2,...,x_m)=softmax(h_n^mW_y) P(y∣x1,x2,...,xm)=softmax(hnmWy)其中 x m x_m xm 表示第 m m m 个token, W y W_y Wy 表示接在最后一个token后面的线性转换矩阵, h n m h_n^m hnm 表示第 m m m 个token在第 n n n 个Transformer的输出。最终Finetune时候的损失函数可以定义为: L 3 ( C ) = L 2 ( C ) + λ ∗ L 1 ( C ) L_3(C)=L_2(C)+\lambda*L_1(C) L3(C)=L2(C)+λ∗L1(C) L 2 ( C ) = ∑ ( x , y ) l o g P ( y ∣ x 1 , x 2 , . . . , x m ) L_2(C)=\sum_{(x,y)}logP(y|x_1,x_2,...,x_m) L2(C)=(x,y)∑logP(y∣x1,x2,...,xm)
(三)BERT
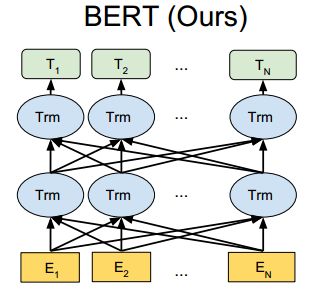
前面提到的GPT是基于单向语言模型来做预训练的,在sentence级别的NLP任务表现良好,但是在token级别的NLP任务并不是最佳选择,毕竟token的含义不仅取决于上文信息,同时也跟下文信息有着密切关系,因此,Google提出了BERT(Bidirectional Encoder Representations from Transformers)模型,用双向语言模型替换单向语言模型。
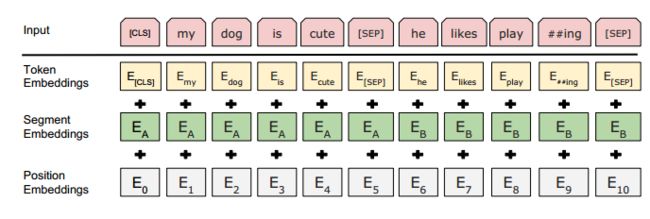
- 前向计算:如图可以看出,BERT的前向跟GPT的前向区别主要有两点:(1)GPT的特征抽取器采用的是Transformer的decoder(单向语言模型),而BERT采用的是Transformer的encoder(双向语言模型);(2)输入表示的区别:如图23所示,所有输入序列开头添加[CLS]token(对于N vs 1的NLP下游任务,取[CLS]token的最后一层向量进入下游任务),句子结尾添加[SEP]token;输入层由3个embedding向量组成,分别是token embedding、segment embedding、position embedding;输入token不超过512个。
-
Pretrain:区别于GPT的单向语言模型训练,BERT是一个双向语言模型,作者采用两个无监督任务进行预训练,一个是token级别的,一个是sentence级别。token级别的预训练任务采用的是Masked Language Model(MLM);具体做法是取每个输入序列15%的token进行预测,其中80%替换成[mask],10%替换成随机token,10%保持不变;训练过程中,在这15%的token的最后一层向量后面接一层softmax进行预测。sentence级别的预训练任务采用的是next sentence predict;具体做法就是构造句子对训练样本 [ s e n t e n c e A , s e n t e n c e B ] [sentence_A,sentence_B] [sentenceA,sentenceB],50%的样本label为1,表示句子B是句子A的下一句,50%的样本label为0,表示句子B不是句子A的下一句;训练过程中,取[CLS]token的最后一层向量进行预测。因此,BERT就是联合上述两个任务进行预训练的,既可以捕捉token级别的信息,又可以捕捉sentence级别的信息。
-
Finetune:BERT的Finetune就很好理解了,跟GPT的Finetue没有太大区别,都是采用少量的NLP下游任务的监督样本,对BERT以及下游任务的参数进行微调。
(四)GPT2.0
前文提到的ELMo、GPT、BERT本质上都是基于大量无监督样本的预训练以及少量指定任务的有监督样本进行Finetune,最终衡量各个预训练模型的效果都是通过在各种下游任务的benchmark刷SOA来验证。而GPT2.0则不是一味地刷benchmark的SOA来指导工作,其更关注的是预训练模型的通用性。原文作者提出,现有的机器学习系统更多的像是一个narrow experts,在指定领域,拥有数量足够大的标注数据集、容量足够大的模型结构,在有监督的学习方法下,就可以获得特定领域下足够好的效果;但这些模型对数据的分布比较敏感而且现实世界中,很多特定领域的任务都没有足够多的标注样本;所以作者把研究的重心放在了competent generalists,也就是通过无监督的方法获取更加通用的模型上,通用到不需要有监督的Finetune就可以直接应用到下游任务中。论文作者也提出了,现有模型缺乏的泛化能力主要是因为训练过程中的单任务单领域数据所导致。因此,GPT2.0更加关注的是通过多领域的数据集来获取更加通用的预训练模型(multi-task learning),从而在zero-shot(无需任务参数以及网络结构的调整)的设定下,可以在下游任务中表现良好。
相比GPT,GPT2.0的改进在于:
-
对GPT的模型参数进行扩容:比如扩充到48层的Transformer Layer;将Layer Normalization放到每一层的外面;将输入token序列长度由512的限制扩充到1024等。
-
更丰富、更高质量的数据集:通过爬取网页,人工筛选,最终构建了800万篇、40GB大小的网页数据集WebText。
-
单向语言模型+多任务的训练方法:GPT的单向语言模型可以表示为 p ( o u t p u t ∣ i n p u t ) p(output|input) p(output∣input),而GPT2.0则是在单向语言模型的基础上,加入了多任务的因素, p ( o u t p u t ∣ i n p u t , t a s k ) p(output|input,task) p(output∣input,task)。具体是通过构造训练样本而实现的,在输入的token序列添加具体的任务标识(下游任务通过任务标识来做预测),比如对于翻译任务,输入token序列可以表示为: ( t r a n s l a t e t o f r e n c h , e n g l i s h t e x t , f r e n c h t e x t ) (translate\ to\ french,english\ text,french\ text) (translate to french,english text,french text),对于阅读理解任务,输入token序列可以表示为: ( a n s w e r t h e q u e s t i o n , d o c u m e n t , q u e s t i o n , a n s w e r ) (answer\ the\ question,document,question,answer) (answer the question,document,question,answer)。
-
基于Byte Pair Encoding的输入表示。
(五)XLNet
前面提到的GPT跟BERT这两个语言模型,分别属于AutoRegressive(AR)模型跟denoising AutoEncoder(AE)模型。其中AR模型属于单向语言模型,可以表示为: p ( x ) = ∏ t = 1 T p ( x t ∣ x < t ) p(x)=\prod_{t=1}^Tp(x_t|x_{<t}) p(x)=∏t=1Tp(xt∣x<t);而AE模型没有明确的density estimation,其通过对输入token序列随机做[MASK](denoising的体现),然后再进行重建,从而训练得到整个语言模型,属于双向语言模型,可以获得上下文信息。可以分别看一下AR模型跟AE模型的似然函数,对于AR模型,其最大似然函数表示为: m a x θ l o g p θ ( x t ∣ x < t ) = ∑ t = 1 T l o g e x p ( h θ ( x 1 : t − 1 ) T e ( x t ) ) ∑ x ′ e x p ( h θ ( x 1 : t − 1 ) T e ( x ′ ) ) max_\theta\ logp_\theta(x_t|x_{<t})=\sum_{t=1}^Tlog\frac{exp(h_\theta(x_{1:t-1})^Te(x_t))}{\sum_{x^{'}}exp(h_\theta(x_{1:t-1})^Te(x^{'}))} maxθ logpθ(xt∣x<t)=t=1∑Tlog∑x′exp(hθ(x1:t−1)Te(x′))exp(hθ(x1:t−1)Te(xt)) 其中 e e e 表示embedding向量;对于AE模型,假设 x − \stackrel{-}{x} x− 表示被mask的token, x ^ \hat{x} x^ 则表示被mask后的完整token序列,那么其最大似然函数可以表示为: m a x θ l o g p ( x − ∣ x ^ ) ≈ ∑ t = 1 T m t l o g p θ ( x t ∣ x ^ ) = ∑ t = 1 T m t l o g e x p ( H θ ( x ^ ) t T e ( x t ) ) ∑ x ′ e x p ( H θ ( x ^ ) t T e ( x ′ ) ) max_\theta\ logp(\stackrel{-}{x}|\hat{x})\approx\sum_{t=1}^Tm_tlogp_{\theta}(x_t|\hat{x})=\sum_{t=1}^Tm_tlog\frac{exp(H_\theta(\hat{x})_t^Te(x_t))}{\sum_{x^{'}}exp(H_\theta(\hat{x})_t^Te(x^{'}))} maxθ logp(x−∣x^)≈t=1∑Tmtlogpθ(xt∣x^)=t=1∑Tmtlog∑x′exp(Hθ(x^)tTe(x′))exp(Hθ(x^)tTe(xt)) 其中 m t = 1 m_t=1 mt=1 表示被maske的token。
基于AR的GPT模型缺点在于只能学到上文信息;而基于AE的BERT模型虽然可以学到上下文信息,但由于训练时对输入token序列随机做了[MASK],导致了Pretrain跟Finetune两个阶段输入不一致,而且随机替换token,会破坏masked token之间的相关性(例如对“因为”、“所以”这样一些具有上下文关系的masked token),对于某些特定任务,效果不佳。而为了综合AE跟AR的优点,google提出了XLNet。XLNet本质上是一个AR模型,但其通过优化联合概率分布函数的所有可分解排列组合的期望似然(排列语言模型)引入上下文信息,除此之外,也集成了TransformerXL(当前效果最好的AR模型)的优点segment-level recurrence mechanism
跟positional encoding scheme,解决长文本依赖问题,从而完虐BERT。
- Permutation Language Modeling(排列语言模型)
对于AR模型的表达 p ( x ) = ∏ t = 1 T p ( x t ∣ x < t ) p(x)=\prod_{t=1}^Tp(x_t|x_{<t}) p(x)=∏t=1Tp(xt∣x<t),其通过将联合概率分布拆解成多个条件概率的累积,默认是前向的分解方式,也就是 p ( x ) = ∏ t = 1 T p ( x 1 ) p ( x 2 ∣ x 1 ) p ( x 3 ∣ x 1 , x 2 ) , . . . , p ( x T ∣ x < T ) p(x)=\prod_{t=1}^Tp(x_1)p(x_2|x_1)p(x_3|x_1,x_2),...,p(x_T|x_{<T}) p(x)=∏t=1Tp(x1)p(x2∣x1)p(x3∣x1,x2),...,p(xT∣x<T)。但其实是可以有 T ! T! T! 种分解方式,如图24,对于输入序列 x 1 , x 2 , x 3 , x 4 {x_1,x_2,x_3,x_4} x1,x2,x3,x4,列举了4种分解的方式(例如对于分解顺序2-4-3-1, p ( x ) = ∏ t = 1 4 p ( x 2 ) p ( x 4 ∣ x 2 ) p ( x 3 ∣ x 2 , x 4 ) p ( x 1 ∣ x 2 , x 4 , x 3 ) p(x)=\prod_{t=1}^4p(x_2)p(x_4|x_2)p(x_3|x_2,x_4)p(x_1|x_2,x_4,x_3) p(x)=∏t=14p(x2)p(x4∣x2)p(x3∣x2,x4)p(x1∣x2,x4,x3))。假设 Z T Z_T ZT 表示所有分解方式的集合, z z z 表示具体的分解方式,那么排列语言模型的最大化期望似然可以表示为: m a x θ E z ∼ Z T [ ∑ t = 1 T l o g p θ ( x z t ∣ x z < t ) ] max_\theta\ E_{z\sim{Z_T}}[\sum_{t=1}^Tlogp_\theta(x_{z_t}|x_{z<t})] maxθ Ez∼ZT[t=1∑Tlogpθ(xzt∣xz<t)] 如式子所示,所有分解方式都共享一套模型参数,最终的优化目标就是所有分解方式的期望似然。这儿需要注意的是:(1)排列语言模型并没有改变输入token序列的顺序,而是改变分解的顺序(通过Transformer内部Attention的掩码来实现),这点很重要,因为在Finetune阶段,模型的输入是有序的。(2)不一定需要采集所有的分解方式,可以用采样的方式。
- Two-Stream Self-Attention(双流自注意模型)
基于Transformer来实现排列语言模型,其概率函数可以表示如下: p θ ( x z t = x ∣ x z < t ) = e x p ( h θ ( x z < t ) T e ( x ) ) ∑ x ′ e x p ( h θ ( x z < t ) T e ( x ′ ) ) p_\theta(x_{z_t}=x|x_{z<t})=\frac{exp(h_\theta(x_{z<t})^Te(x))}{\sum_{x^{'}}exp(h_\theta(x_{z<t})^Te(x^{'}))} pθ(xzt=x∣xz<t)=∑x′exp(hθ(xz<t)Te(x′))exp(hθ(xz<t)Te(x)) 其中 z z z 表示某种分解的顺序, h θ ( x z < t ) h_\theta(x_{z<t}) hθ(xz<t) 表示 t t t 时刻之前的上文信息;根据式子可以看出,预测函数跟token所在位置无关,也就是对target position不敏感,从而丢失了位置信息,导致训练得到的representation没有多大意义(假设输入token序列是 x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1,x2,x3,x4,对于分解顺序1-2-3-4跟1-2-4-3,在位置3跟4看到的都是位置1跟2,由于没有位置信息 z t z_t zt,大家看到的都是位置1跟2,所以就会给训练带来不确定性,这个不确定性是排列语言模型带来的,GPT中由于只有前向一种分解方式,因而没有这个问题的存在)。为了避免这个问题,原文作者对预测函数做了re-parameterize,表示如下: p θ ( x z t = x ∣ x z < t ) = e x p ( g θ ( x z < t , z t ) T e ( x ) ) ∑ x ′ e x p ( g θ ( x z < t , z t ) T e ( x ′ ) ) p_\theta(x_{z_t}=x|x_{z<t})=\frac{exp(g_\theta(x_{z<t},z_t)^Te(x))}{\sum_{x^{'}}exp(g_\theta(x_{z<t},z_t)^Te(x^{'}))} pθ(xzt=x∣xz<t)=∑x′exp(gθ(xz<t,zt)Te(x′))exp(gθ(xz<t,zt)Te(x)) 其中 g θ ( x z < t , z t ) g_\theta(x_{z<t},z_t) gθ(xz<t,zt) 引入了target position信息 z t z_t zt。虽然通过引入位置变量 z t z_t zt 可以获取target-aware的表达,但是怎么设计 g θ ( x z < t , z t ) g_\theta(x_{z<t},z_t) gθ(xz<t,zt) 成了一个难题。原文作者提出了双流的概念,如图25所示(结合图24的(a)(b)小图)。双流指的分别是query stream跟content stream:
其中 g z t ( m ) g_{z_t}^{(m)} gzt(m) 表示第 m m m 层的 g θ ( x z < t , z t ) g_\theta(x_{z<t},z_t) gθ(xz<t,zt);而 h z t ( m ) h_{z_t}^{(m)} hzt(m) 则表示第 m m m 层的 h θ ( x z ≤ t ) h_\theta(x_{z\leq{t}}) hθ(xz≤t)。其中content stream跟传统的Transformer的Attention机制一样,而QS(query stream)跟CS(content stream)的区别联系就在于:QS的K、V是来自CS;QS只包含当前位置信息 z t z_t zt(体现在 Q = g z t m − 1 Q=g_{z_t}^{m-1} Q=gztm−1,其实就是通过设计一个包含 z t z_t zt 的Q),不包含 x z t x_{z_t} xzt,而CS除了包含 z t z_t zt,还包含了 x z t x_{z_t} xzt。
总结
本文主要是对Pretain+Finetune范式下的若干主流模型进行一个学习总结,基本都是抱着论文一步一步啃下来的,至于在实际业务中的落地效果,下来笔者再持续关注。
作者简介
zakexu,硕士毕业于华南理工大学,现任腾讯云AI算法工程师,负责腾讯云NLP的公有云产品架构以及标准化产品交付,欢迎交流合作!
- 个人博客:https://zakexu.blog.csdn.net/
- 知乎ID:zakexu
参考文献
- Understanding LSTM Networks
- 完全图解RNN、RNN变体、Seq2Seq、Attention机制
- 模型汇总24 - 深度学习中Attention Mechanism详细介绍:原理、分类及应用
- Attention Is All You Need
- Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context
- Deep contextualized word representations
- Improving Language Understanding by Generative Pre-Training
- BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding
- Language Models are Unsupervised Multitask Learners
- XLNet: Generalized Autoregressive Pretraining for Language Understanding