【图论】强连通分量和拓扑排序

说实话，这个标题是我实在不知道起什么名字了，强拓其实比较简单，篇幅也会短一点……

====================分割线==================

水题一道引入：
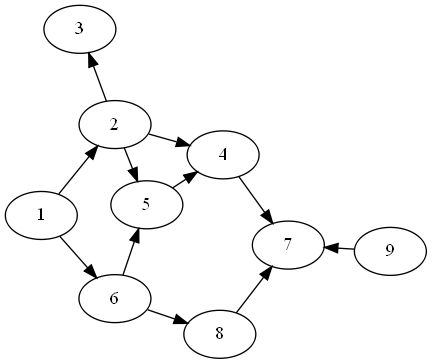
给出一列城市，编号1~n，每个城市有不同价值的宝藏。有m条道路，每个城市只有通向编号比它大的城市的道路。现在你可以从任意一个城市进入，从任意一个城市出来，请找出一条路线，使经过的城市的宝藏价值之和最大？

这道题如果不考虑数据范围，想到的显然是dp，因为题目中提到【只有通向编号比它大的城市的道路】。也就是说，可以从前往后推，这样很容易写出递推式：

f[i]=max(f[j]+way[j][i])
way[j][i]表示从j到i的距离。
答案就是： max(f[1..n])

但若是我们可以从编号大的往小的走呢？比如：

显然我们是不能直接dp的了。但根据以往的经验，我们可以想到一种叫拓扑排序的东西，来确定我们dp的顺序。什么是拓扑排序呢？就是：

每次寻找入度为0的点，加入序列中
删掉它的出边
重复以上操作
直至所有点都加入了序列

当然，这种排序如果暴力写，时间复杂度要多一个n，为了找入度为0的点。实际上，当我们每次找完一个点，就可以把与这个点相连的所有点的入度都减一，如果此时那个点入度为零就加进去，否则不管。
拓扑排序的时间复杂度是 O(n+m) ，即点数加边数。

好吧，其实上面这种图有专业术语：
有向无环图/拓扑图/DAG
都一样……哪个比较装用哪个好啦~

那么问题来了，如果图变成有环了的呢？又该怎么处理，就像这样：

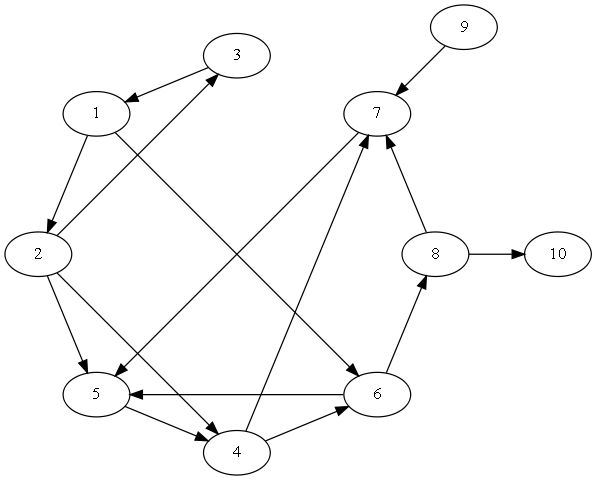
当然，通过以前学的并查集我们很容易想到，一个环就是一个集合，我们可以把这个集合看做是一个点。但如何知道哪些点是一个集合？又怎样处理与之相连的边呢？

这就是今天要讲的强连通分量了！
比如上图中的1、2、3三个城市，是可以互相到达的，我们就称它为连通分量，而现在这个连通分量又是不可能更大（没有其他城市与它们互相到达），我们就称之为强连通分量。

首先我们考虑搜索树，这样我们可以得到这样一幅图：

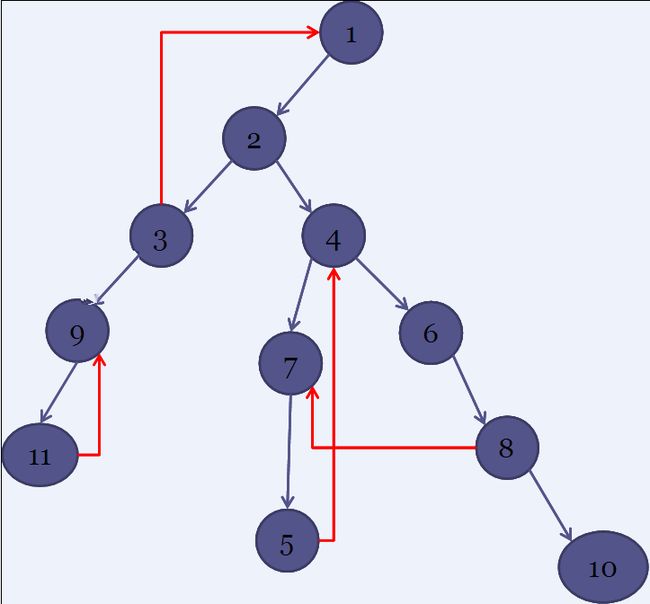
我们把强连通分量圈起来，就是这样的：

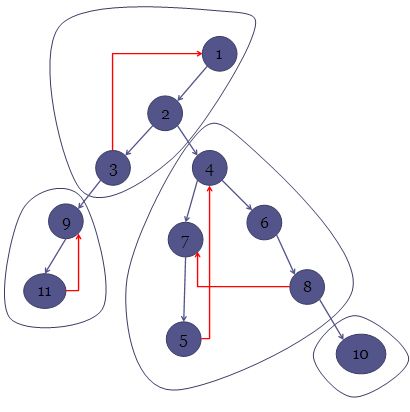
那么让我们来思考为什么是这样子的？为什么强连通分量都是在同一棵子树上呢？
显然，因为dfs的性质，如果能相连，必然在其子节点……于是我们就可以简化问题，用dfs来做，只用找到每个强连通分量的开始与结束就行了。

DFS时我们维护两个数组dfn[],low[]
dfn[i]是i点的进入时间
low[i]是从i点出发，所能访问到的最早的进入时间

那怎么维护呢？这里我不想多说，拿样例大概就是，首先一路往下搜，搜到3，发现它可以搜到1，但是1比它早，所以我们把low[3]改成low[1]，然后再继续往下。回溯的时候，我们发现有一个节点的dfn和low一样，我们就可以知道low是这个值的节点属于一个强连通分量，我们可以用栈来帮助存储。
伪代码：

DFS(u)
dfn[u] = low[u] = ++Time
    stack.push(u)
state[u]=1 //已访问并入栈
for v 是u的一条出边的端点
    if (state[v] == 0) //未访问
        DFS(v)
    low[u] = min(low[u],  low[v])
    if (state[v] == 1)
        low[u] = min(low[u], low[v])

if (dfn[u] == low[u])
stack.pop() until 弹出了u //这些点构成一个强连通分量
弹出的点的state[] = 2

那么还有一个问题，就是处理出来的新图怎么连边？显然，直接连就好……