无聊写排序之 ----部分排序(Partial Sort)

当有一个无序的序列集合的时候，我们想知道这个序列里面按照某种排序关系最大的m个或者前top个有序的元素。比如我又100个学生，我只想知道排名前20的学生的名次列表，剩余的我并不关心，如何去得到呢？ 当然你脑海中第一个闪过的便是sort，做一次排序，取排序后前面的20不就好了吗？ 没错，排序作为做常规的方法，肯定是最先想到的，这里要介绍的是比排序来的更快更直接的一个算法：部分排序（partial_sort）,该算法来自于STL的算法库，在研究STL源码时看到的，瞬间眼前一亮，这里分享出来。

partial_sort算法接受一个middle的index，该middle位于[first, last)的元素序列范围内，然后重新安排[first, last),使得序列中的middle-first个最小元素以指定顺序排序最终放置在[first, middle)中， 其余的元素安置在[middle, last)内，不保证有任何指定的顺序。因此可以看出来partial_sort执行后并不保证所有的结果都有序，而有序的部分数量永远都小于等于整个元素区间的数量。所以在只是挑出前m个元素的排序中，效率明显要高于全排序的sort算法，当然m越小效率越高，m等于n时相当于全排序了。

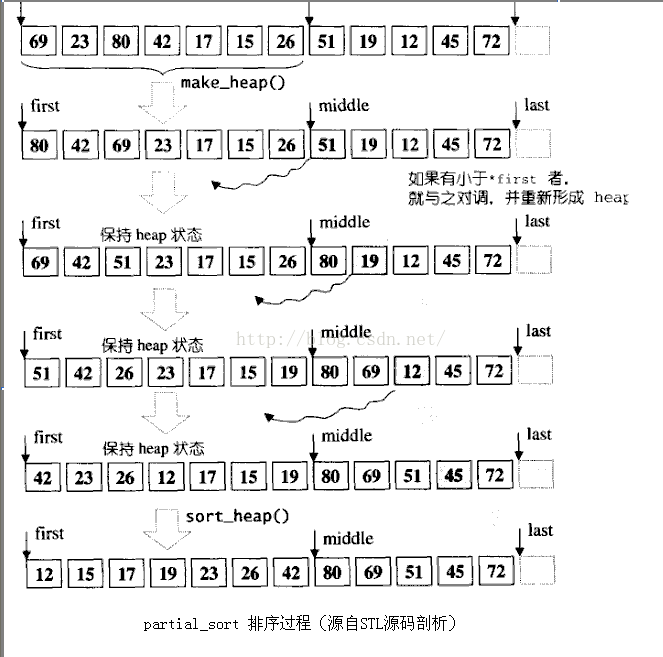
partial_sort的原理：部分排序的原型出现在STL的算法库里面，根据其所描述的代码，很容易可以看出来partial_sort是借用了堆排序的思想来作为底层排序实现的。对于该算法的原理这样描述。假设我们有n个元素序列，需要找到其中最小的m个元素，m<=n时。 先界定区间[first, m) 然后对该区间使用make_heap()来组织成一个大顶堆。然后遍历剩余区间[m, last)中的元素， 剩余区间的每个元素均与大顶堆的堆顶元素进行比较（大顶堆的堆顶元素为最大元素，该元素为第一个元素，很容易获得），若堆顶元素较小，边交换堆顶元素和遍历得到的元素值，重新调整该大顶堆以维持该堆为大顶堆。遍历结束后，[first, m)区间内的元素便是排名在前的m个元素，在对该堆做一次堆排序便可得到最好的结果。

                 

算法使用演示如下：

#include 
#include 
#include 
#include 
using namespace std;

int main()
{
	vector vc;
	for (int i = 0; i < 10; i++)
	{
		vc.push_back(rand()%100);
	}

 	for (int i = 0; i < vc.size(); i++)
		cout << vc[i] << " ";
 	cout << endl;

	partial_sort(vc.begin(), vc.begin()+4, vc.end());

	for (int i = 0; i < vc.size(); i++)
		cout << vc[i] << " ";
	cout << endl;

	return 0;
}

运行结果：

STL源码：

template 
inline void partial_sort(RandomAccessIterator first,
	RandomAccessIterator middle,
	RandomAccessIterator last) {
		__partial_sort(first, middle, last, value_type(first));
}

template 
void __partial_sort(RandomAccessIterator first, RandomAccessIterator middle,
	RandomAccessIterator last, T*) {
		make_heap(first, middle); //将区间[first, middle)构造为一个堆结构
		for (RandomAccessIterator i = middle; i < last; ++i)
			if (*i < *first)    // 遍历堆以外的元素，并将更优的元素放入堆中
				__pop_heap(first, middle, i, T(*i), distance_type(first));
		sort_heap(first, middle); // 对最终的堆进行排序
}

heap源码：

template 
inline void partial_sort(RandomAccessIterator first,
	RandomAccessIterator middle,
	RandomAccessIterator last) {
		__partial_sort(first, middle, last, value_type(first));
}

template 
void __partial_sort(RandomAccessIterator first, RandomAccessIterator middle,
	RandomAccessIterator last, T*) {
		make_heap(first, middle); //将区间[first, middle)构造为一个堆结构
		for (RandomAccessIterator i = middle; i < last; ++i)
			if (*i < *first)    // 遍历堆以外的元素，并将更优的元素放入堆中
				__pop_heap(first, middle, i, T(*i), distance_type(first));
		sort_heap(first, middle); // 对最终的堆进行排序
}

template 
inline void make_heap(RandomAccessIterator first, RandomAccessIterator last) {
	__make_heap(first, last, value_type(first), distance_type(first));
}

template 
void __make_heap(RandomAccessIterator first, RandomAccessIterator last, T*,
	Distance*) {
		if (last - first < 2) return;	
		Distance len = last - first;
		Distance parent = (len - 2)/2; 

		while (true) {
			__adjust_heap(first, parent, len, T(*(first + parent)));
			if (parent == 0) return;	
			parent--;				
		}
}

template 
void __adjust_heap(RandomAccessIterator first, Distance holeIndex,
	Distance len, T value) {
		Distance topIndex = holeIndex;
		Distance secondChild = 2 * holeIndex + 2;	
		while (secondChild < len) {
			if (*(first + secondChild) < *(first + (secondChild - 1)))
				secondChild--;   
			
			*(first + holeIndex) = *(first + secondChild);  
			holeIndex = secondChild;
			secondChild = 2 * (secondChild + 1);
		}
		if (secondChild == len) { 
			*(first + holeIndex) = *(first + (secondChild - 1));
			holeIndex = secondChild - 1;
		}
		__push_heap(first, holeIndex, topIndex, value);
}

template 
void __push_heap(RandomAccessIterator first, Distance holeIndex,
	Distance topIndex, T value) {
		Distance parent = (holeIndex - 1) / 2;	
		while (holeIndex > topIndex && *(first + parent) < value) {
			*(first + holeIndex) = *(first + parent);	
			holeIndex = parent; 
			parent = (holeIndex - 1) / 2;	
		}  
		*(first + holeIndex) = value;	
}

template 
inline void pop_heap(RandomAccessIterator first, RandomAccessIterator last) {
	__pop_heap_aux(first, last, value_type(first));
}

template 
inline void __pop_heap_aux(RandomAccessIterator first,
	RandomAccessIterator last, T*) {
		__pop_heap(first, last-1, last-1, T(*(last-1)), distance_type(first));
}

template 
inline void __pop_heap(RandomAccessIterator first, RandomAccessIterator last,
	RandomAccessIterator result, T value, Distance*) {
		*result = *first;
		__adjust_heap(first, Distance(0), Distance(last - first), value);
}