哈夫曼编码测试
测试要求
设有字符集:S={a,b,c,d,e,f,g,h,i,j,k,l,m,n.o.p.q,r,s,t,u,v,w,x,y,z}。
给定一个包含26个英文字母的文件,统计每个字符出现的概率,根据计算的概率构造一颗哈夫曼树。
并完成对英文文件的编码和解码。
要求:
(1)准备一个包含26个英文字母的英文文件(可以不包含标点符号等),统计各个字符的概率
(2)构造哈夫曼树
(3)对英文文件进行编码,输出一个编码后的文件
(4)对编码文件进行解码,输出一个解码后的文件
(5)撰写博客记录实验的设计和实现过程,并将源代码传到码云
(6)把实验结果截图上传到云班课
测试完成过程
读取文件:
- 对于读取文件,之前是经过了简单的学习,但是还有很多的知识没有掌握。统计字符的时候,学习了一下,采用了下面的写法
//读取文件中出现的字符,并记录出现次数
File file = new File("C:\\Users\\12257\\IdeaProjects\\20172310qx\\src\\Huffman\\text");
if (!file.exists()) {
throw new Exception("文件不存在");
}
BufferedReader fin = new BufferedReader(new FileReader(file));
String line;
//map储存数据的形式是一个key和一个value对应
Map counter = new HashMap();
int total=0;
//读取一个文本行
while ((line = fin.readLine()) != null)
{
int len = line.length();
for (int i = 0; i < len; i++)
{
char c = line.charAt(i);
if (( (c >= 'a' && c <= 'z'&& c == ' ')))
{
continue;
}
// 如果此映射包含指定键的映射关系,则返回 true
if (counter.containsKey(c))
{
counter.put(c, counter.get(c) + 1);
}
else
{
counter.put(c, 1);
}
}
}
fin.close();//文件读取结束
//通过Map.keySet遍历key和value:
Iterator pl = counter.keySet().iterator();
int a = 0;
while (pl.hasNext())
{
char key = pl.next();
int count = counter.get(key);
// System.out.println(key + " --- " + count);
a++;
} 构造哈夫曼树
- 哈夫曼树被称为最优树,有着二叉树的所有性质,但是要带上权重和记住左边的编码为“0”,右边的编码为“1”,所以重写了哈弗曼树的节点类
private T data;//数据
public T getData() {
return data;
}
public void setData(T data) {
this.data = data;
}
protected double weight;//权重
protected Node leftChild;
protected Node rightChild;
public String codeNumber;
public Node(T data , double weight)
{
this.data = data;
this.weight = weight;
this.codeNumber = "";
}
public String getCodeNumber() {
return codeNumber;
}
public void setCodeNumber(String codeNumber) {
this.codeNumber = codeNumber;
}
public double getWeight() {
return weight;
}
public void setWeight(double weight) {
this.weight = weight;
}
public String toString()
{
return "Node[data=" + data
+ ", weight=" + weight + ",codeNumber = "+codeNumber+"]";
}
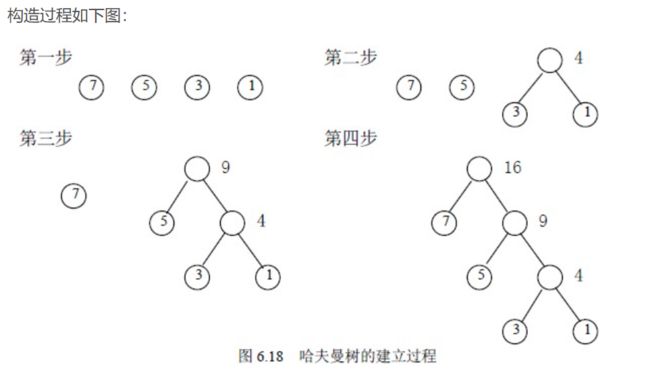
} - 基本思路:1)现在给定的n个有权值的元素,要构成一棵哈弗曼树,首先将这些元素按照权值,从小到大排序
2)然后在其中选择两个权值最小元素构成一棵二叉树的左右孩子,计算两个元素的权值之和,放入该二叉树的根节点中,
3)再从原对列中删除被选中的那两个元素,并且把构成的新的元素加到对列中,重新排序
4)重复2 ,3 操作,直到构成一棵完整的二叉树,就是哈夫曼树。
如图:
public static Node createTree(List nodes) {
// 只要nodes数组中还有2个以上的节点
while (nodes.size() > 1)
{
quickSort(nodes);
//获取权值最小的两个节点
Node left = nodes.get(nodes.size()-1);
left.setCodeNumber(0+"");
Node right = nodes.get(nodes.size()-2);
right.setCodeNumber(1+"");
//生成新节点,新节点的权值为两个子节点的权值之和
Node parent = new Node(null, left.weight + right.weight);
//让新节点作为两个权值最小节点的父节点
parent.leftChild = left;
parent.rightChild = right;
//删除权值最小的两个节点
nodes.remove(nodes.size()-1);
nodes.remove(nodes.size()-1);
//将新节点加入到集合中
nodes.add(parent);
}
return nodes.get(0);
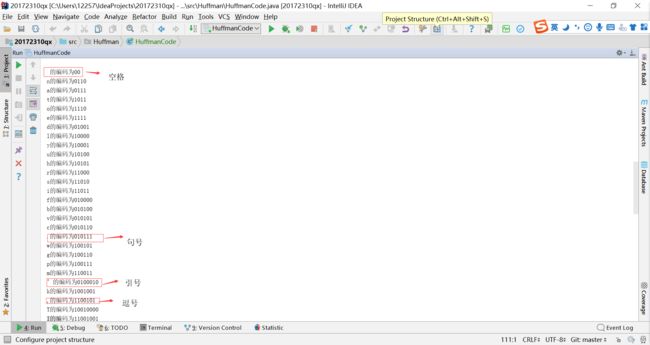
} 编码和解码过程
现在已经对每个字符都进行了对应的编码,只要一一对应就可以相应的编码解码。
double num2 = 0;
for (int i = 0; i < list2.size(); i++) {
num2 += list2.get(i).getWeight();
}
for (int i = 0; i < list3.size(); i++) {
System.out.println("字符为:"+list3.get(i) + "概率为:" + list2.get(i).getWeight() / num2 + " ");
}
System.out.println();
String temp2 = "", temp3 = "";
for (int i = 0; i < list4.size(); i++)
{
System.out.println(list3.get(i) + "的编码为" + list4.get(i) + " ");
}
System.out.println();
List list5 = new ArrayList();
System.out.println();
for (int i = 0; i < result.length(); i++)
{
for (int j = 0; j < list3.size(); j++)
{
if (result.charAt(i) == list3.get(j).charAt(0))
result1 += list4.get(j);
}
}
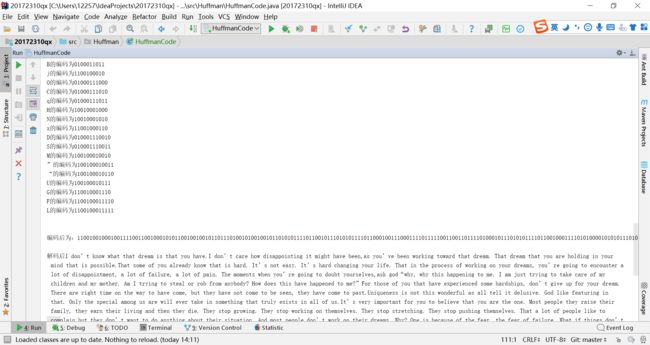
System.out.println("编码后为:" + result1);