随机森林·adaboost·逻辑回归·stacking等方法实现（以titanic数据集为例）【知识整理】

综述

前言

整理一些关于数据分析的知识：本章以titanic数据集的分析为主体，使用python3.6实现集成算法。分析过程包括数据的预处理，数据基础分析及模型应用部分。涉及的代码将分块插入对应部分。（文本内容为作者学习一些数据分析知识之后，自己做的总结。分析上可能会存在争议，但文本中给出的模型的源码及一些基本操作应该是准确的）

摘要

泰坦尼克沉船事件中是否获救是典型的二分类问题。为了预测乘客的获救情况，本文使用了基于逻辑回归（Logistic Regressive）和Adaboost算法的集成模型训练并预测给出的相关数据集。

数据预处理

数据选择

一般情况下，数据集中的所有特征不可能都有统计价值。针对不同的预测目标，有用的特征也会有所不同，此外，根据已有特征我们还可以得出新的有用特征。整个数据集一共提供给我们11个特征，其中船员姓名，船员票号，船舱号等我们认为是无用特征。此外，乘客同行的兄弟姐妹、父母孩子可以整合成为一个同行人数变量，还有乘客名称中有包含乘客称呼的词语，可能可以组成一个新的变量表示为乘客身份等级。

数据缺失处理

数据缺失在该数据库中主要为某个字段信息的缺失，从而造成分析结果的不准确性，使得数据挖掘模型所呈现的不确定性加著，难以把握模型中所蕴含的规律，导致输出的不可靠性。数据库中共有891条记录，可以清晰地道缺失值的属性的个数以及每个属性的未缺失值、缺失值、缺失率等，我们发现只有714名乘客有年龄信息，2名乘客缺少登船口信信息。
以下代码为显示特征的基本属性：

import pandas as pd
import numpy as np
import seaborn as sns

titanic = pd.read_csv('titanic_train.csv')
columns = titanic.columns
print(titanic.describe()) #基础数据显示
#titanic.describe().to_csv('aabbcc.csv')

运行结果：

       PassengerId    Survived      Pclass  ...       SibSp       Parch        Fare
count   891.000000  891.000000  891.000000  ...  891.000000  891.000000  891.000000
mean    446.000000    0.383838    2.308642  ...    0.523008    0.381594   32.204208
std     257.353842    0.486592    0.836071  ...    1.102743    0.806057   49.693429
min       1.000000    0.000000    1.000000  ...    0.000000    0.000000    0.000000
25%     223.500000    0.000000    2.000000  ...    0.000000    0.000000    7.910400
50%     446.000000    0.000000    3.000000  ...    0.000000    0.000000   14.454200
75%     668.500000    1.000000    3.000000  ...    1.000000    0.000000   31.000000
max     891.000000    1.000000    3.000000  ...    8.000000    6.000000  512.329200

通过上述操作我们可以发现缺失的数据。除了缺失数据之外，还会存在一些特征的值是字符类型的离散值。通常这种情况下我们需要对离散值进行转化，所以我们要做以下几个操作：

• Age特征填充： 由于连续变量一般服从高斯分布，所以我们选择了现有样本数据集中年龄的中位数，作为缺失数据年龄特征的值。
• Embarked特征填充： 等船口一共缺失了 2 个，相比于整个数据集缺失的数据较少，我们选择用登船人数最多的口作为缺失数据的值。
• Sex转化： 0 表示male；1 表示female。
• Embarked转化：0 表示 S；1 表示 C；2 表示 Q。

具体代码如下：

"""
预处理:
1、重要特征，填充缺失项
2、字符项用数字转换
"""
titanic['Age'] = titanic['Age'].fillna(titanic['Age'].median()) #中位数填充
print(titanic['Age'].describe())

"""
打印内容为离散的特征
"""
columns = titanic.columns
for i in columns:
    if len(titanic[i].unique()) > 5 or type(titanic[i].unique()[1]) is not str:
        continue
    print(i,titanic[i].unique())

titanic.loc[titanic['Sex']=='male','Sex'] = 0
titanic.loc[titanic['Sex']=='female','Sex'] = 1

titanic['Embarked'] = titanic['Embarked'].fillna('S') #频数最高的值填充
titanic.loc[titanic['Embarked'] == 'S','Embarked'] = 0
titanic.loc[titanic['Embarked'] == 'C','Embarked'] = 1
titanic.loc[titanic['Embarked'] == 'Q','Embarked'] = 2

数据规约

一般我们得到的数据集都回存在同一属性的信息重复出现多次的情况，比如在本文使用的数据集中我们添加的乘客身份信息模块就存在这个问题。经过python软件关键词提取功能，我们得到的数据集中所有代表身份的称呼：Mr，Miss，Mrs，Master，Dr，Rev，Major，Col，Mlle，Mme，Don，Lady，Countess，Jonkheer，Sir，Capt，Ms，Dona
提取的关键词中像Major，Col及Sir，Don都是同一类人的不同称呼，此外Jonkheer，Lady，Countess等应该是属于一类等级的称呼。所以我们对数据进行规定：{“Mr”: 1, “Miss”: 2, “Mrs”: 3, “Master”: 4, “Dr”: 5, “Rev”: 6, “Major”: 7, “Col”: 7, “Mlle”: 8, “Mme”: 8, “Don”: 9, “Lady”: 10, “Countess”: 10, “Jonkheer”: 10, “Sir”: 9, “Capt”: 7, “Ms”: 2, “Dona”: 10}
具体实现方式如下：

import re

# 身份信息提取
def get_title(name):
    title_search = re.search('([A-Za-z]+)\.',name)
    if title_search:
        return title_search.group(1)
    return ""
print(titanic_test['Name'])
titles = titanic['Name'].apply(get_title)
titles2 = titanic_test['Name'].apply(get_title)

#设定精简方式
def tit(titles):
    title_mapping = {"Mr": 1, "Miss": 2, "Mrs": 3, "Master": 4, "Dr": 5, "Rev": 6, "Major": 7, "Col": 7, "Mlle": 8, "Mme": 8, "Don": 9, "Lady": 10, "Countess": 10, "Jonkheer": 10, "Sir": 9, "Capt": 7, "Ms": 2, "Dona": 10}
    for k,v in title_mapping.items():
        titles[titles == k] = v
    return titles

titanic['Title'] = tit(titles)
titanic_test['Title'] = tit(titles2)

此外，我们还能从以后的特征中提取其他特征，例如同行成员，用户名称长度等。具体代码如下：

#   同行数量
titanic['FamilySize'] = titanic['SibSp']+titanic['Parch']
titanic_test['FamilySize'] = titanic_test['SibSp']+titanic_test['Parch']
#   名字长度
titanic['NameLength'] = titanic['Name'].apply(lambda  x:len(x)) #名字长度
titanic_test['NameLength'] = titanic_test['Name'].apply(lambda  x:len(x)) #名字长度

一些简单模型的实现

线性回归实现

# 线性回归（交叉验证）
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import KFold

# 说明特征
predictors = ['Pclass','Sex','Age','SibSp','Parch','Fare','Embarked']

# 调入线性回归模型
alg = LinearRegression()

# 规定交叉验证拆分的个数，随机种子的值
kf = KFold(n_splits=3, shuffle= False)
predications = []
for train,test in kf.split(titanic):
    train_predictors = titanic[predictors].iloc[train,:]
    train_target = titanic['Survived'].iloc[train]
    alg.fit(train_predictors,train_target)
    test_predicatiors = titanic[predictors].iloc[test,:]
    test_predications = alg.predict(test_predicatiors)
    predications.append(test_predications)

predications = np.concatenate(predications,axis=0)

predications[predications >.5] = 1
predications[predications <=.5] = 0
accuracy = len(predications[predications == titanic["Survived"]]) / len(predications)
print(accuracy) #准确率
# 0.7833894500561167

随机森林方法实现

使用未添加新特征前的数据

# 调入测试集
titanic_test = pd.read_csv('titanic_test.csv')
titanic_test['Age'] = titanic_test['Age'].fillna(titanic_test['Age'].median())
titanic_test['Fare'] = titanic_test['Fare'].fillna(titanic_test['Fare'].median())
titanic_test.loc[titanic_test['Sex'] == 'male','Sex'] = 0
titanic_test.loc[titanic_test['Sex'] == 'female','Sex'] = 1
titanic_test['Embarked'] = titanic_test['Embarked'].fillna('S')

titanic_test.loc[titanic_test['Embarked'] == 'S','Embarked'] = 0
titanic_test.loc[titanic_test['Embarked'] == 'C','Embarked'] = 1
titanic_test.loc[titanic_test['Embarked'] == 'Q','Embarked'] = 2

#随机森林
#from sklearn import cross_validation 被下面调用方式取代
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifier

alg = RandomForestClassifier(random_state= 1, n_estimators=10,min_samples_split=2,min_samples_leaf=1)
kf= KFold(n_splits=3,random_state=1)
scores = cross_val_score(alg,titanic[predictors],titanic['Survived'],cv = kf)
print(scores.mean())
#0.7856341189674523 效果并不是非常好

调整后随机森林各项指标后：

# 此时我们要对模型进行调整
alg = RandomForestClassifier(random_state= 1, n_estimators=50,min_samples_split=4,min_samples_leaf=2)
kf= KFold(n_splits=3,random_state=1)
scores = cross_val_score(alg,titanic[predictors],titanic['Survived'],cv = kf)
print(scores.mean())
#0.8159371492704826 结果变好了,此时分类器内部提升会很有限，我们回到输入值选择

通过调整前后的结果差异可以看出，增加随机森林中的分类器数量等参数可以提升准确性。
但是这样的提升只局限于参数的改变，提升的效果微乎其微。

使用添加新特征后的数据

predictors = ['Pclass','Sex','Age','SibSp','Parch','Fare','Embarked','FamilySize','Title','NameLength']

alg = RandomForestClassifier(random_state= 1, n_estimators=50,min_samples_split=4,min_samples_leaf=2)
kf= KFold(n_splits=3,random_state=1)
scores = cross_val_score(alg,titanic[predictors],titanic['Survived'],cv = kf)
print(scores.mean())
#0.8350168350168351

增加变量后得出的结果提升了。

数据分析

特征重要性的选取

from sklearn.feature_selection import SelectKBest,f_classif
import matplotlib.pyplot as plt
# 特征重要性
predictors = ['Pclass','Sex','Age','SibSp','Parch','Fare','Embarked','FamilySize','Title','NameLength']

selector = SelectKBest(f_classif,k=5)
selector.fit(titanic[predictors],titanic['Survived'])

scores = -np.log10(selector.pvalues_)

plt.bar(range(len(predictors)),scores)
plt.xticks(range(len(predictors)),predictors,rotation = 'vertical')
plt.show()

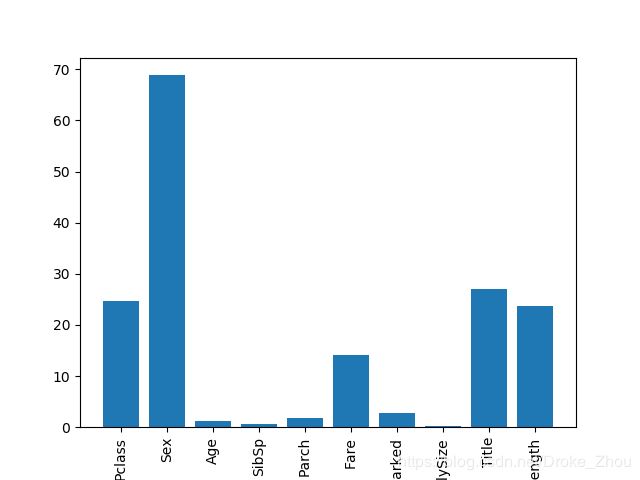
经过数据处理后，我们得到了一份较为完整得数据集，在运用模型之前我们要对数据进行简单分析。主要分析分为两大部分：第一部分为几个变量同获救之间的相关性分析；第二部分为多个变量之间的相关性分析。

结果与变量的分析

• 在绘图之前我们要导入数据集

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_style("whitegrid")
# 数据读取部分
data = pd.read_csv("titanic_data.csv")
print(data.head())
survived_a = pd.read_csv("AA.csv")
survived_b = pd.read_csv("AB.csv")
survived_c = pd.read_csv("AC.csv")
survived_d = pd.read_csv("titanic_survived.csv")
survived = pd.DataFrame()
survived['Adaboost'] = survived_a['0']
survived['LR'] = survived_b['0']
survived['ST'] = survived_c['0']
survived['really'] = survived_d['Survived']
print(survived.head())

• 获救与未获救

# 研究各项指标与获救情况的关系
sns.set_style("whitegrid")
# 生存情况
new_data = data
new_data['values'] = data['PassengerId']/data['PassengerId']
new_data['values'] = new_data['values'].astype(int)
new_data.loc[new_data['Survived'] == 0,'vv'] = sum(new_data.loc[new_data['Survived']==0,'values'])
new_data.loc[new_data['Survived'] == 1,'vv'] = sum(new_data.loc[new_data['Survived']==1,'values'])
new_data.loc[new_data['Survived'] == 0,'Survived'] = 'noSurvived'
new_data.loc[new_data['Survived'] == 1,'Survived'] = 'Survived'
sns.barplot(data=new_data,x = 'Survived',y='vv',color="#0089A7",alpha = 0.7)
plt.ylabel('number of survived')
plt.show()

从训练集样本中获救的情况来看，未获救人数大于获救人数，两者之间的样本比例较均衡未出现较大偏差。然后，为了探究变量与是否获救之间的关系，我们选择了性别、登船口、年龄等几个变量进行分析。

• 绘图代码：

new_data.loc[new_data['Sex'] == 0,'Sex'] = 'male'
new_data.loc[new_data['Sex'] == 1,'Sex'] = 'female'
sns.violinplot(x = 'Survived', y = 'Age', hue = 'Sex',data = new_data,split = True,palette=["#a5dee4","#eb7a77"])
plt.show()
new_data.loc[new_data['Embarked'] == 0,'Embarked'] = 'S'
new_data.loc[new_data['Embarked'] == 1,'Embarked'] = 'C'
new_data.loc[new_data['Embarked'] == 2,'Embarked'] = 'Q'
sns.violinplot(x = 'Pclass', y = 'Age', hue = 'Survived',data = new_data,split = True,palette=["#fb9966","#66bab7"])
plt.show()
#其中有一张图的代码可以通过修改上述代码实现

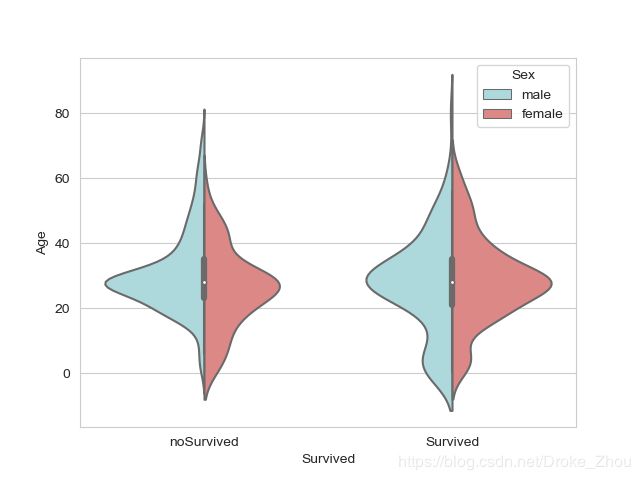
从图上结果来看，船上乘客多以20 - 40岁的青年为主。从获救情况来看女性的获救可能性大于男性，且获救的人大部分为20 - 40岁的青年人群复合高斯分布结果。从登船口来看，S口与C口的船员数量最多；但从逃生情况来看，Q口的逃生人数要比未逃生人数多。此外从票价及船票等级来看，一等票的购票人数年龄大于所有船员均值，且他们的逃生人数比未逃生人数多，二等票及三等票的儿童逃生人数较多。

变量间的相关性分析

• 代码包括相关性矩阵及绘图

data_need = titanic[predictors]
data_need = data_need.corr()
# 温度图
plt.figure()
ax = sns.heatmap(data_need,annot = True,fmt='.2f',cmap = 'YlGnBu',linewidths=.5)
plt.show()

# hue分类图
predictors=['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Fare', 'Embarked', 'FamilySize', 'Title', 'NameLength','Survived']
G = titanic[predictors]
G = G.sort_values('Survived')
G = pd.DataFrame(G)
g = sns.pairplot(pd.read_csv('titanic_data.csv'),vars=['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Fare', 'Embarked', 'FamilySize', 'Title', 'NameLength'],kind='reg',size=2.5)
plt.show()

# 添加reg图
g = sns.PairGrid(pd.read_csv('titanic_data.csv'),vars=['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Fare', 'Embarked', 'FamilySize', 'Title', 'NameLength'],hue='Survived',palette=['r','#58B2DC'])
g.map_diag(plt.hist,edgecolor = 'black',alpha = 1)#对角线上图片
g.map_offdiag(plt.scatter,s = 3,alpha = 0.5 )#非对角线上图片
g.add_legend()
plt.show()

data_need.to_csv("corr.csv",index=True,header=True)

运行结果：

              Pclass       Sex       Age  ...  Embarked  FamilySize  NameLength
Pclass      1.000000 -0.131900 -0.339898  ...  0.045702    0.065997   -0.220001
Sex        -0.131900  1.000000 -0.081163  ...  0.116569    0.200988    0.448759
Age        -0.339898 -0.081163  1.000000  ... -0.009165   -0.245619    0.039702
SibSp       0.083081  0.114631 -0.233296  ... -0.059961    0.890712    0.165019
Parch       0.018443  0.245489 -0.172482  ... -0.078665    0.783111    0.252282
Fare       -0.549500  0.182333  0.096688  ...  0.062142    0.217138    0.155832
Embarked    0.045702  0.116569 -0.009165  ...  1.000000   -0.080281   -0.107749
FamilySize  0.065997  0.200988 -0.245619  ... -0.080281    1.000000    0.238820
NameLength -0.220001  0.448759  0.039702  ... -0.107749    0.238820    1.000000

我们一般定义数值的绝对值在0.8和1.0之间为极强相关，0.6和0.8之间为强相关，0.4和0.6之间为中等程度相关，0.2和0.4之间为弱相关，0.0和0.2之间为极弱相关或无相关。忽视Sibsp和FamilySize，Pclass和Fare等相似因子之间的相关性，我们可以看出和Pclass相关性最高的为Age，却仅为负弱相关。和Sex相关性最高的为Parch，为负弱相关。和Sibsp相关性较高的为Parch，为正中等程度相关。与Parch相关性最高的为Familysize，有0.89的正极强相关。除了个别变量之间存在极强相关性和中等程度相关，其余变量之间均为弱相关或极弱相关。

模型介绍

逻辑回归

在之前的有做过具体的介绍不再赘述推导过程。
船员获救情况属于典型的二分类问题。逻辑回归(Logistic Regressive)显然是一个比较好的训练模型。针对泰坦尼克数据，本文建立了回归函数：
$$LR(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_1{x}_1+...++{\theta }_9{x}_9=\sum _{i=1}^9{\theta }_i{x}_i={\theta }^{T}x$$

再完成逻辑回归(Logistic Regressive)时，我们以Sigmoid函数作为核心，建立了模型的预测函数：
$$h_{\theta }(x)=g({\theta }^{T}x)=\frac{1}{1+e^{-{\theta }^{T}x}}$$
一般预测函数得出的结果都为$0$到$1$区间上的一个值，为了实现二分类，本文设置了如下分类方式：
$$P(y=1|x;\theta )=(h_{\theta }(x){)}^y(1-h_{\theta }(x){)}^{1-y}$$

再使用似然函数取对数，梯度下降法得到代价函数的方式实现逻辑回归。具体的实现方式：本文调用python软件中sklearn库直接对数据集进行分析。

Adaboost

为了提升模型预测的准确性，我们还采用了随机森林方法，对于给定的泰坦尼克训练集数据，我们采用Adaboost算法。Adaboost是一种迭代算法，其核心思想是针对同一个训练集训练不同的分类器(弱分类器)，然后把这些弱分类器集合起来，构成一个更强的最终分类器(强分类器)。其算法本身是通过改变数据分布来实现的，它根据每次训练集之中每个样本的分类是否正确，以及上次的总体分类的准确率，来确定每个样本的权值。将修改过权值的新数据集送给下层分类器进行训练，最后将每次训练得到的分类器最后融合起来，作为最后的决策分类器。使用Adaboost分类器可以排除一些不必要的训练数据特征，并放在关键的训练数据上面。

该算法的大致思想为：训练数据的每一个样本，并赋予其一个权重，这些权值构成权重向量$D$，维度等于数据集样本个数。开始时，这些权重都是相等的，首先在训练数据集上训练出一个弱分类器并计算该分类器的错误率，然后在同一数据集上再次训练弱分类器，但是在第二次训练时，将会根据分类器的错误率，对数据集中样本的各个权重进行调整，分类正确的样本的权重降低，而分类错的样本权重则上升，但这些权重的总和保持不变为$1$。

并且，最终的分类器会基于这些训练的弱分类器的分类错误率，分配不同的决定系数$\alpha$，错误率低的分类器获得更高的决定系数，从而在对数据进行预测时起关键作用。$\alpha$的计算根据错误率得来：
$$\alpha =0.5\times ln(1-\frac{\epsilon }{max(\epsilon ,10^{-16})})$$

其中，$\epsilon =$为正确分类的样本数目/样本总数，$max(\epsilon ,10^{-16})$是为了防止错误率为而造成分母为$0$的情况发生。

计算出$\alpha$之后，就可以对权重向量进行更新了，使得分类错误的样本获得更高的权重，而分类正确的样本获得更低的权重。$D$的计算公式如下：

如果某个样本被正确分类，那么权重更新为：
$$D(m+1,i)=D(m,i)\times \frac{e^{-\alpha }}{sum(D)}$$

如果某个样本被错误分类，那么权重更新为：
$$D(m+1,i)=D(m,i)\times \frac{e^{\alpha }}{sum(D)}$$

其中，$m$为迭代的次数，即训练的第$m$个分类器，$i$为权重向量的第$i$个分量，$i\le$数据集样本数量。

当我们更新完各个样本的权重之后，就可以进行下一次的迭代训练。AdaBoost算法会不断重复训练和调整权重，直至达到迭代次数，或者训练错误率为$0$。

算法融合

我们采用stacking模型思想，对Adaboost算法和逻辑回归算法进行融合。

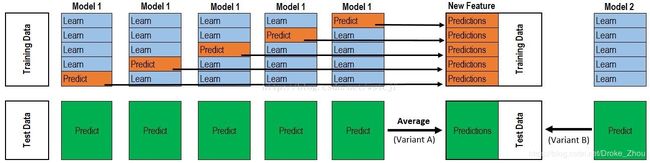
大致思路为，我们对Adaboost，即Model1分5分进行交叉验证。每一次的交叉验证包含两个过程，1. 基于training data训练模型；2. 基于training data训练生成的模型对testing data进行预测。在整个第一次的交叉验证完成之后我们将会得到关于当前testing data的预测值，遍历所有的测试集，我们就能得到所有的预测值，Model2表示为逻辑回归，直接对数据集预测能得到预测值。

两次模型预测可以得到两组泰坦尼克逃生预测值，本文再采用线性回归的方式对两种模型的预测值加权得到最终的预测结果。最终的预测结果，即我们得出的最终逃生预测值。

指标评估

评估体系主要采用如下几个方面。

召回率(Recall)

召回率(Recall)是检索出的相关文档数和文档库中所有的相关文档数的比率，衡量的是检索系统的查全率。

$$R=\frac{TP}{(TP+FN)}$$

准确率(Accuracy)

准确率(Accuracy)是正确检索出的有关无关文档数和文档库中全部文档数的百分比。

$$A=\frac{TP+TN}{(TP+FP+FN+TN)}$$

我们将采用以上两种指标，衡量我们模型预测结果的优劣。

阈值选取的指标

为了最优选取最佳阈值，我们引入了阈值评价体系，即采用准确率和召回率的加权平均数作为衡量某种阈值条件下模型的性能：
$$P=\frac{A+R}{2}$$
　　
当性能达到最优值时，我们认为此时的阈值是最优的。

代码实现模块

算法具体由python3.6实现，调用库有sklearn、pandas等。我们先将处理好的训练集数据投入到逻辑回归(Logistic Regressive)模型及Adaboost模型中，得出一个初步的获救率，再将两个模型得出的求生率投入到集成模型中即可完成模型训练。

根据训练好的模型我们可以测试得到的训练集的结果，以及测试集的结果。需要注意的是，我们通过模型得到的是每个样本预测的获救率，为进一步确定船员是否获救，我们需要对阈值进行研究。

模型经过原始训练数据集和测试集得到的每个乘客能够获救的概率P，我们需要设置一个阈值$\delta$，当P>$\delta$，判断该乘客能够获救；反之，则判断该乘客无法获救。同时实验来选取阈值$\delta$。为了能找出最佳阈值，我们采用了离散化方式，将可行的阈值划分为20类。用阈值评估模型中的性能代表阈值的优劣，对所有阈值进行遍历。结果如下图。

• 代码模块：

# 阈值最优图像
line = np.arange(0,1,0.05)
need = pd.DataFrame(np.zeros((len(line),3)),columns=['Adaboost','LR','ST'])
for i in line:
    new_s=survived[['Adaboost','LR','ST']]
    values = pd.DataFrame(survived['really'].values,columns=['a'])
    new_s[new_s < i] = 0
    new_s[new_s >= i] = 1
    for j in new_s.columns:
        accuracy = len(new_s[new_s[j] == values['a']]) / len(values)
        number = 0
        for t in range(418):
            if new_s.loc[t][j] == values.loc[t,'a'] and new_s.loc[t,j] ==1:
                number +=1
        t = len(new_s[new_s[j]==1])
        if len(new_s[new_s[j]==1]) == 0:
            t = 0.000001
        zhanghai = number / t
        need.loc[i/0.02,j] = (accuracy+zhanghai) / 2
    need.loc[i/0.02,'line'] = round(i,2)

need = need.dropna(axis=0)
need = need.sort_values('line')
# 绘制阈值图像
sns.pointplot(need['line'],need['Adaboost'],color="#a5dee4",alpha = 0.3,s = 1,label = 'Adaboost')
sns.pointplot(need['line'],need['LR'],color="#91b493",alpha = 0.3,s = 1,label = 'LR')
sns.pointplot(need['line'],need['ST'],color="#eb7a77",alpha = 0.3,s = 1,label = 'ST')
plt.xlabel(" threshold value")
plt.ylabel("performance")
plt.show()

由图可以看出，权衡模型性能的表现，我们取0.55作为最优的阈值。由此图同时也可以说明在我们的集成模型取最佳阈值时，模型性能优于Adaboost迭代算法以及逻辑回归模型。

算法实现模块

# 集成算法  LR,Boosting
from sklearn.ensemble import  GradientBoostingClassifier
from sklearn.linear_model import LogisticRegression
import numpy as np

def complex_LR_Boosting(index,value):
    algorithms = [
        [GradientBoostingClassifier(random_state=1,n_estimators=40,max_depth=3),index],
        [LogisticRegression(random_state=1),index]
    ]
    kf = KFold(n_splits=3,random_state=1)
    predications = []
    for train,test in kf.split(titanic):
        train_target = titanic[value].iloc[train]
        full_test_predictions = []
        for alg,predictors in algorithms:
            alg.fit(titanic[predictors].iloc[train,:],train_target)

            test_predications = alg.predict_proba(titanic[predictors].iloc[test,:].astype(float))[:,1]
            full_test_predictions.append(test_predications)
        test_predications = (full_test_predictions[0]+full_test_predictions[1])/2

        dataline = 0.58
        test_predications[test_predications< dataline] = 0
        test_predications[test_predications>=dataline] = 1
        predications.append(test_predications)

    predications = np.concatenate(predications,axis=0)
    accuracy = len(predications[predications == titanic[value]])/len(predications)
    print(accuracy)

index = ['Pclass','Sex','Age','SibSp','Parch','Fare','Embarked','FamilySize','Title']
value = 'Survived'
complex_LR_Boosting(index,value)

alg = GradientBoostingClassifier(random_state=1,n_estimators=40,max_depth=3)
alg.fit(titanic[index],titanic[value])
print(alg)

algorithms = [
    [GradientBoostingClassifier(random_state=1,n_estimators=40,max_depth=3),index],
    [LogisticRegression(random_state=1),index],
    [RandomForestClassifier(random_state= 1, n_estimators=50,min_samples_split=4,min_samples_leaf=2),index]
]
titanic_test['Survived'] = pd.read_csv('titanic_survived.csv')['Survived']
print(titanic_test)
predications = []
full_test_predictions = []
set_index = [0,1,0]
for alg, predictors in algorithms:
    alg.fit(titanic[predictors],titanic[value])
    test_predications = alg.predict_proba(titanic_test[predictors].astype(float))[:,1]
    full_test_predictions.append(test_predications)
test_predications = (full_test_predictions[0]*set_index[0]+full_test_predictions[1]*set_index[1])/sum(set_index)
dataline = 0.5
test_predications[test_predications< dataline] = 0
test_predications[test_predications>=dataline] = 1
predications.append(test_predications)
predications = np.concatenate(predications,axis=0)
accuracy = len(predications[predications == titanic_test[value]])/len(predications)

混淆矩阵绘制

#混淆矩阵（图像表示recall）：精度等于正对角线合/总数
import itertools
from sklearn.metrics import confusion_matrix
def plot_confusion_matrix(cm, classes,
                          title='Confusion matrix',
                          cmap=plt.cm.Blues):
    """
    This function prints and plots the confusion matrix.
    """
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, rotation=0)
    plt.yticks(tick_marks, classes)

    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, cm[i, j],
                 horizontalalignment="center",
                 color="white" if cm[i, j] > thresh else "black")

    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')

cnf_matrix = confusion_matrix(titanic_test[value],predications)
plt.figure()
plot_confusion_matrix(cnf_matrix
                      , classes=[0,1]
                      , title='Confusion matrix')
plt.title('LR')
plt.show()

解释：set_index = [x,x,x]表示每种方法对应的系数（由于最终我们没有使用随机僧林所以最后一个x = 0）。在绘制混淆矩阵时，我们采用定义函数的方式，与模型代码块一起使用即可，注意需要修改title名称。

评估分析

通过代码运行之后的结果我们就能对模型进行评估了。
在模型建立过程中，为了确定最佳方案，我们分别采用Adaboost迭代算法、逻辑回归(Logistic Regressive)模型以及将两种方案结合对乘客进行获救预测分析，最终将测得性能进行了对比。

Adaboost迭代算法结合实际数据得出的混淆矩阵如图2所示，通过运算得出召回率(Recall)最终结果为91.64%，准确率(Accuracy)最终结果为90.91%。

逻辑回归(Logistic Regressive)模型结合实际数据得出的混淆模型如图3所示，通过运算得出召回率(Recall)最终结果为95.09%，准确率(Accuracy)最终结果为93.54%。

我们的模型结合Adaboost迭代算法和逻辑回归(Logistic Regressive)模型，其召回率(Recall)最终结果为96.96%，准确率(Accuracy)最终结果为95.45%，都高于另外两种方案，说明我们的模型具有优异的性能，可以准确预测乘客是否获救，具有较强的泛化性能。

小结

本章以titanic数据分析作为载体，实现了随机森林·adaboost·逻辑回归·stacking等方法。主要需要理解代码块的功能。数据分析上还有待完善，在之后的分析中会进一步详细说明。（stacking流程图、Adaboost原理部分来自网络）