前想映射后向映射的双线性插值算法

转载于：https://blog.csdn.net/glorydream2015/article/details/44873703
公式格式存在问题，大家请移步原博客吧。

一，图像变换与映射
我们在进行图像处理时常常需要对图像进行变换。比如对图像进行缩放，旋转，平移等。图像变换的本质是将像素点的坐标通过某一种函数关系，映射到另外的位置。假设变换前图像为I(x,y)，变换后图像为I’(x’,y’)，则变换前后的图像之间存在下列关系

(x′y′)=(f(x,y)g(x,y))I(x,y)=I′(x′,y′)=I′(f(x,y),g(x,y))(1)

(x′y′) ( x ′ y ′ )

=

(f(x,y)g(x,y)) ( f ( x , y ) g ( x , y ) )

\\ I(x,y)=I'(x',y')=I'(f(x,y),g(x,y)) \tag 1

(xy)=(f−1(x′,y′)g−1(x′,y′))I′(x′,y′)=I(x,y)=I(f−1(x′,y′),g−1(x′,y′))(2)

(xy) ( x y )

=

(f−1(x′,y′)g−1(x′,y′)) ( f − 1 ( x ′ , y ′ ) g − 1 ( x ′ , y ′ ) )

\\ I'(x',y')=I(x,y)=I(f^{-1}(x',y'),g^{-1}(x',y')) \tag 2
公式(1)我们已知原图像到目标图像的坐标变换(f(x,y),g(x,y))，因此我们可以知道原图像的一点在变换后在目标图像的位置，我们称为向前映射。
相反，公式(2)中我们知道目标图像的一点(x’,y’)在变换前在原图像上的位置 (f−1(x′,y′),g−1(x′,y′))，我们称为向后映射。

二、插值：向前映射与向后映射
我们知道，通常情况下，一个整数位置(x,y)经过图像变换后，往往都位于非整数位置。此时就要采用插值技术。此时对于向前映射和向后映射，需要采取不同的策略。

下图为向前映射的示意图。输入图像上整数点坐标映射到输出图像之后，变成了非整数点坐标。因此，需要将其像素值按一定权重分配到其周围四个像素点上。对于输出图像而言，其整数点像素值周围会有很多输入图像像素映射过来，每个到其周围的非整数点像素值都会分配一定的灰度值到它上面，将这些分配而来的像素值叠加，就是输出图像整数点位置的像素值。由于这个分配、叠加的特性，向前映射法有时也叫像素移交映射。

因此，对于向前映射而言，输出图像某一点的像素值不能直接得到，需要遍历输入图像的所有像素值，对其进行坐标变换，分配像素值到整数位置，才能得到输出图像各像素点的像素值。这是向前映射法的缺点。

相比之下，向后映射法就比较直观。在这种情况下，我们知道输出图像上整数点位置(x’,y’)在变换前位于输入图像上的位置(x,y)，一般来说这是个非整数点位置，利用其周围整数点位置的输入图像像素值进行插值，就得到了该点的像素值。我们遍历输出图像，经过坐标变换、插值两步操作，我们就能将其像素值一个个地计算出来，因此向后映射又叫图像填充映射。如下图所示。

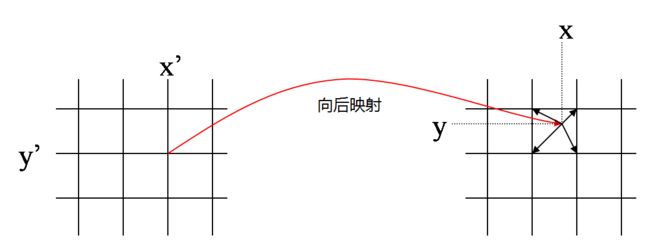
插值算法我们采用双线性插值，如下图所示

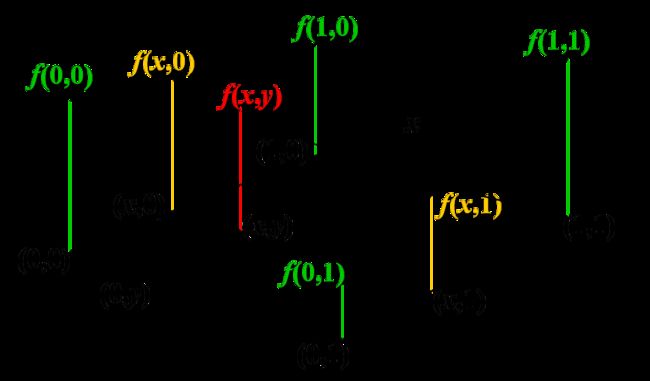
这次我们先看向后插值。这种情况下输出图像上某点的像素值I’(x’,y’)映射到f(x,y),而f(x,y)由输入图像上四点像素值叠加而成

f(x,y)=(1−x)∗(1−y)∗f(0,0)+(1−x)∗y∗f(0,1)+x∗(1−y)∗f(1,0)+x∗y∗f(1,1)

f(x,y)=(1-x)*(1-y)*f(0,0)+(1-x)*y*f(0,1)+x*(1-y)*f(1,0)+x*y*f(1,1)
很容易验证四个权重系数之和为1，插值后图像亮度不变。
对向前插值，输入图像某点I(x,y)变换到输出图像(x’,y’)的位置，因此需要将其像素值分配到f(0,0)，f(0,1)，f(1,0)，f(1,1)四个位置。分配方式为

f(0,0)=(1−x)∗(1−y)∗f(x,y)f(0,1)=(1−x)∗y∗f(x,y)f(1,0)=x∗(1−y)∗f(x,y)f(1,1)=x∗y∗f(x,y)

f(0,0)=(1-x)*(1-y)*f(x,y) \\ f(0,1)=(1-x)*y*f(x,y) \\ f(1,0)=x*(1-y)*f(x,y)\\ f(1,1)=x*y*f(x,y)
对向前映射而言，虽然分配系数之和为1。但输出图像上每个点的像素值是多个分配值叠加而成的，不能保证所有分配到其上的权重之和为1。因此必须记录下所有分配到其上的权重并累加起来，最后利用累加权重进行归一化，才能得到正确的插值结果。

三、结果验证
利用旋转变换来严重上述理论，规定图像从左到右为x轴正方向，从上到下为y轴正方向，原点位于左上角。逆时针旋转为正。则图像的旋转变换公式为

(x′y′)=(α−ββα)(xy)+((1−α)x0−βy0βx0+(1−α)y0)

[Math Processing Error] ( x ′ y ′ ) =

[Math Processing Error] ( α β − β α )

[Math Processing Error] ( x y ) +

[Math Processing Error] ( ( 1 − α ) x 0 − β y 0 β x 0 + ( 1 − α ) y 0 )
其中 α=s∗cos(θ),β=s∗sin(θ),s为缩放系数。
利用上式我们很容易进行向前映射。
要进行向后映射，我们需要将上式稍作变换，改写成以(x’,y’)表示(x,y)的形式。
使用OpenCV进行编程，分别使用向前映射和向后映射方法进行旋转变换，以下为变换结果
原图片

旋转30°，向后映射

旋转30°，向前映射

四、总结
向后映射比较直观，计算量也小，我们经常使用的图像变换都是采用向后映射的方法来处理。但向后映射需要知道变换的反变换公式，在上面旋转变换的情况，反变换很容易求出来。但在有些变换比较复杂的场合，这个反变换是很难得到的。此时就需要采用前向映射的方法进行变换了。从实验结果看，向前映射得到的结果与向后映射是一样的。