cs231 卷积神经网络Convolutional Networks群组归一化GN( Group Normalization)

cs231 Convolutional Networks Group Normalization:

 

 

def spatial_groupnorm_forward(x, gamma, beta, G, gn_param):
    """
    Computes the forward pass for spatial group normalization.
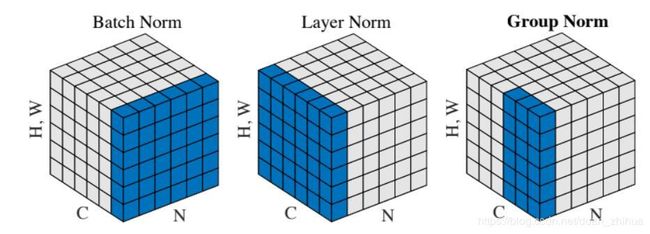
    In contrast to layer normalization, group normalization splits each entry 
    in the data into G contiguous pieces, which it then normalizes independently.
    Per feature shifting and scaling are then applied to the data, in a manner identical to that of batch normalization and layer normalization.

    Inputs:
    - x: Input data of shape (N, C, H, W)
    - gamma: Scale parameter, of shape (C,)
    - beta: Shift parameter, of shape (C,)
    - G: Integer mumber of groups to split into, should be a divisor of C
    - gn_param: Dictionary with the following keys:
      - eps: Constant for numeric stability

    Returns a tuple of:
    - out: Output data, of shape (N, C, H, W)
    - cache: Values needed for the backward pass
    """
    out, cache = None, None
    eps = gn_param.get('eps',1e-5)
    ###########################################################################
    # TODO: Implement the forward pass for spatial group normalization.       #
    # This will be extremely similar to the layer norm implementation.        #
    # In particular, think about how you could transform the matrix so that   #
    # the bulk of the code is similar to both train-time batch normalization  #
    # and layer normalization!                                                # 
    ###########################################################################
    #pass
    N, C, H, W = x.shape
    # 按分组g将大的立方体积木拆成 C/G个小积木体。
    #N, C, H, W = 2, 6, 4, 5;G = 2 ;这里g为2个一组，拆成6/2=3组小立方体。
    x = x.reshape((N * G, C // G * H * W)) #(N, C, H, W)--->(N * G, C // G * H * W) 
    #接下来就可以将每1个小立方体作为一个Layer Norm的模块去处理。     
    x = x.T #(C // G * H * W,N * G)
    mean_x = np.mean(x,axis =0)
    var_x= np.var(x,axis = 0)
    inv_var_x = 1 / np.sqrt(var_x + eps)
    
    x_hat = (x - mean_x)/np.sqrt(var_x + eps) ##(C // G * H * W,N * G)
    x_hat = x_hat.T #(C // G * H * W,N * G)---->(N * G, C // G * H * W)
    
    
    x_hat = x_hat.reshape((N, C, H, W)) #(N * G, C // G * H * W)---->(N, C, H, W)
   

    
    out = gamma * x_hat + beta  
    cache =( x_hat,gamma,mean_x,inv_var_x, G)

    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return out, cache


def spatial_groupnorm_backward(dout, cache):
    """
    Computes the backward pass for spatial group normalization.

    Inputs:
    - dout: Upstream derivatives, of shape (N, C, H, W)
    - cache: Values from the forward pass

    Returns a tuple of:
    - dx: Gradient with respect to inputs, of shape (N, C, H, W)
    - dgamma: Gradient with respect to scale parameter, of shape (C,)
    - dbeta: Gradient with respect to shift parameter, of shape (C,)
    """
    dx, dgamma, dbeta = None, None, None

    ###########################################################################
    # TODO: Implement the backward pass for spatial group normalization.      #
    # This will be extremely similar to the layer norm implementation.        #
    ###########################################################################
    pass

    x_hat,gamma,mean_x,inv_var_x, G = cache 
   
    #x_hat :(N, C, H, W)
    N, C, H, W = x_hat.shape
    # 在(N, H, W)维度上计算
    dgamma = np.sum(dout * x_hat, axis=(0, 2, 3), keepdims=True)
    dbeta = np.sum(dout, axis=(0, 2, 3), keepdims=True)
    #forward时拆分成几个小立方体积来计算的，backward反向传播时仍需分组拆成几个小立方体计算。
   
    #dout :(N, C, H, W)--->(N * G, C // G * H * W) ---->(C // G * H * W, N * G)   
    dxhat = (dout * gamma).reshape((N * G, C // G * H * W)).T 
    
    #x_hat:(N, C, H, W)--->(N * G, C // G * H * W) ---->(C // G * H * W, N * G)
    x_hat = x_hat.reshape((N * G, C // G * H * W)).T    
    
    # d:   C // G * H * W 将每1个小立方体作为一个Layer Norm的反向backward模块去处理
    d = x_hat.shape[0]
    dx = (1. / d) * inv_var_x * (d * dxhat - np.sum(dxhat, axis=0) -
                                 x_hat * np.sum(dxhat * x_hat, axis=0))    
    
    
    dx = dx.T #(C // G * H * W, N * G) ----->(N * G, C // G * H * W) 
    # 将几个小立方体再重新拼接成一个大立方体
    dx = dx.reshape((N, C, H, W)) #(N * G, C // G * H * W) --->(N, C, H, W)
    
   

    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return dx, dgamma, dbeta

 

https://github.com/duanzhihua