模型集成（Ensemble）

1. 模型集成的框架

  模型集成的框架是这样的，有很多种分类器，它们应该是不同的，可以是不同的机器学习方法，也可以是相同的方法。但是它们最好是互补的，也就是说不是互相相似的。每种分类器都应该有自己的位置。

2. Ensemble：Bagging

  在本节中会以某一种机器学习方法举例，但是实际上这种集成方法适用于任何的机器学习方法。

2.1 回顾偏置与方差的关系

  偏置与方差的关系如下图所示

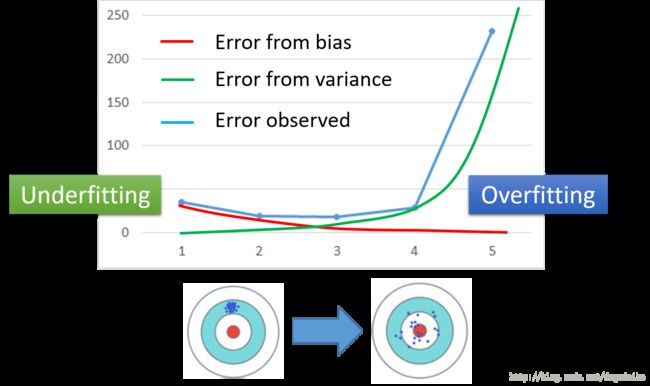
除了可以很完美进行工作的机器学习模型，剩下的模型大致可以分为两种情况，即欠拟合（Underfitting）和过拟合（Overfitting）。欠拟合的特点在于它具有比较小的方差，但是却有着比较大的偏置（即与正确答案的偏离方向）；而过拟合虽然有着较小的偏置，但是却有着较大的方差，将这两种情况画在一起如上图所示，随着模型复杂程度的增大，模型的效果会先提高后降低。

2.2 Bagging的方法

  Bagging的方法如下图所示

他利用可放回抽样总共获得N个样本，之后训练N个分类器，对于回归问题取这N个分类器的均值，对于分类问题让这N个分类器进行投票，

  主要注意的是，这种方法主要用在抑制模型过拟合的问题，比如说决策树。这种方法在NN上用的并不多，因为NN实际上没有想象中那么容易过拟合，它往往是在训练集上不能获得100% 的正确率的。

  下面是一个使用决策树进行分类的例子

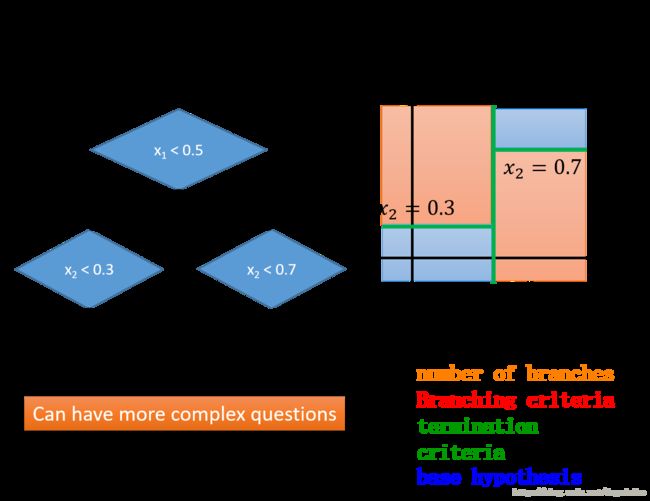
将决策树化成图形的形式如上图所示，在形成一个决策树的过程中需要考虑一些参数，比如说分支数，分支的标准，终止准则，基本假设。

  下面是从图像中得到初音剪影的例子

在这里只是使用了一个单一的决策树，上面是不同深度获得效果，可以看到当树的深度达到20层的时候获得了很好的效果。

2.3 随机森林（Random Forest）

  随机森林便是 bagging 的一个很好的例子，如下图所示

决策树很容易在训练集上获得0错误率的结果，因为如果一个叶子节点对应一个例子的话，很容易会得到这样的结果。这是就要对决策树采用 bagging 的方法，实际上也就是使用了随机森林的方法。在随机森林中仅仅进行重采样是不够的，因为仅仅使用重采样会使训练出的树之间很像；为了树之间更不像，还要决定哪些特性用于分类，哪些特性不用于分类。如上面的表格所示，第一个分类函数仅仅使用 x1,x2 两个数据，后面的都是一样的，只是选择了一些数据，所以在使用验证集的时候可以直接使用那些没有用来训练的数据进行测试，比如说使用f2 +f4组成随机森林，用数据x1进行检验，这种方法叫做 Out-of-bag，他看不在 bag 中的例子的表现如何，来判断现在模型的表现如何，这种方法的一个好处在于，它可以不用再事先切一个验证集出来，直接使用没有被用到的数据进行验证就好，随机森林的一个的实验结果如下图所示

这里总共使用了100个树构成的随机森林，从实验结果中可以看到，较为浅层的树仍然不能获得很好的效果，但是它可以使得结果更为平滑。

3. Ensemble: Boosting

  与 Bagging 有所不同，Boosting的目的不是为了抑制过拟合，而是为了提高弱的分类器的性能。它可以保证，只要你使用的分类器在训练数据上的误差小于50%，通过Boosting 之后你得分类器的正确率最终总会到0。

  Boosting 的具体框架如下

首先他会获得第一个分类器 f1(x) ，然后找到第二个分类器 f2(x) 来帮助第一个分类器 f1(x) 。这个第二个分类器是什么样的机器学习算法都好，只要能够帮到 第一个分类器 f1(x) 提高整体的性能；然而如果 f2(x) 与 f1(x) 是很相似的话，那么它们就没有办法帮助他很多，我们希望我们得到的 f2(x) 与 f1(x) 是互补的。然后我们就得到了第二个分类器 f2(x) ，最后组合所有的分类器。然而这其中有很重要的是，分类器是需要按顺序学习的，不像之前的分类器是可以分开学习的。

3.1 那如何获得不同的分类器呢？

  关键的思想在于获得不同的训练数据。重采样虽然可以获得不同的训练数据，但是每一个数据被采样的次数一定是整数，我们没有办法将一个数据采样2.1次或者0.1次。所以这个时候就要采用对数据重新赋权重的方法来获得不同的数据，如下图所示

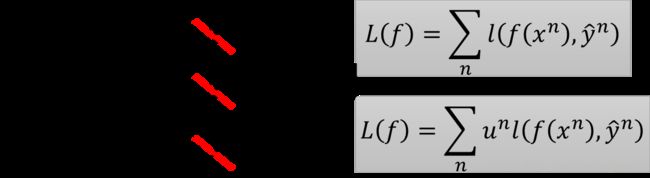
假设原始的权重都是1，更新之后的权重为图中所示的数，那么损失函数也要进行同样的改变，在计算某一个数据的损失值之后还要乘以他的权重。

3.2 Adaboost的思想

  Adaboost的思想在于它使用令分类器 f1(x) 失败的数据进行训练得到 f2(x) ，之所以 f2(x) 所用的数据要使 f1(x) 失败，其主要原因是为了使 f1(x) 和 f2(x) 互补 。那么如何找到这样的数据呢？

  我们定义 f1(x) 在它的训练集上的误差为

分子的部分已经上面说过了，对于分母 Z1 ，他是所有权重的和，上标 n 代表这是第 n 个数据，下标代表这是使用在第几个弱分类器 f(x) ，其中的分类误差是小于0.5的，因为如果分类误差大于0.5，那么直接反过来就好了。

  而所谓的是原来的分类器在新的数据上失败的含义就是，原来的分类器在新的数据集（调整完权重的数据集）上的分类的正确率为50%，即

使 f1(x) 的效果在 f2(x) 所对应的新数据集上如同是在随机猜测一样。一个具体的例子如下图所示

假设原始数据的权重都是1，并且在这个权重下训练出了一个分类器 f1(x) ，这个时候计算分类误差就是0.25。之后我们需要修改训练数据的权重使得 f1(x) 失效（即分类正确率为0.5）。具体做法是将分类正确的数据的权重降低，而将分类错的权重增大，这就使得原来的分类器虽然分类还是正确的，但是经过了加权求和之后，原始分类器的就失效了（正确率只有0.5）。

  所以训练数据的权重更新方法如下图所示

我们将分类正确的数据的权重除以一个大于1的数 d1 ，对于分类错误的数据乘以一个相同的权重 d1 。那这个权重具体怎么算呢？计算的方法如下，具体推导过程省略

其中的 ϵ 是在这个分类函数上的误差，因为 ϵ<0.5 ，所以计算出的 d1>1 。

3.3 Adaboost的算法流程

  以二分类为例，Adaboost的算法流程如下图所示

给定一些训练数据，标签是+1和-1，初始的权重都是1 ，总共由 T 个弱分类器组成 Adaboost。首先使用权重为 ut 的数据训练出第 t 个分类器，这时 ϵt 是用权重为 ut 的数据训练出第 t 个分类器的误差，之后计算 dt 。如果分类正确就除以常数 dt ，如果分类错误就乘以常数 dt ，以此来更新 ut+1 。

  如果将 d1 表示为 αt=ln((1−ϵt)/ϵt−−−−−−−−√) 会使得分类的过程表述为更为简单的形式，参数更新的过程可以表示为

将上述分为两种情况讨论的过程表示为实际标签与预测标签的乘积的一个等式，所以不直接使用 d1 ，而是使用其指数的形式主要是为了计算表达简单清晰。

  在将得到的 N 个模型集成在一起的过程中，有以下两种方法

其中第一种方法“Uniform weight”是等权重地看待每一个的结果，这是一种比较不好的方法，更好的方法是将它们按照权重 αt 组合在一起，如上图“Non-niform weight”所示。这里使用 αt 作为权重直觉上是合理的，因为 αt 越大说明其所对应的弱分类器的错误率越小，也就是说分类效果越好，它就应该具有较大的权重。所以分类器的错误率越小，在最后投票的时候权重就越大。

  下面将以一个具体的例子进行说明，在这里我们总共使用3个分类器，分类器使用只画一条线的 decision stump

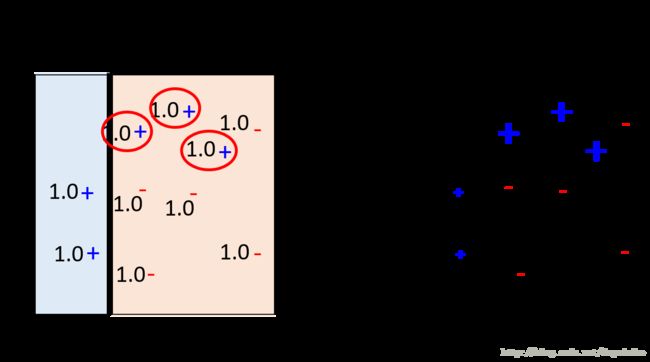
首先进行分类，边界如左图所示，这个时候的误差是0.3，计算 d1 ，之后将分类正确的数据除以 d1 ，将分类正确的乘以 d1 ，更新数据的权重如上图右部分所示，此时第一分类器的权重就是 α1 。

  之后根据跟新权重后的数据训练第二个分类器

之后如图画一条分类的界限，其中左侧被划分为正例，而右侧划分为负例，之后仍然计算错误分类率等参数，并更新训练集数据。其中计算分类率的方法不是将三个0.65相加在除以3，而是相加之后除以全体的权重。

然后将这三个分类器按照权重组合起来，如下图所示

3.4 Adaboost 的相关证明

  在这里我们需要证明的是，随着T的逐渐增加，H(x)在训练集上获得越来越小的错误率。其中

具体过程略。

3.5 Adaboost 训练结果说明

  在使用 Adaboost 的过程中，常常会出现如下的情况

我们可以看到，在训练集上结果很快0错误；但是更为奇怪的是在训练数据已经达到最佳的情况下，继续训练的话仍会提高测试集上的正确率。通过分析模型的函数我们可以发现如下的规律。

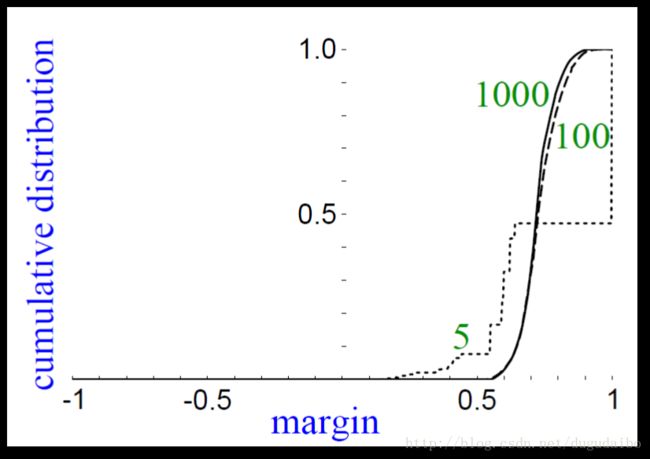
图中的横坐标是 margin ，具体是指函数间距 yg(x) ，其中的 h(x) 是最后得到的强分类器；纵坐标是累计分布，我们可以看到随着迭代次数的增加，分类正确率的曲线随着执行 Adaboost 次数的增多，曲线一直再向右推，意味着再尽力的到越来愈好的结果。

  如下图所示

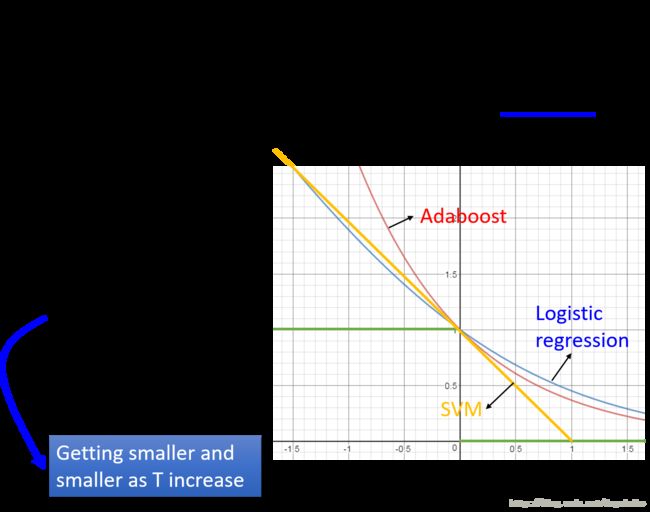
所以虽然看来分类正确率已经达到了100%，但是他的 margin 仍然没有达到最佳，增加 Adaboost 迭代次数仍然会增强模型在测试集上的表现。上面的图表示了不同的损失函数的 up bound ，我们可以看到 Adaboost 即使在分类正确的情况下仍会继续加大的 margin。

  同样对于初音的剪影进行分析，在这里我们使用 Adaboost + Decision Tree 的方法，其中所有的决策树都是深度为 5 的决策树，实验结果如下图所示

4. Ensemble: Stacking

  如果建立了对个模型进行投票的话，常用的一种方法是直接进行等权重的投票，如下图所示

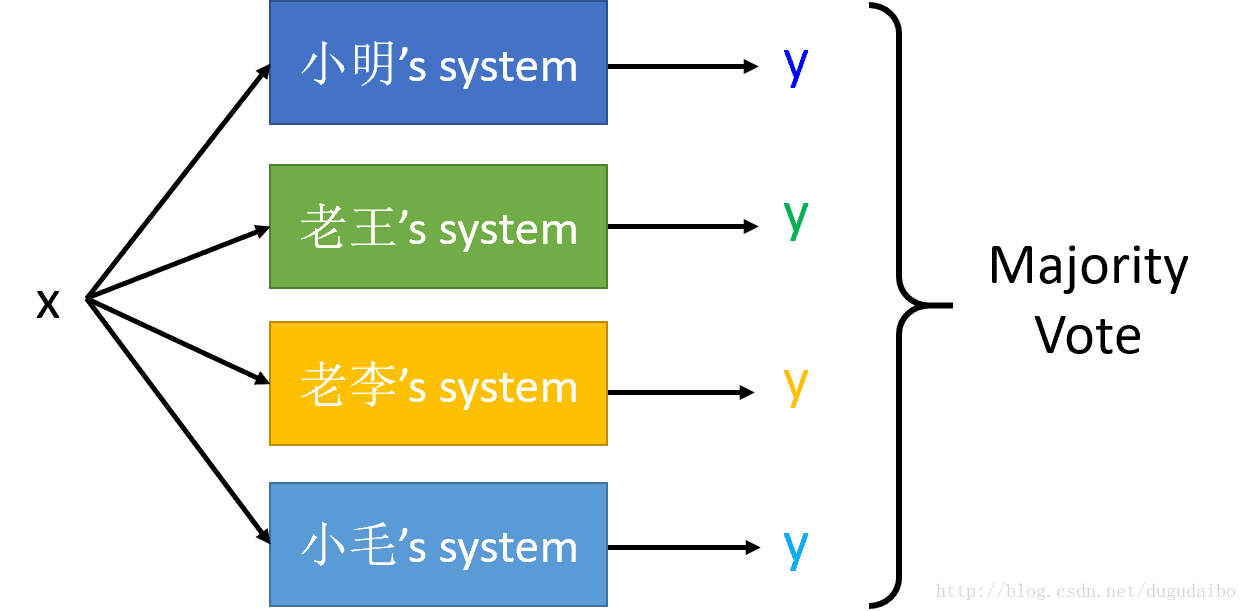
但是如果这个时候小毛的模型是表现最差的，采用等权重的方法进行投票的话，明显会降低整体模型的性能。这个时候就可以采用如下的办法进行改进

我们将这四个模型的输出作为 Final Classifier 的输入，将 Final Classifier 的输出作为最后的分类结果。在训练的过程中，将数据分为如上的四分，使用第一份数据训练这个简单的模型，之后使用黑色的数据输入之前训练的模型，然后再用他们训练 Final Classifier ，这里 Final Classifier 采用的是一个较为简单的模型，比如说逻辑回归。然后再用后面的数据进行验证和测试。