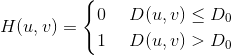数字图像处理第三章——频域处理（下）

数字图像处理—频域处理

（六）高通(锐化)频域滤波器

低通滤波使图像变得模糊那样，相反的处理过程一高通滤波，通过削弱傅立叶变换的低频以及保持高频相对不变来锐化图像。图像锐化是一种补偿轮廓 、突出边缘信息以使图像更为清晰的处理方法 。 锐化的目标实质上是要增强原始图像的高频成分 。与图像平滑不同，图像平滑通过积分过程使图像边模糊，图像锐化则是通过微分过程使图像变清晰。图像锐化的目的：

1. 增强图像边缘，使模糊的图像变得更加清晰，颜色变得鲜明突出，图像的质量有所改善，产生更适合人眼观察和识别的图像；
2. 希望通过锐化处理后，目标物体的边缘鲜明，以便于提取目标的边缘、对图像进行分割、目标区域识别、区域形状提取等，进一步的图像理解与分析奠定基础。

高通滤波器: 理想高通滤波器IHPF；巴特沃思高通滤波器BHPF；高斯高通滤波器GHPF；

高通滤波器的传递函数由下式给出：

6.1 高通滤波函数

使用函数 lpfilter 构建另一个函数hpfilter，使用它可以产生高通滤波器：

function H = hpfilter(typef M, N, DO, n) 
if nargin 4 == 4
  n = 1;
end
Hlp = lpfilter(type, M, N,DO, n); 
H = 1 - Hlp;

下面分别介绍三种滤波器：理想、布特沃斯和高斯高通滤波器的绘图和图像

理想高通滤波器：与低通滤波器相对，IHPF将以D0为半径的圆周内的所有频率置为0，而毫不衰减地通过圆周外的任何频率。 IHPF 也是物理不可实现的，只能通过计算机实现。和ILPF一样有振铃现象 。

函数公式：

编写代码：

H = fftshift(hpfilter('ideal', 500, 500, 50));   %对图像频谱进行移动，使0频率点在中心
figure;
subplot(1, 2, 1), surf(double(H(1:10:500, 1:10:500))), title('理想高通滤波器绘图');
subplot(1, 2, 2), imshow(H,[]), title('理想高通滤波器图像');

代码运行效果如下：

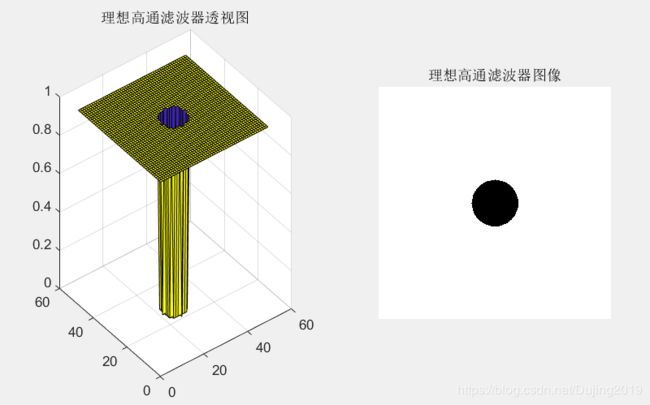
布特沃斯高通滤波器:BHPF比IHPF更平滑，它在高低频之间有比较光滑的过渡；BHPF振铃不明显，对微小物体的过滤比IHPF清晰。

函数公式：

编写代码：

H = fftshift(hpfilter('btw', 500, 500, 50)); 
figure;
subplot(1, 2, 1), surf(double(H(1:10:500, 1:10:500))), title('布特沃斯高通滤波器透视图');
subplot(1, 2, 2), imshow(H,[]), title('布特沃斯高通滤波器图像');

代码运行效果如下：

高斯高通滤波器:GHPF比前2种更平滑，它在高低频之间有光滑的过渡,无振铃效果，对微小物体的过滤更清晰。

函数公式：

编写代码：

H = fftshift(hpfilter('gaussian', 500, 500, 50)); 
figure;
subplot(1, 2, 1), surf(double(H(1:10:500, 1:10:500))), title('高斯高通滤波器透视图');
subplot(1, 2, 2), imshow(H,[]), title('高斯高通滤波器图像');

代码运行效果如下：

下面对比下不同滤波器对图像的处理效果：

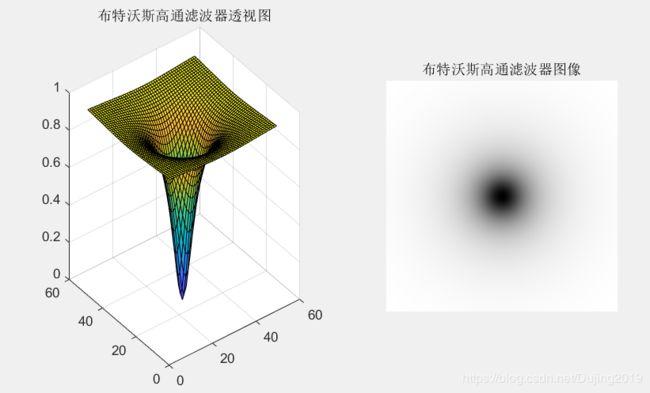
理想高通滤波器：
编写代码：

w = imread('D:\数字图像处理\第三章学习\blackhole.png');
f = im2double(rgb2gray(w));    %把图像变为灰度图像
PQ = paddedsize(size(f));      %获取填充尺寸
[U,V] = dftuv(PQ(1),PQ(2));
DO = 0.05*PQ(2);               %设定滤波器的阈值
F = fft2(f,PQ(1),PQ(2));       %傅里叶变换
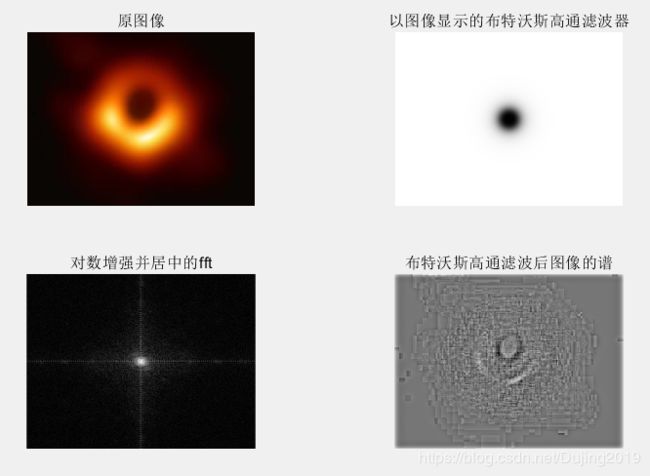
H = hpfilter('ideal', PQ(1),PQ(2), DO, 2);   %理想高通滤波
g = dftfilt(f,H);              %用滤波器对图像进行频域滤波
subplot(2, 2, 1), imshow(w), title('原图像');
subplot(2, 2, 2), imshow(fftshift(H),[]), title('以图像显示的理想高通滤波器');
subplot(2, 2, 3), imshow(log(1+abs(fftshift(F))),[]), title('对数增强并居中的fft');
subplot(2, 2, 4), imshow(g,[]), title('理想高通滤波后图像的谱');

运行代码效果如下：

布特沃斯高通滤波器：
编写代码：

w = imread('D:\数字图像处理\第三章学习\blackhole.png');
f = im2double(rgb2gray(w));    %把图像变为灰度图像
PQ = paddedsize(size(f));      %获取填充尺寸
DO = 0.05*PQ(1);               %设定滤波器的阈值
H = fftshift(hpfilter('btw', PQ(1),PQ(2), DO)); 
g = dftfilt(f,H);
figure;
subplot(1, 3, 1), imshow(w), title('原图像');
subplot(1, 3, 2), imshow(f), title('图像的灰度图像');
subplot(1, 3, 3), imshow(g), title('理想高通滤波后结果');

代码运行效果如下：

高斯高通滤波器：
编写代码：

w = imread('D:\数字图像处理\第三章学习\blackhole.png');
f = im2double(rgb2gray(w));    %把图像变为灰度图像
PQ = paddedsize(size(f));      %获取填充尺寸
[U,V] = dftuv(PQ(1),PQ(2));
DO = 0.05*PQ(2);               %设定滤波器的阈值
F = fft2(f,PQ(1),PQ(2));       %傅里叶变换
H = hpfilter('gaussian', PQ(1),PQ(2), DO, 2); 
g = dftfilt(f,H);              %用滤波器对图像进行频域滤波
subplot(2, 2, 1), imshow(w), title('原图像');
subplot(2, 2, 2), imshow(fftshift(H),[]), title('以图像显示的高斯高通滤波器');
subplot(2, 2, 3), imshow(log(1+abs(fftshift(F))),[]), title('对数增强并居中的fft');
subplot(2, 2, 4), imshow(g,[]), title('高斯高通滤波后图像的谱');

实验结论：不同的滤波器对图像的滤波效果是不同的。它们的共同点是图像在经过高通滤波后，消除了模糊，突出了边缘，使低频分量得到了抑制，从而增强了高频分量，使图像的边沿或线条变得清晰，实现了图像的锐化。但理想高通滤波器出现了明显的振铃现象，即图像边缘有抖动现象；而布特沃斯滤波器高通效果较好，但是计算复杂，其优点是有少量的低频通过，故H(u,v)是渐变的，振铃不明显；高斯高通滤波效果比前两者都要好些，更为平滑，没有振铃现象。而且不同的滤波半径和不同的滤波器阶数对图像的滤波效果也是不同的。滤波半径越越小，则图像的滤波效果越好；滤波器阶数越高，则滤波效果越好。

6.2 高频强调滤波

高通滤波器偏离了 dc的0项，因此减少了图像中平均值为 0的值。 一种补偿方法是为高通滤波器加上偏移量。如果偏移量与将滤波器乘以某个大于 1 的常数结合 起来，这种方法就叫做高频强调滤波，因为这个常量乘数突出了高频部分。这个乘数也增加了 低频部分的幅度，但是只要偏移量与乘数相比较小，低频增强的影响就弱于高频增强的影响。 高频强调滤波有如下传递函数：

a是偏移量，b 是乘数。

下面尝试将将高频强调滤波和直方图均衡化结合起来

编写代码：

w = imread('D:\数字图像处理\第三章学习\blackhole.png');
f = im2double(rgb2gray(w));    %把图像变为灰度图像
PQ = paddedsize(size(f)); 
DO = 0.05*PQ(1);    %，Do的值等于填充过 的图像垂直尺寸的5%
HBW = hpfilter('btw', PQ(1),PQ(2), DO, 2); 
H = 0.5 + 2*HBW;
gbw = dftfilt(f, HBW, 'fltpoint');       %函数 dftfilt 中用 fltpoint 选项以得到浮点结果
gbw = gscale(gbw); 
ghf = dftfilt(f, H, 'fltpoint'); 
ghf = gscale(ghf);
ghe = histeq(ghf, 256); 
subplot(2, 2, 1), imshow(w), title('原图像');
subplot(2, 2, 2), imshow(gbw,[]), title('布特沃斯滤波器滤波后的结果');
subplot(2, 2, 3), imshow(ghf,[]), title('高频强调的结果');
subplot(2, 2, 4), imshow(ghe,[]), title('高频强调后经直方图均衡化结果');

实验结论：(b)图显示了用二阶布特沃斯高通滤波器对图 (a)滤波后的结果，Do的值等于填充过的图像垂直尺寸的5%。假设滤波器的半径不小于通过变换原点附近的频率，高通滤波就不会对Do的值过度敏感。正如预料的那样，滤波的结果并无特色，但却显示出图像的主要边缘有点模糊。如果某些灰度值是负的，仅有一条途径使一幅非 0 图像的平均值为 0。图 (b)的滤波结果就是这种情况。由于这个原因，我们必须在函数 dftfilt 中用 fltpoint 选项以得到浮点结果。如果不这样做，在默认情况下，负值将被裁剪而转换为 uint8 类(输入图像的类)，微弱的细节将丟失。用函数gscale 考虑负值，将会保留这些细节。 高频强调滤波(在这种情况下，a=0.5, b=2.0)的优点显示在图©中，图像中由低频成分引起的灰度色调得以保持。由图可以看出在灰度级窄范围内以灰度为特征的图像直方图均衡化是理想选择。

（七）选择性滤波

7.1带阻和带通滤波器

将低通滤波器和高通滤波器串联，就可以得到带通滤波器。将输入电压同时作用于低通滤波器和高通滤波器，再将两个电路的输出电压求和，就可以得到带阻滤波器。带阻滤波器可以通过高频和低频，但是中频通不过；带通滤波器，能通过中频，但是高频和低频不能通过。

理想带阻滤波器表达式为：

布特沃斯带阻滤波器表达式为：

高斯带阻滤波器表达式为：

带通滤波器表达式与此相反，1减带阻即可。

7.2 陷波带阻和陷波带通滤波器

陷波滤波器也用于去除周期噪声，虽然带阻滤波器也能可以去除周期噪声，但是带阻滤波器对噪声以外的成分也有衰减。而陷波滤波器主要对某个点进行衰减，对其余的成分不损失。

用陷波滤波器减少波纹模式：

w = imread('D:\数字图像处理\第三章学习\blackhole.png');
f = im2double(rgb2gray(w));       %把图像变为灰度图像
[M N] = size(f); 
[f,revertclass] = tofloat(f);     %存储输入的类，以便以后使用。
F = fft2(f);                      %傅里叶变换
S = gscale(log(1+abs(fftshift(F))));
C1 = [99 154;128 163];
H1 = cnotch('gaussian','reject', M,N,C1,5);
P1 = gscale(fftshift(H1).*(tofloat(S)));
g1 = dftfilt(f, H1);   %采用默认值 0 填充边缘，频率域滤波函数，第一个参数为原始图像，后者为二维频率域滤器
figure;
subplot(2, 2, 1), imshow(g), title('原图像');
g1 = revertclass(g1);     
C2 = [99 154;128 163;49 160;133 233;55 132;108 255;112 74];
H2 = cnotch('gaussian','reject',M,N,C2,5);
P2 = gscale(fftshift(H2).*(tofloat(S)));      %用gscale来进行将数据缩放到默认值0~255
g2 = dftfilt(f,H2);
g2 = revertclass(g2);          %revertclass 可以用于把输出转换回与 f 相同的类。
subplot(2, 3, 1), imshow(w), title('原图像');
subplot(2, 3, 2), imshow(S), title('谱');
subplot(2, 3, 3), imshow(P1), title('应用于由波纹模式导致的低频脉冲的陷波滤波器');
subplot(2, 3, 4), imshow(g1), title('滤波结果');
subplot(2, 3, 5), imshow(P2), title('用更多的滤波器消除高频“结构”噪声');
subplot(2, 3, 6), imshow(g2), title('滤波结果');

代码运行效果如下：

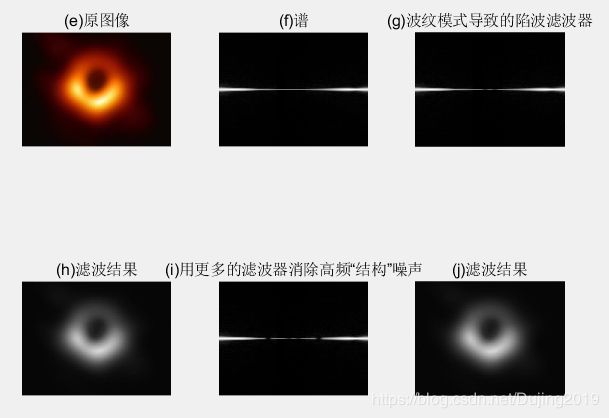
实验结论：在频域中，周期干扰导致很强的局部能量脉冲， 因为干扰相对处于低频，我们开始滤除接近原点的尖刺。使用下面的 cnotch 函数来做。（i)显示了加在谱上的陷波滤波，而(j)图是滤波后的结果。与(h)比较， 我们可以看到高频干扰的减少。虽然这个最终结果远不完美，但相对原始图像来说改进还是有意义的。