字典树-Trie树

一、概念

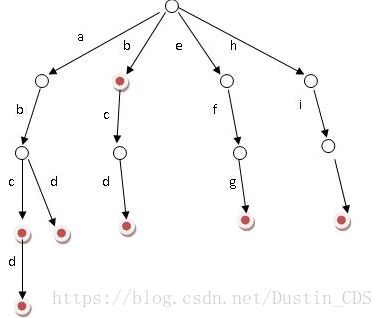
字典树，又称为单词查找树，Tire数，是一种树形结构，它是一种哈希树的变种。利用字符串的公共前缀来减少查询时间，最大限度的减少无谓的字符串比较。

1.1 基本性质

• 根节点不包含字符，除根节点外的每一个子节点都包含一个字符
• 从根节点到某一节点。路径上经过的字符连接起来，就是该节点对应的字符串
• 每个节点的所有子节点包含的字符都不相同

---

1.2 特性

1）根节点不包含字符，除根节点外每一个节点都只包含一个字符。
2）从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
3）每个节点的所有子节点包含的字符都不相同。
4）如果字符的种数为n，则每个结点的出度为n，这也是空间换时间的体现，浪费了很多的空间。
5）插入查找的复杂度为O(n)，n为字符串长度。

---

1.3 基本思想

（1）插入过程
对于一个单词，从根开始，沿着单词的各个字母所对应的树中的节点分支向下走，直到单词遍历完，将最后的节点标记为红色，表示该单词已插入Trie树。

（2）查询过程
同样的，从根开始按照单词的字母顺序向下遍历trie树，一旦发现某个节点标记不存在或者单词遍历完成而最后的节点未标记为红色，则表示该单词不存在，若最后的节点标记为红色，表示该单词存在。

---

-

二、代码实现

2.1 字典树节点定义

class TrieNode {
    private int num;// 有多少单词通过这个节点,即由根至该节点组成的字符串模式出现的次数
    private TrieNode[] son;// 所有的儿子节点
    private boolean isEnd;// 是不是最后一个节点
    private char val;// 节点的值

    TrieNode() {
        num = 1;
        son = new TrieNode[SIZE];
        isEnd = false;
    }
}

---

2.2 字典树构造函数

    // 初始化字典树
    Trie(){
        root = new TrieNode();
    }

---

2.3 建立字典树

    // 建立字典树
    // 在字典树中插入一个单词
    public void insert(String str) {
        if (str == null || str.length() == 0) {
            return;
        }
        TrieNode node = root;
        char[] letters = str.toCharArray();//将目标单词转换为字符数组
        for (int i = 0, len = str.length(); i < len; i++) {
            int pos = letters[i] - 'a';
            if (node.son[pos] == null)  //如果当前节点的儿子节点中没有该字符，则构建一个TrieNode并复值该字符
            {
                node.son[pos] = new TrieNode();
                node.son[pos].val = letters[i];
            } else   //如果已经存在，则将由根至该儿子节点组成的字符串模式出现的次数+1
            {
                node.son[pos].num++;
            }
            node = node.son[pos];
        }
        node.isEnd = true;
    }

---

2.4 在字典树中查找是否完全匹配一个指定的字符串

    // 在字典树中查找一个完全匹配的单词.
    public boolean has(String str) {
        if (str == null || str.length() == 0) {
            return false;
        }
        TrieNode node = root;
        char[] letters = str.toCharArray();
        for (int i = 0, len = str.length(); i < len; i++) {
            int pos = letters[i] - 'a';
            if (node.son[pos] != null) {
                node = node.son[pos];
            } else {
                return false;
            }
        }
        //走到这一步，表明可能完全匹配，也可能部分匹配，如果最后一个字符节点为末端节点，则是完全匹配，否则是部分匹配
        return node.isEnd;
    }

---

2.5 前序遍历字典树

    // 前序遍历字典树.
    public void preTraverse(TrieNode node) {
        if (node != null) {
            System.out.print(node.val + "-");
            for (TrieNode child : node.son) {
                preTraverse(child);
            }
        }
    }

---

2.6 计算单词前缀的数量

    // 计算单词前缀的数量
    public int countPrefix(String prefix) {
        if (prefix == null || prefix.length() == 0) {
            return -1;
        }
        TrieNode node = root;
        char[] letters = prefix.toCharArray();
        for (int i = 0, len = prefix.length(); i < len; i++) {
            int pos = letters[i] - 'a';
            if (node.son[pos] == null) {
                return 0;
            } else {
                node = node.son[pos];
            }
        }
        return node.num;
    }

---

2.7 完整代码

package com.xj.test;

public class Trie {
    private int SIZE = 26;
    private TrieNode root;// 字典树的根

    class TrieNode // 字典树节点
    {
        private int num;// 有多少单词通过这个节点,即由根至该节点组成的字符串模式出现的次数
        private TrieNode[] son;// 所有的儿子节点
        private boolean isEnd;// 是不是最后一个节点
        private char val;// 节点的值

        TrieNode() {
            num = 1;
            son = new TrieNode[SIZE];
            isEnd = false;
        }
    }

    // 初始化字典树
    Trie() {
        root = new TrieNode();
    }

    // 建立字典树
    // 在字典树中插入一个单词
    public void insert(String str) {
        if (str == null || str.length() == 0) {
            return;
        }
        TrieNode node = root;
        char[] letters = str.toCharArray();//将目标单词转换为字符数组
        for (int i = 0, len = str.length(); i < len; i++) {
            int pos = letters[i] - 'a';
            //如果当前节点的儿子节点中没有该字符，则构建一个TrieNode并复值该字符
            if (node.son[pos] == null) {
                node.son[pos] = new TrieNode();
                node.son[pos].val = letters[i];
            }
            //如果已经存在，则将由根至该儿子节点组成的字符串模式出现的次数+1
            else {
                node.son[pos].num++;
            }
            node = node.son[pos];
        }
        node.isEnd = true;
    }

    // 计算单词前缀的数量
    public int countPrefix(String prefix) {
        if (prefix == null || prefix.length() == 0) {
            return -1;
        }
        TrieNode node = root;
        char[] letters = prefix.toCharArray();
        for (int i = 0, len = prefix.length(); i < len; i++) {
            int pos = letters[i] - 'a';
            if (node.son[pos] == null) {
                return 0;
            } else {
                node = node.son[pos];
            }
        }
        return node.num;
    }

    // 打印指定前缀的单词
    public String hasPrefix(String prefix) {
        if (prefix == null || prefix.length() == 0) {
            return null;
        }
        TrieNode node = root;
        char[] letters = prefix.toCharArray();
        for (int i = 0, len = prefix.length(); i < len; i++) {
            int pos = letters[i] - 'a';
            if (node.son[pos] == null) {
                return null;
            } else {
                node = node.son[pos];
            }
        }
        preTraverse(node, prefix);
        return null;
    }

    // 遍历经过此节点的单词.
    public void preTraverse(TrieNode node, String prefix) {
        if (!node.isEnd) {
            for (TrieNode child : node.son) {
                if (child != null) {
                    preTraverse(child, prefix + child.val);
                }
            }
            return;
        }
        System.out.println(prefix);
    }

    // 在字典树中查找一个完全匹配的单词.
    public boolean has(String str) {
        if (str == null || str.length() == 0) {
            return false;
        }
        TrieNode node = root;
        char[] letters = str.toCharArray();
        for (int i = 0, len = str.length(); i < len; i++) {
            int pos = letters[i] - 'a';
            if (node.son[pos] != null) {
                node = node.son[pos];
            } else {
                return false;
            }
        }
        //走到这一步，表明可能完全匹配，可能部分匹配，如果最后一个字符节点为末端节点，则是完全匹配，否则是部分匹配
        return node.isEnd;
    }

    // 前序遍历字典树.
    public void preTraverse(TrieNode node) {
        if (node != null) {
            System.out.print(node.val + "-");
            for (TrieNode child : node.son) {
                preTraverse(child);
            }
        }
    }

    public TrieNode getRoot() {
        return this.root;
    }

    public static void main(String[] args) {
        Trie tree = new Trie();
        String[] strs = {"banana", "band", "bee", "absolute", "acm",};
        String[] prefix = {"ba", "b", "band", "abc",};
        for (String str : strs) {
            tree.insert(str);
        }
        System.out.println(tree.has("abc"));
        tree.preTraverse(tree.getRoot());
        System.out.println();
        //tree.printAllWords();
        for (String pre : prefix) {
            int num = tree.countPrefix(pre);
            System.out.println(pre + "数量:" + num);
        }
    }
}

---

-

三、Trie树的应用

适用范围：数据量大，重复多，但是数据种类小可以放入内存

3.1 字符串的快速检索

字典树的查询时间复杂度是O(logL)，L是字符串的长度。所以效率还是比较高的。

3.1.1 与HashMap的比较

（1）Hash冲突

通过hash函数把所有的单词分别hash成key值，查询的时候直接通过hash函数即可，都知道hash表的效率是非常高的，为O(1)。对于单词查询，如果我们hash函数选取的好，计算量少，且冲突少，那单词查询速度肯定是非常快的。那如果hash函数的计算量相对大呢，且冲突率高呢？这些都是要考虑的因素。

（2）动态查询

另外hash表不支持动态查询，什么叫动态查询，当我们要查询单词apple时，hash表必须等待用户把单词apple输入完毕才能hash查询。当你输入到appl时肯定不可能hash吧。

---

3.1.2 统计词频

例一：

一个文本文件，大约有一万行，每行一个词，要求统计出其中最频繁出现的前10个词，请给出思想，给出时间复杂度分析.

答：先用trie树统计每个词出现的次数，时间复杂度是O(n*le)（le表示单词的平均长度）；

然后是用小顶堆找出出现最频繁的前10个词，时间复杂度是O(n*lg10)。

-

例二：

寻找热门查询

原题：搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来，每个查询串的长度为1-255字节。假设目前有一千万个记录，这些查询串的重复读比较高，虽然总数是1千万，但是如果去除重复和，不超过3百万个。一个查询串的重复度越高，说明查询它的用户越多，也就越热门。请你统计最热门的10个查询串，要求使用的内存不能超过1G。

答：利用trie树，关键字域存该查询串出现的次数，没有出现为0。最后用10个元素的最小推来对出现频率进行排序。

---

3.1.3 字符串去重

1000万字符串，其中有些是相同的(重复)，需要把重复的全部去掉，保留没有重复的字符串。

答：使用hash_map或者trie树。

比如trie树，在构建trie树的过程中，如果某个字符串已经存在于trie中则不输出，否则输出到文本中，这样就可以得到不重复的字符串。

hash_map的速度会要快一些，因为在添加一个字符串的时候，hashmap直接用哈希函数就能定位，然后选择是否写入文件，但是trie树需要在子节点中比较。

trie树对hashmap的优势是，在大量重复的单词中，trie树需要的内存会低一些

---

3.2 前缀相关应用

3.2.1 字符串排序

略

---

3.2.2 最长公共前缀

一个字符串和一个字符串集合的最长公共前缀。

abdh和abdi的最长公共前缀是abd，遍历字典树到字母d时，此时这些单词的公共前缀是abd。

---

3.2.3 求以str为前缀的单词个数

略

---

3.3 求一个数组中任意2个数的最大异或值

这个问题可以用01-字典树很好地解决，即把所有数先按二进制从高到低位看成字符串插入trie；

枚举每个数，作为X，然后去trie里尽可能找每一位与X的二进制位相反的数；

匹配不下去了就返回当前扫描到的最大值 Max(X)，与Max进行比较更新。

代码如下：

class Solution {
public:
    int findMaximumXOR(vector<int>& nums) {
        //首先建立root
        Node* root = new Node();

        //将每个数先插入到Trie树中，构建Trie树
        for(auto x : nums)
            insert(root,x);

        int ans = 0;
        //再遍历一次数组，找到每个元素对应的最大异或值，然后再从中找最大的
        for(auto x : nums)
        {
            int temp = x^query(root,x);
            ans = max(ans,temp);
        }
        return ans;
    }

    struct Node {
        int val;
        Node* ch[2];
        Node() {
            val = 0;
            memset(ch,NULL,sizeof(ch));
        }
    };

    void insert(Node* root,int x)
    {
        int a;
        for(int i=31;i>=0;i--)
        {
            a = (x>>i)&1;
            //如果分支还不存在，就先建立分支
            if(root->ch[a]==NULL)
                root->ch[a] = new Node();
            root = root->ch[a];
        }
        //在x的第0位，将x的值赋给val
        root->val = x;
    }

    int query(Node* root,int x)
    {
        int a;
        for(int i=31;i>=0;i--)
        {
            //a是x的第i位的取反
            a = ((x>>i)&1)^1;
            //向下尽可能找相异的分支
            //如果相异的分支不存在
            if(root->ch[a]==NULL)
                a = (x>>i)&1;
            root = root->ch[a];
        }
        return root->val;      
    }
};

---