后缀树
后缀树,就是把一串字符的所有后缀保存并且压缩的字典树。相对于字典树来说,后缀树并不是针对大量字符串的,而是针对一个或几个字符串来解决问题。比如字符串的回文子串,两个字符串的最长公共子串等等,后面应用会说。
一、建立后缀树
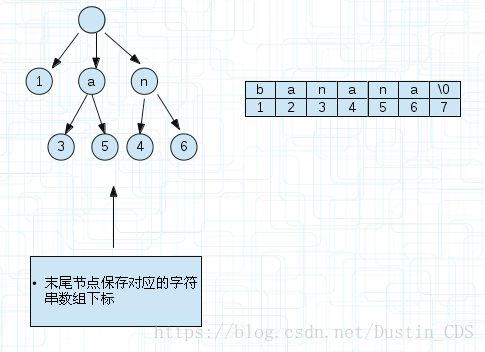
比如单词banana,它的所有后缀显示到下面的。1代表从第一个字符为起点,终点不用说都是字符串的末尾。

以上面的后缀,我们建立一颗后缀树。如下图,为了方便看到后缀,我没有合并相同的前缀。
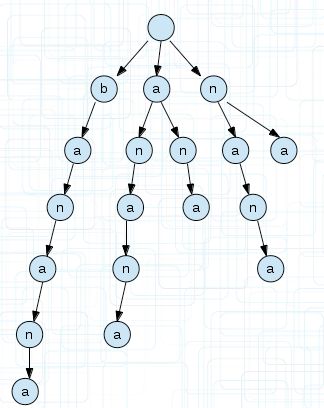
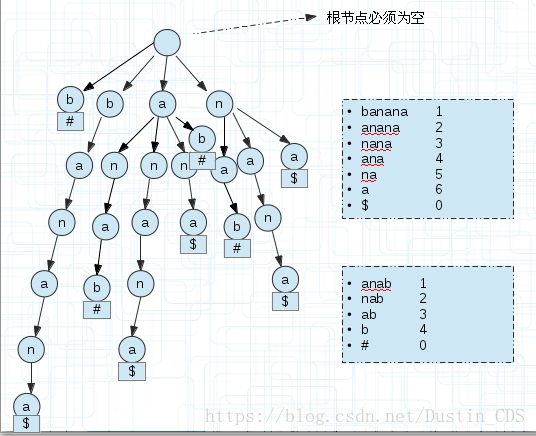
后缀树是把一个字符串所有后缀压缩并保存的字典树,所以我们把字符串的所有后缀还是按照字典树的规则建立,就成了上图的样子。 注意还是和字典树一样,根节点必须为空。
二、压缩后缀树
因为有些后缀串可能是单串,并不和其他的共用同一个前缀。
比如上图中的banana这个后缀串,直接可以用1来表示起点,终点是默认的。
上图的a节点后面有两个节点标记3和5是右边字符数组的下标,对应着a->3-7,a->5-7。因为a是共有的前缀。
三、应用
3.1 判断字符串s1是否是字符串s2的子串
https://blog.csdn.net/heyuchang666/article/details/49784201
如果在后缀树T中查找子串P,我们需要这样的过程:
(1) 从根结点root出发,遍历所有的根的孩子结点:N1,N2,N3….
(2) 如果所有孩子结点中的关键字的第一个字符都和P的第一个字符不匹配,则没有这个子串,查找结束。
(3) 假如N3结点的关键字K3第一个字符与P的相同,则匹配K3和P。
若 K3.length>=P.length 并且K3.subString(0,P.length-1)=P,则匹配成功,否则匹配失败。
若 K3.length<=P.length 并且K3=P.subString(0, K3.length-1),则将子串P1=P.subString(K3.length, P.length); 即取出P中排除K3之后的子串。然后P1以N3为根结点继续重复(1)~(3)的步骤。直到匹配完P1的所有字符,则匹配成功。否则匹配失败。
查询效率:很显然,在上面的算法中。匹配成功正好比较了P.length次字符。而定位结点的孩子指针,和Trie情况类似,假如字母表数量为d。则查询效率为O(d*m),实际上,d是固定常数,如果使用Hash表直接定位,则d=1.
因此,后缀树查询子串P的时间复杂度为O(m),其中m为P的长度。
3.2 获得字符串s1在字符串s2中重复的次数
比如说banana是s1,an是s2,那么计算an出现的次数实际上就是看an是几个后缀串的前缀。
a节点是保存所有起始为a字母的后缀串,我们看a字母后的n字母的引用计数即可。
3.3 两个字符串S1,S2的最长公共部分
先说下广义后缀树,前面说了后缀树可以存储一个或多个字符串,当存储的字符串数量大于等于2时就叫做广义后缀树。
建立一棵广义后缀树,如下图:
$和#是为了区分字符串的。
我们为每个后缀串末尾单独添加一个空间存储区分字符串的符号。那么怎么找s1和s2串最长的公共部分?
遍历每个后缀串,如果其引用计数为1则直接跳过,因为不可能有两个子串存放在这里,当引用计数>1时,往下遍历,直到分叉分别记录子串的符号,如果不同,说明他们是不同字符串的,记录已经匹配的值即可,若相同继续下一次遍历。上图的ana部分,到ana时,子串$结束,然后继续向下,子串anab以#结束,那么匹配了ana。
3.4 最长回文串
把要求的最长回文串的字符串s1和它的反向(逆)字符串s2建立一棵广义后缀树。
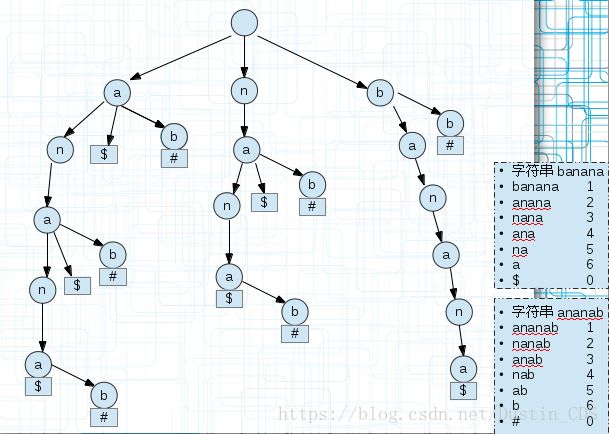
回文串有一个定义就是正反相同,也就是正着和反着可以重和在一起,那么我们直接看这棵广义后缀树的共同前缀即可,每个banana的子串和ananab的子串重合的部分都是回文串,我们只需要找到最长的即可。比如上面的anana,从后面不同的标记可以看出两个字符串的某个后缀都有这个前缀,能完美重合到一起。即它是回文串。
记录Max,每次找到一个回文串比较即可。
四、代码实现
首先定义一个SuffixTree类,用于封装后缀树,内部定义了两个内部类:Node和ActivePoint,分别封装树的节点和算法中提到的活动点。代码结构如下:
public class SuffixTree {
private Node root = new Node(new char[0]);// 根节点
// active point,一个三元组:(active_node,active_edge,active_length)
// active_node是当前的活动点,用节点代表,active_edge是活动的边,这里用节点来表示,active_length是活动的长度
private ActivePoint activePoint = new ActivePoint(root, null, 0);
private int reminder = 0;// remainder,表示还剩多少后缀需要插入
/**
*
* 后缀树的节点,即边
*
*/
private class Node {
public char[] chars;
public Node child;
public Node brother;
public Node suffixNode;
public Node(char[] chars) {
this.chars = chars;
}
}
/**
*
* 活动点(active point),一个三元组:(active_node,active_edge,active_length)
*
*/
private class ActivePoint {
public Node point;
public Node index;
public int length;
public ActivePoint(Node point, Node index, int length) {
this.point = point;
this.index = index;
this.length = length;
}
}
}说明一下,算法中使用了边来保存字符,但是实现时没必要多维护一个类,直接使用节点(Node)来保存字符即可,效果上没有任何差别。同时树的结构通过子节点与兄弟节点的方式保存,如下结构图所示:
父节点
|
子节点—兄弟节点—兄弟节点123采用这种方式的原因是因为一个节点的子节点数量是未知的,所以不适合使用一个固定长度的数组来保存节点的全部子节点,使用集合会造成数据结构嵌套数据结构,不适合。同时根节点也是一个普通节点,只是根节点不存在任何字符(字符数组长度==0)。ActivePoint是一个三元组(包含三个属性),分别对应:活动节点(Node),活动边(Node),活动长度。reminder对应算法中的reminder,记录剩余后缀数量。Node表示一个节点,有4个属性:chars表示该节点上的字符,child和brother是子节点和兄弟节点的指针,suffixNode是后缀连接。
介绍完了整体结构,下面来看看具体如何对一个字符串构建后缀树。
注意:在构建后缀树时使用了一个优化手段,算法中提到每次修改#,使得边上的字符自动扩充一位,在实际实现时我们可直接将从插入字符开始到字符串结束所有的字符全部一次性放到边上,省去每次扩充#。该优化点引用如下(原文见参考文章二):
借助后缀树的特性, 我们可以做出一个相当有效的算法. 首先一个重要的特性是: 一朝为叶, 终生为叶. 一个叶节点自诞生以后绝不会有子孙. 更重要的是, 每当我们往树上加入一个新的前缀, 每一条通往叶节点的边都会延长一个字符(新前缀的最后一个字符). 这使得处理通往叶节点的边变得异常简单, 我们完全可以在创建叶节点的时候就把当前字符到文本末的所有字符一股脑塞进去. 是的, 我们不需要知道后面的字符是啥, 但我们知道它们最终都要被加进去. 因此, 一个叶节点诞生的时候, 也正是它可以被我们遗忘的时候. 你可能会担心通往叶节点的边被分割了怎么办, 那也不要紧, 分割之后只是起点变了, 尾部该怎么着还是怎么着。
/**
* 构建后缀树
*
* @param word
*/
public void build(String word) {
int index = 0;
char[] chars = word.toCharArray();
while (index < chars.length) {// 循环建立后缀
int currenctIndex = index++;// 保存当前的位置
char w = chars[currenctIndex];// 当前的后缀字符
this.print();// 打印
System.out.println();
System.out.println("当前插入后缀:" + w + "========");
if (find(w)) {// 查找是否存在保存有当前后缀字符的节点
reminder++;// 存在,则将reminder+1,activePoint.length+1,然后返回即可
continue;
}
// 不存在的话,如果reminder==0表示之前在该字符之前未剩余有其他带插入的后缀字符,所以直接插入该后缀字符即可
if (reminder == 0) {
// 直接在当前活动节点插入一个节点即可
// 这里插入的节点包含的字符是从当前字符开始该字符串剩余的全部字符,这里是一个优化,
// 优化参考自:http://blog.csdn.net/v_july_v/article/details/6897097 (3.6、归纳, 反思, 优化)
Node node = new Node(Arrays.copyOfRange(chars, currenctIndex, chars.length));
// 如果当前活动点无子节点,则将新建的节点作为其子节点即可,否则循环遍历子节点(通过兄弟节点进行保存)
Node child = activePoint.point.child;
if (null == child) {
activePoint.point.child = node;
} else {
while (null != child.brother) {
child = child.brother;
}
child.brother = node;
}
} else {
// 如果reminder>0,则说明该字符之前存在剩余字符,需要进行分割,然后插入新的后缀字符
Node splitNode = activePoint.index;// 待分割的节点即为活动边(active_edge)
// 创建切分后的节点,放到当前节点的子节点
// 该节点继承了当前节点的子节点以及后缀节点信息
Node node = new Node(Arrays.copyOfRange(splitNode.chars, activePoint.length, splitNode.chars.length));// 从活动边长度开始截取剩余字符作为子节点
node.child = splitNode.child;
node.suffixNode = splitNode.suffixNode;
splitNode.child = node;
splitNode.suffixNode = null;
// 创建新插入的节点,放到当前节点的子节点(通过子节点的兄弟节点保存)
Node newNode = new Node(Arrays.copyOfRange(chars, currenctIndex, chars.length));// 插入新的后缀字符
splitNode.child.brother = newNode;
splitNode.chars = Arrays.copyOfRange(splitNode.chars, 0, activePoint.length);// 修改当前节点的字符
// 分割完成之后需根据规则1和规则2进行区分对待
// 按照规则1进行处理
if (root == activePoint.point) {// 活动节点是根节点的情况
// activePoint.point == root
// 按照规则3进行处理
} else if (null == activePoint.point.suffixNode) {// 无后缀节点,则活动节点变为root
activePoint.point = root;
} else {// 否则活动节点变为当前活动节点的后缀节点
activePoint.point = activePoint.point.suffixNode;
}
// 活动边和活动边长度都重置
activePoint.index = null;
activePoint.length = 0;
// 递归处理剩余的待插入后缀
innerSplit(chars, currenctIndex, splitNode);
}
}
}在SuffixTree中定义一个build(String word)方法,参数word是待生成后缀树的字符串。首先将字符串转成字符数组,并按照算法步骤逐个插入。find(char w)用于查找指定的后缀是否存在(这里所说的后缀其实就是单个字符,因为单个字符代表的就是以该字符开头的后缀)。
/**
* 寻找当前活动点的子节点中是否存在包含后缀字符的节点(边)
*
* @param w
* @return
*/
private boolean find(char w) {
final Node start = activePoint.point;
final Node current = activePoint.index;
boolean exist = false;
if (null == current) {// current==null 无活动边,则从活动点的子节点开始查找
// 寻找子节点
Node child = start.child;
while (null != child) {
if (child.chars[0] == w) {// 存在
activePoint.index = child;
activePoint.length++;// activePoint.length++
exist = true;
break;
} else {
child = child.brother;
}
}
} else if (current.chars[activePoint.length] == w) {// 有活动边,则在活动边上查找
activePoint.length++;
exist = true;
if (current.chars.length == activePoint.length) {
// 如果活动边的长度已达到活动边的最后一个字符,则将活动点置为活动边,同时活动边置为null,长度置为0
activePoint.point = current;
activePoint.index = null;
activePoint.length = 0;
}
} else {
exist = false;
}
return exist;
}查找后缀是否存在是从活动节边开始查找,如果活动边为NULL,则从活动节点的子节点挨个查找,查找是通过比较边上的指定位置(活动长度指定)与查找字符是否相等。这里有个地方需要注意:算法中提到,如果一个活动边已到达结尾(即活动长度==活动边的字符长度),则将活动边晋升为活动节点,并重置活动边和活动长度为NULL和0。如下代码所示:
if (current.chars.length == activePoint.length) {
// 如果活动边的长度已达到活动边的最后一个字符,则将活动点置为活动边,同时活动边置为null,长度置为0
activePoint.point = current;
activePoint.index = null;
activePoint.length = 0;
}如果查找到后缀存在,则直接将活动长度+1(在find()方法内部处理的),reminder+1即可。
if (find(w)) {// 查找是否存在保存有当前后缀字符的节点
reminder++;// 存在,则将reminder+1,activePoint.length+1,然后返回即可
continue;
}如果不存在,需区分两种情况,一种是:前面没有堆积未插入的后缀,即reminder==0,另外一种是reminder>0。
对于reminder==0(如算法中举例的前三个字符abc),只需要直接将当前后缀插入到活动节点即可。具体首先新建一个节点,Node node = new Node(Arrays.copyOfRange(chars, currenctIndex, chars.length));,该节点包含从当前字符往后所有的字符,即上面提到的优化点;接着将新建的节点作为活动节点的子节点插入,这里需判断子节点是否存在,不存在,作为子节点,存在则作为子节点的最后一个兄弟节点。
Node child = activePoint.point.child;
if (null == child) {
activePoint.point.child = node;
} else {
while (null != child.brother) {
child = child.brother;
}
child.brother = node;
}如果reminder>0(如算法中举例步骤6,插入第四到第六个字符abx,到达x时就是这种情况),我们需要对当前活动边进行分割操作。
// 如果reminder>0,则说明该字符之前存在剩余字符,需要进行分割,然后插入新的后缀字符
Node splitNode = activePoint.index;// 待分割的节点即为活动边(active_edge)
// 创建切分后的节点,放到当前节点的子节点
// 该节点继承了当前节点的子节点以及后缀节点信息
Node node = new Node(Arrays.copyOfRange(splitNode.chars, activePoint.length, splitNode.chars.length));// 从活动边长度开始截取剩余字符作为子节点
node.child = splitNode.child;
node.suffixNode = splitNode.suffixNode;
splitNode.child = node;
splitNode.suffixNode = null;
// 创建新插入的节点,放到当前节点的子节点(通过子节点的兄弟节点保存)
Node newNode = new Node(Arrays.copyOfRange(chars, currenctIndex, chars.length));// 插入新的后缀字符
splitNode.child.brother = newNode;
splitNode.chars = Arrays.copyOfRange(splitNode.chars, 0, activePoint.length);// 修改当前节点的字符分割的节点是活动边指向的节点,分割的位置由活动长度指定。具体分割是新建一个节点A,该节点的字符是被分割节点分割之后剩余的字符(’cabx’),同时该节点需继承被分割节点的子节点信息,以及后缀连接信息;再新建一个节点B存放当前要插入的后缀(’x’)。以上两个新建的节点都将作为被分割节点的子节点存在,所以A的兄弟节点指向B,并将被分割节点的字符切去只剩活动长度指定的字符(’ab’)。分割完之后需要根据规则1和规则3重置活动点信息,但是不管活动节点如何设定,活动边和活动边长度必须要重置为NULL和0。
// 分割完成之后需根据规则1和规则3进行区分对待
// 按照规则1进行处理
if (root == activePoint.point) {// 活动节点是根节点的情况
// activePoint.point == root
// 按照规则3进行处理
} else if (null == activePoint.point.suffixNode) {// 无后缀节点,则活动节点变为root
activePoint.point = root;
} else {// 否则活动节点变为当前活动节点的后缀节点
activePoint.point = activePoint.point.suffixNode;
}
// 活动边和活动边长度都重置
activePoint.index = null;
activePoint.length = 0;到这里我们只是插入了后缀’abx’,由于reminder==2,还需要插入’bx’和’x’,所以引入一个递归方法:innerSplit(char[] chars, int currenctIndex, Node prefixNode),用于插入’bx’和’x’。方法有三个参数:chars是构建后缀树的字符串的字符数组,currenctIndex是我们当前插入后缀的位置(for循环的位置),prefixNode是前一次进行分割的节点。所以此处分割完之后需调用innerSplit()方法处理剩余后缀。
// 递归处理剩余的待插入后缀
innerSplit(chars, currenctIndex, splitNode);第三个参数传入splitNode,即将当前被分割的节点传入方法。下面看看innerSplit()如何递归如何剩余后缀。
/**
* 处理剩余的待插入后缀
* @param chars 构建后缀树的全部字符
* @param currenctIndex 当前已处理到的字符位置
* @param prefixNode 前继节点,即已经进行分割的节点,用于标识后缀节点
*/
private void innerSplit(char[] chars, int currenctIndex, Node prefixNode) {
// 此处计算剩余待插入的后缀的开始位置,例如我们需要插入三个后缀(abx,bx,x),已处理了abx,则还剩余ba和x,则下面计算的位置就是b的位置
int start = currenctIndex - reminder + 1;
this.print();// 打印
System.out.println();
System.out.println("当前插入后缀:" + String.copyValueOf(chars, start, currenctIndex - start + 1) + "========");
// dealStart表示本次插入我们需要进行查找的开始字符位置,因为由于规则2,可能出现通过后缀节点直接找到活动节点的情况
// 如通过ab节点的后缀节点,直接找到节点b,那么此时的activePoint(node[b], null, 0),我们需要从node[b]开始查找x,dealStart的位置就是x的位置
int dealStart = start + activePoint.point.chars.length + activePoint.length;
// 从dealStart开始查找所有后缀字符是否都存在(相对与活动点)
for (int index = dealStart; index <= currenctIndex; index++) {
char w = chars[index];
if (find(w)) {// 存在,则查找下一个,activePoint.length+1,这里不增加reminder
continue;
}
Node splitNode = null;// 被分割的节点
if(null==activePoint.index){// 如果activePoint.index==null,说明没有找到活动边,那么只需要在活动节点下插入一个节点即可
// --此处代码build()方法插入节点部分--
}else{
// 开始分割,分割部分同上面的分割
// --此处代码build()方法分割部分--
// 规则2,连接后缀节点
prefixNode.suffixNode = splitNode;
}
// --
reminder--;
// 分割完成之后需根据规则1和规则3进行区分对待
// --代码同build()代码部分--
if(reminder > 0){// 如果reminder==0则不需要继续递归插入后缀
innerSplit(chars, currenctIndex, splitNode);
}
}
}上面代码为了消减篇幅省去了与build()方法重复的代码(完整代码会放到Github上),其实基本逻辑是一样的,只是所处理的方式略有不同,所以没法放到一起。
这里说一下start和dealStart这两个变量的用处。start是本次需要插入的后缀的开始位置,如’bx’,则start就是b的位置,通过reminder获得;dealStart是下面的for循环开始的位置,也就是需要查找后缀的位置,dealStart的出现是由于规则2的存在,如果没有规则2,那么dealStart就是start了,由于规则2活动节点会从root直接跳到一个节点,而无需进行查找,所以如果发生了跳转,比如字符串时’abcabxabcd’,待插入后缀是’bcd’时,这时就是根据规则2直接跳到一个节点b,所以要从’c’开始找,就是因为节点b为我们省了一个字符,所以说后缀连接是用于优化的。prefixNode.suffixNode = splitNode;就是将之前被分割的节点的后缀连接指向当前被分割的节点。
剩余的部分就是查找,分割了,同build()的代码一样,所以省去了。最后,如果本次处理完reminder依旧>0,那么就需要进行递归调用该方法了。
到这里构建后缀树就完成了。下面介绍后缀树的一个应用:查找子串。具体看代码:
/**
* 查找给定字符串是否是其子串
*
* @param word
* @return
*/
public boolean select(String word) {
char[] chars = word.toCharArray();
int index = 0;// 查找到的节点的匹配的位置
// 查找从根节点开始,遍历子节点
Node start = root;
for (int i = 0; i < chars.length; i++) {
if (start.chars.length < index + 1) {// 如果当前节点已匹配完,则从子节点开始,同时需重置index==0
index = 0;
start = start.child;
while (null != start) {
// 比较当前节点指定位置(index)的字符是否与待查找字符一致
// 由于是遍历子节点,所以如果不匹配换个子节点继续
if (start.chars[index] == chars[i]) {
index++;
break;
} else {
start = start.brother;
}
}
if (null == start) {// 子节点遍历完都无匹配则返回false
return false;
}
} else if (start.chars[index] == chars[i]) {
// 如果当前查找到的节点的还有可比较字符,则进行比较,如果不同则直接返回false
index++;
} else {
return false;
}
}
return true;
}由于每个节点包含的字符数不确定,所以需要一个额外的索引记录当前匹配节点中字符的位置。查找的主要思想是先从根节点的字节点开始,挨个找,找不到则不是子串,找到一个节点后从节点上的所有字符挨个匹配,匹配不上则没有,匹配完了,就从这个节点的子节点继续找。
完整代码看这里Github