分组聚集的K-means算法应用实例

概述

在许多实际应用中，需要对许多数据点进行分组，划分成一个个簇（cluster），并计算出每一个簇的中心。这就是著名的k-means算法。

k-means算法的输入是N个d维数据点：x_1, …, x_N，以及需要划分的簇的数目k。算法运行的结果是每个簇的中心点m_1, …, m_k，也可以输出每个簇中有哪些数据点。算法先通过随机，或启发式搜索，确定初始的中心点位置。再通过如下两个步骤的交替，进行数据的计算： 
1.数据点划分。根据当前的k个中心点，确定每个中心点所在的簇中的数据点有哪些。即根据当前的中心点的坐标，计算每个点到这些中心点的距离，选取最短的距离相应的簇为该点所在的簇； 
2.重新计算中心点：根据每个簇中所有点的坐标，求平均值得到这个簇的新的中心。

此算法不一定收敛，因此通常会选取不同的初始点多次运行算法。

k-means算法可以并行化。使用主从模式，由一个节点负责数据的调度和划分，其他各节点负责本地的中心点的计算，并把结果发送给主节点。因此，可以使用MPI并行编程来实现。大致的过程如下： 
1.节点P_0把数据点集划分成p个块：D_1, …,D_p，分配给P_1, …,P_p这个p个节点； 
2.P_0产生初始的k个中心点(m_1, …, m_k)，并广播给所有的节点； 
3.节点P_r计算块D_r中每个点到k个中心点(m_1, …, m_k)的距离，选取最小值对应的中心点为该点所在的簇。 
4.节点P_r分别计算出本地数据点集D_r在每个簇中的总和以及数目，发送给P_0； 
5.P_0收到所有这些数据后，计算出新的中心点(m_1, …, m_k)，广播给所有节点； 
6.重复3-5步直到收敛。

问题描述

K-Means算法主要解决的问题如下图所示。我们可以看到，在图的左边有一些点，我们用肉眼可以看出来有四个点群，但是我们怎么通过计算机程序找出这几个点群来呢？于是就出现了我们的K-Means算法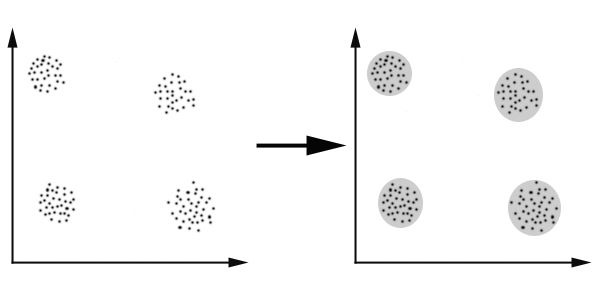 

算法概要

这个算法其实很简单，如下图所示： 
 
K-Means 算法概要

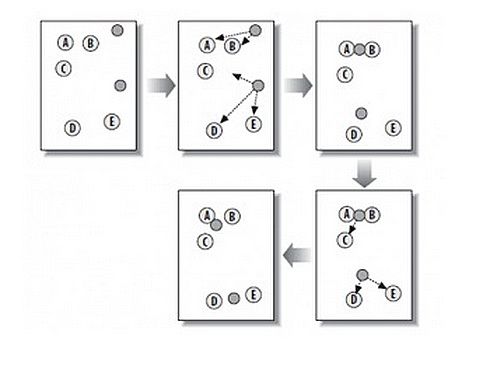
从上图中，我们可以看到， A, B, C, D, E 是五个在图中点。而灰色的点是我们的种子点，也就是我们用来找点群的点 。有两个种子点，所以K=2。

然后，K-Means的算法如下：

随机在图中取K（这里K=2）个种子点。 
然后对图中的所有点求到这K个种子点的距离，假如点Pi离种子点Si最近，那么Pi属于Si点群。（上图中，我们可以看到A,B属于上面的种子点，C,D,E属于下面中部的种子点） 
接下来，我们要移动种子点到属于他的“点群”的中心。（见图上的第三步） 
然后重复第2）和第3）步，直到，种子点没有移动（我们可以看到图中的第四步上面的种子点聚合了A,B,C，下面的种子点聚合了D，E）。 
这个算法很简单，但是有些细节我要提一下，求距离的公式我不说了，大家有初中毕业水平的人都应该知道怎么算的。我重点想说一下“求点群中心的算法”

求点群中心的算法

一般来说，求点群中心点的算法你可以很简的使用各个点的X/Y坐标的平均值。不过，我这里想告诉大家另三个求中心点的的公式：

1）Minkowski Distance 公式 —— λ 可以随意取值，可以是负数，也可以是正数，或是无穷大。

2）Euclidean Distance 公式 —— 也就是第一个公式 λ=2 的情况

3）CityBlock Distance 公式 —— 也就是第一个公式 λ=1 的情况

这三个公式的求中 
心点有一些不一样的地方，我们看下图（对于第一个 λ 在 0-1之间）。 
K-Means ++ 算法

K-Means主要有两个最重大的缺陷——都和初始值有关：

K 是事先给定的，这个 K 值的选定是非常难以估计的。很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适。（ ISODATA 算法 通过类的自动合并和分裂，得到较为合理的类型数目 K） 
K-Means算法需要用初始随机种子点来搞，这个随机种子点太重要，不同的随机种子点会有得到完全不同的结果。（ K-Means++算法 可以用来解决这个问题，其可以有效地选择初始点） 
我在这里重点说一下 K-Means++算法步骤：

先从我们的数据库随机挑个随机点当“种子点”。 
对于每个点，我们都计算其和最近的一个“种子点”的距离D( x )并保存在一个数组里，然后把这些距离加起来得到Sum(D( x ))。 
然后，再取一个随机值，用权重的方式来取计算下一个“种子点”。这个算法的实现是，先取一个能落在Sum(D( x ))中的随机值Random，然后用Random -= D( x )，直到其<=0，此时的点就是下一个“种子点”。 
重复第（2）和第（3）步直到所有的K个种子点都被选出来。 
进行K-Means算法。

算法应用实例

批量图像数据，数据以时间记录 C# 实现代码片段：

“` 
//计算方法 
public class K_mean 
{ 
public List List { get; set; }

        public double Average { get { return List.Average(); } }

        public double Center { get; set; }

        public double Change { get; private set; }
        public double S2 { get; set; }//标准差

        public K_mean()
        {
            Change = double.MaxValue;
            List = new List();
            S2 = 1;
        }

        public void RefreshCenter()
        {
            Change = Math.Abs(Average - Center);
            Center = Average;
        }
        public void RefreshS2()
        {
            double tempS2 = 0;
            for (int j = 0; j < this.List.Count; j++)
            {
                tempS2 = tempS2 + (this.List[j] - Average) * (this.List[j] - Average);
            }
            S2 = Math.Sqrt(tempS2 / this.List.Count);
        }
    }