Datawhale编程学习之栈和队列(2)
文章目录
- 1.学习目标
- 1.1 栈
- 1.2 队列
- 1.3 递归
- 1.4 LeetCode练习题
- 2.学习过程
- 2.1 栈
- 2.2 队列
- 2.3 递归
- 2.4 LeetCode练习题
- 3.参考链接
任务2: 3~4天
1.学习目标
1.1 栈
用数组实现一个顺序栈
用链表实现一个链式栈
编程模拟实现一个浏览器的前进、后退功能
1.2 队列
用数组实现一个顺序队列
用链表实现一个链式队列
实现一个循环队列
1.3 递归
编程实现斐波那契数列求值 f(n)=f(n-1)+f(n-2)
编程实现求阶乘 n!
编程实现一组数据集合的全排列
1.4 LeetCode练习题
栈
Valid Parentheses(有效的括号,第20题,难度:Easy)
英文版:Loading…
中文版:Loading…
Longest Valid Parentheses(最长有效的括号,第32题,难度,hard)
英文版:Loading…
中文版:Loading…
Evaluate Reverse Polish Notatio(逆波兰表达式求值,第150题,难度:Medium)
英文版:Loading…
中文版:Loading…
队列
Design Circular Deque(设计一个双端队列,第641题,难度:Medium)
英文版:Loading…
中文版:Loading…
Sliding Window Maximum(滑动窗口最大值,第239题,难度,Hard)
英文版:Loading…
中文版:Loading…
递归
Climbing Stairs(爬楼梯,第70题,难度:Easy)
英文版:Loading…
中文版:Loading…
2.学习过程
2.1 栈
首先应该明确栈的概念及特点,所谓栈,就是一种容器,其中添加移除新项总发生在同一端。这一端通常称为“顶部”。与顶部对应的端称为“底部”。
最重要特性:先进后出。这一特性让栈拥有反转元素顺序的功能。
2.1.1用数组实现一个顺序栈
栈作为一个先进后出的数据结构,具有压栈、弹栈、取栈顶元素、加入元素、判断为空以及获取栈中元素的方法。而为了实现这些功能,我们可以通过数组和链表来完成。Python的list及其操作可以提供与栈的使用方式有关的功能,可以使用list来实现栈。这里我们默认list末尾为栈顶。
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item): # 进栈
self.items.append(item)
def pop(self): #弹出
return self.items.pop()
def peek(self): # 打印栈顶元素
return self.items[len(self.items)-1]
def size(self):
return len(self.items)
2.1.2用链表实现一个链式栈
链式栈自然就以表头为栈顶
class ListNode:
def __init__(self, elem, next=None):
self.elem = elem
self.next = next
class LStack():
def __init__(self):
self._top = None
def isEmpty(self):
return self._top is None
def push(self, elem):
self._top = ListNode(elem, self._top)
def pop(self):
if self._top is None:
raise ValueError('wrong in pop!')
p = self._top
self._top = p.next
return p.elem
def peek(self):
if self._top is None:
raise ValueError('wrong in peek!')
return self._top.elem
def __repr__(self) -> str:
cur = self._top
nums = []
while cur:
nums.append(cur._data)
cur = cur._next
return "--> ".join(f"{num}" for num in nums)
if __name__ == '__main__':
stack = LStack()
for i in range(10):
stack.push(i)
print(stack)
采用数组实现栈和采用链表实现栈对比:
采用数组实现栈的优点:一个元素值占用一个存储空间;它的缺点为:如果初始化申请的存储空间太大,会造成空间的浪费,如果申请的存储空间太小,后期会经常需要扩充存储空间,扩充存储空间是个费时的操作,这样会造成性能的下降。
采用链表实现栈的优点是:使用灵活方便,只有在需要的时候才会申请空间,它的缺点为:除了要存储元素外,还需要额外的存储空间存储指针信息。
2.1.3编程模拟实现一个浏览器的前进、后退功能
class Browser():
def __init__(self):
self.x = LStack() # 前进
self.y = LStack() # 后退
def view(self, page):
print('Viewing %s' % page, end='\n')
self.x.push(page)
def forward(self):
if self.y.isEmpty():
print( 'can not forward!')
return
top = self.y.pop()
self.x.push(top)
print('go to %s' % top, end='\n')
def backward(self):
if self.x.isEmpty():
print('can not backward!')
return
top = self.x.pop()
self.y.push(top)
print('back to %s' % top, end='\n')
def can_forward(self):
if self.y.isEmpty():
return False
return True
def can_back(self):
if self.x.isEmpty():
return False
return True
if __name__ == '__main__':
b = Browser()
for i in ['a', 'b', 'c']:
b.view(i)
while b.can_back():
b.backward()
while b.can_forward():
b.forward()
b.forward()
2.2 队列
所谓队列,就是一种先进先出的数据结构
2.2.1 用数组实现一个顺序队列
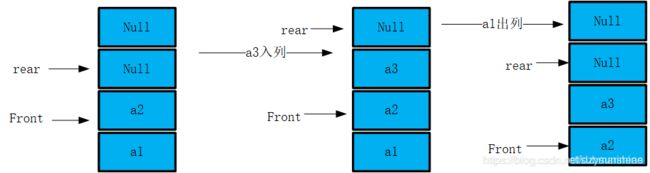
下面给出了一种最简单的实现方式,用front来记录队列首元素的位置,用rear来记录队列尾元素往后一个位置。入队列的时候只需要将待入队列放入下标为rear位置,然后同时执行rear+,那么出队列就是front+。
class MyQueue(object):
"""队列"""
def __init__(self):
self.items = []
self.front = 0 # 队列头
self.rear = 0 # 队列尾
def is_empty(self):
"""判断队列是否为空"""
return self.items == self.rear
def enQueue(self, item):
"""进队列,从队尾加入"""
self.items.append(item)
self.rear += 1
# self.items.insert(0,item) # 从对头进
def deQueue(self):
"""出队列,从队头出"""
if self.rear > self.front:
self.front += 1
else:
print("队列已经为空")
# return self.items.pop() # 从对尾出
def getFront(self):
if self.is_empty():
return None
return self.items[self.front]
def getBack(self):
if self.is_empty():
return None
return self.items[self.rear-1]
def size(self):
"""返回大小"""
return self.rear - self.front
# return len(self.items) # 看大小
2.2.2 用链表实现一个链式队列
采用链表实现队列的方法与实现栈的方法类似,分别用两个指针指向队列的首元素与尾元素,而用pHead来指向队列的首元素,用pEnd来指向队列的尾元素。

class LNode(object):
def __init__(self,x):
self.data = x
self.next = None
class MyQueue(object):
def __init__(self):
"""分配头结点"""
self.pHead = None
self.pEnd = None
def is_empty(self):
"""判断是否为空"""
if self.pHead == None:
return True
return False
def size(self):
"""获取队列的大小"""
size=0
p = self.pHead
while p != None:
# while p is not None:
p = p.next
size += 1
return size
def enQueue(self, element):
"""入队列,从队尾加"""
p = LNode(element)
p.data = element
p.next = None
if self.pHead == None:
self.pHead = self.pEnd=p
else:
self.pEnd.next = p
self.pEnd = p
def deQueue(self):
"""出队列,删除首元素"""
if self.pHead == None:
print("出队列失败,队列已经为空")
self.pHead = self.pHead.next
if self.pHead == None:
self.pEnd = None
def getFront(self):
"""返回队列首元素"""
if self.pHead == None:
print("获取队列首元素失败,队列已经为空")
return None
return self.pHead.data
def getBack(self):
"""返回队列尾元素"""
if self.pEnd == None:
print("获取队列尾元素失败,队列已经为空")
return None
return self.pEnd.data
和栈中的优缺点类似,但与栈不同的是,对于队列,用链表的方式比数组更好,因为指针空间在这里的发挥空间更大。
2.2.3 实现一个循环队列
前面说的顺序队列显然不够高效,如果我们要实现所有操作都是O(1)时间,可以再设置一个指针,记住队头的位置,当出队操作完成后,更新队头指针。
基于上述思想,同时为了防止内存空置消耗,可以采用循环队列的实现。
# coding=utf-8
# @author: kaiyuan
# blog: https://blog.csdn.net/Kaiyuan_sjtu
from itertools import chain
class CirQueue:
def __init__(self, capacity):
self._items = []
self._capacity = capacity + 1
self._head = 0
self._rear = 0
def enqueue(self, elem):
if (self._rear + 1) % self._capacity == self._head:
return False
self._items.append(elem)
self._rear = (self._rear + 1) % self._capacity
return True
def dequeue(self):
if self._head != self._rear:
item = self._items[self._head]
self._head = (self._head + 1) % self._capacity
return item
def __repr__(self):
if self._rear >= self._head:
return " ".join(item for item in self._items[self._head: self._rear])
else:
return " ".join(item for item in chain(self._items[self._head:], self._items[:self._rear]))
if __name__ == '__main__':
cq = CirQueue(10)
for i in range(10):
cq.enqueue(str(i))
print(cq)
for i in range(5):
cq.dequeue()
print(cq)
2.3 递归
2.3.1 编程实现斐波那契数列求值 f(n)=f(n-1)+f(n-2)
class Solution:
def Fibonacci(self, n):
a = [0,1]
if n<=1:
return a[n]
else:
for i in range(2,n+1):
a.append(a[i-1]+a[i-2])
return a[n]
2.3.2 编程实现求阶乘 n!
def factorial(x):
result = 1
for i in xrange(2, x + 1):
result *= i
return result
2.3.3 编程实现一组数据集合的全排列
举个例子,比如你要对a,b,c三个字符进行全排列,那么它的全排列有abc,acb,bac,bca,cba,cab这六种可能,你们想想你们是如何得出这六种可能的。没错!就是当指针指向第一个元素a时,它可以是其本身a(即和自己进行交换),还可以和b,c进行交换,故有3种可能,当第一个元素a确定以后,指针移向第二位置,第二个位置可以和其本身b及其后的元素c进行交换,又可以形成两种排列,当指针指向第三个元素c的时候,这个时候其后没有元素了,此时,则确定了一组排列,输出。但是每次输出后要把数组恢复为原来的样子。
简单来说,它的思想即为,确定第1位,对n-1位进行全排列,确定第二位,对n-2位进行全排列。。。显然,这是一种递归的思想。
def permutations(arr, position, end):
if position == end:
print(arr)
else:
for index in range(position, end):
arr[index], arr[position] = arr[position], arr[index]
permutations(arr, position+1, end)
arr[index], arr[position] = arr[position], arr[index]
arr = ["a","b","c"]
permutations(arr, 0, len(arr))
2.4 LeetCode练习题
2.4.1 有效括号
class Solution(object):
def isValid(self, s):
"""
:type s: str
:rtype: bool
"""
if s is None:
return False
n = len(s)
if n % 2 == 1:
return False
stack = []
left = '([{'
right = ')]}'
lookup = { ')':'(', ']':'[', '}':'{'}
for v in s:
if v in left:
stack.append(v)
if v in right:
if not stack:
return False
p = stack.pop()
if p != lookup[v]:
return False
return stack == []
2.3.2 逆波兰表达式求值
遍历tokens里面的值,对于不是操作符op的项直接加入到栈stack中,当遇到op时,从栈中取出两个进行操作然后将操作后得到的结果再加入到stack里即可,直到遍历结束,返回stack中的值即可
这里需要注意的是,在做除法的时候,题目要求是除了以后返回商的整数部分
class Solution:
def evalRPN(self, tokens):
"""
:type tokens: List[str]
:rtype: int
"""
stack = []
for token in tokens:
if token not in '+-*/':
stack.append(int(token))
else:
r, l = stack.pop(), stack.pop()
if token == '+':
stack.append(r + l)
elif token == '-':
stack.append(l - r)
elif token == '*':
stack.append(r * l)
else:
stack.append(int(l / r))
return stack.pop()
2.4.3 爬楼梯
递归
class Solution(object):
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
if n == 0:
return 0
if n == 1:
return 1
if n == 2:
return 2
return self.climbStairs(n-1) + self.climbStairs(n-2)
循环
class Solution:
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
if n < 3:
return n
dp = [1] * (n+1)
for i in range(2, n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[-1]
2.4.4 滑动窗口最大值
最直观的就是暴力,时间复杂度: O(Nk)
我们可以尝试用队列维护一个大小为k的容器,然后每次求最大值后弹出压入循环做
class Solution(object):
def maxSlidingWindow(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: List[int]
"""
if not nums or len(nums) == 0:
return []
queue = []
res = []
for i in range(k):
queue.append(nums[i])
n = len(nums)
for i in range(k, n):
res.append(max(queue))
queue.pop(0)
queue.append(nums[i])
res.append(max(queue))
return res
3.参考链接
- https://blog.csdn.net/Kaiyuan_sjtu/article/details/88074508
- http://www.xuzhenggen.com/2019/03/03/栈、队列和递归的实现与总结/
- https://blog.csdn.net/qq_31601743/article/details/82053201