利用时间序列ARMA模型和LSTM算法分析并预测pm2.5值

数据来源于 UC Irvine Machine Learning Repository网站中的Beijing PM2.5 Data Data Set，数据文件类型为CSV。

一、利用ARMA模型

数据平稳性分析

还是以天为单位分析这五年之内的pm2.5值，并绘制曲线

ARIMA 模型对时间序列的要求是平稳型，观察图标能看出其没有固定的上升或下降的趋势，粗略判断是平稳序列。不进行差分操作，同时使用ADF单位根平稳型检验，对序列进行平稳性检验。

from statsmodels.tsa.stattools import adfuller as ADF
ADF(test)
#返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore

得到结果如下：

(-18.23039005254537, 2.3680392326349674e-30, 2, 1568, 

{'1%': -3.434527319939446,  '10%': -2.56775226495796,  '5%': -2.863385036059078}, 17309.834345756433)

• 1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的比较，ADF Test result同时小于1%、5%、10%即说明非常好地拒绝该假设.本数据中，adf结果为-18.23， 小于三个level的统计值。
• P-value是否非常接近0.本数据中，P-value 为 2.36e-30,接近0.

ADF检验的原假设是存在单位根，只要这个统计值是小于1%水平下的数字就可以极显著的拒绝原假设，认为数据平稳。

选择合适的ARMA模型

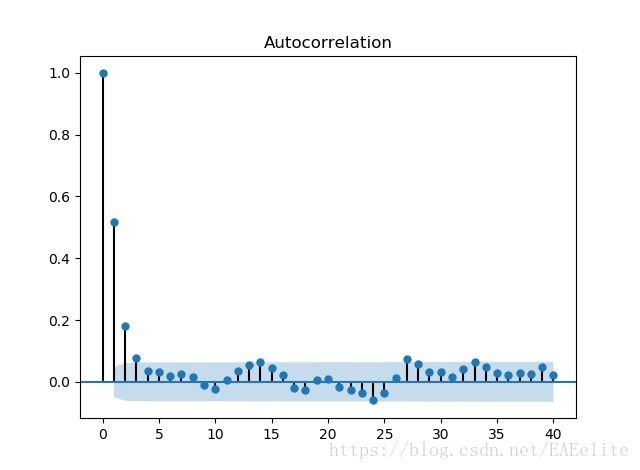
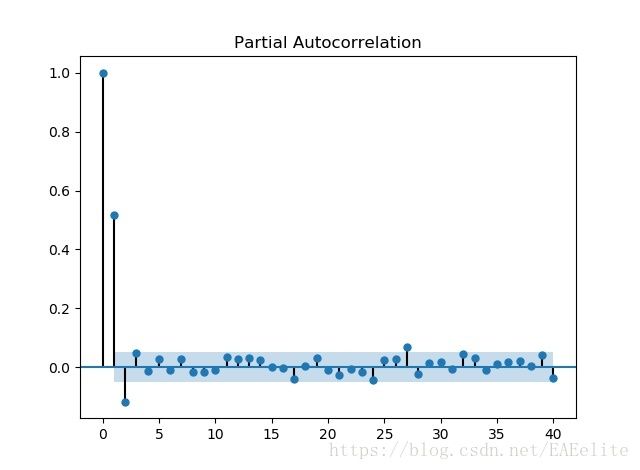
关注序列的自相关图（ACF）和偏自相关图（PACF）

为了避免计算量过大，这里只显示前40阶数据，根据ARMA模型的特征系数选取方法，

可以从ACF和PACF中看出，两图各有3阶在置信区间以外，故选择模型为ARMA（0，3），ARMA（3，0），ARMA（3，3）。

采用ARMA模型的AIC法则，计算三个模型的aic，bic，hqic。
(17593.54679692005, 17620.34413511133, 17603.50667290371)

(17594.582065024613, 17621.37940321589, 17604.541941008272)

(17596.96193511383, 17639.837676219875, 17612.897736687686)

取值最小的模型ARMA（0，3），避免出现过度拟合的情况。

残差分析

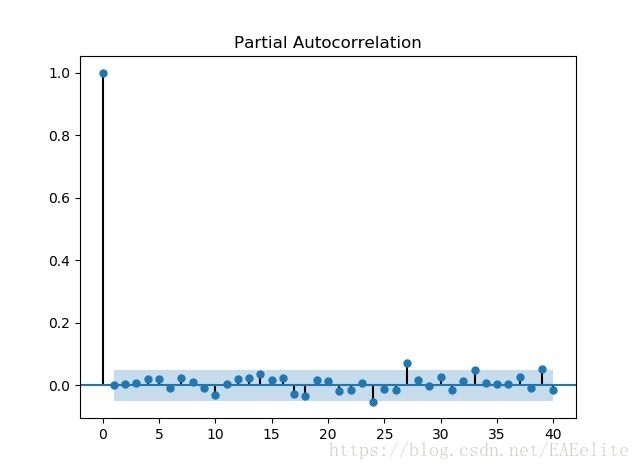
画出ARMA（0，3）模型的ACF和PACF图

可以看出残差属于一阶模型，然后进行德宾-沃森（Durbin-Watson）检验，检验结果是1.9981680279811966，说明残差序列不存在自相关性。

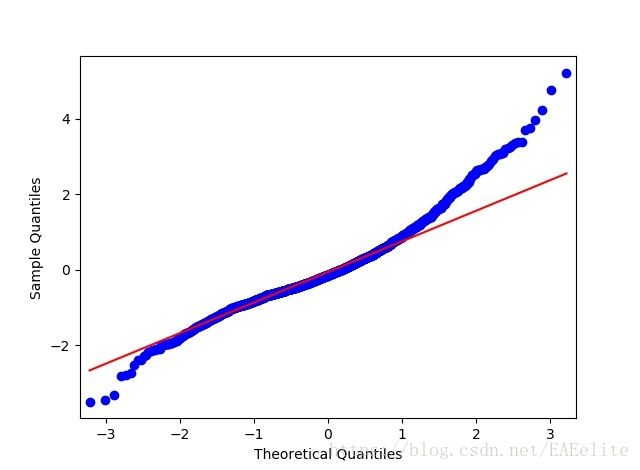
使用QQ图检查残差序列是否服从正态分布，它直观验证一组数据是否来自某个分布，或者验证某两组数据是否来自同一（族）分布。

预测情况

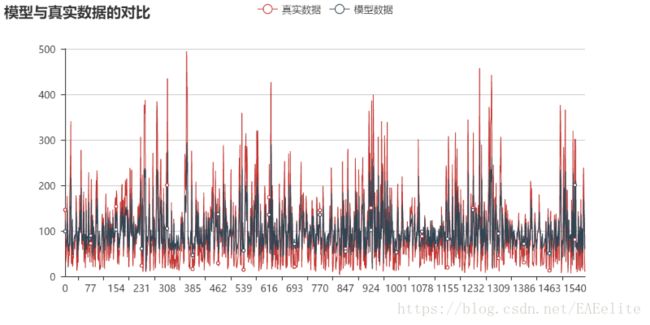
图中是真实数据和模型拟合数据的可视化，其中红色的折线是原始数据的可视化，黑色的折线是模型对红色数据预测的结果的可视化。从图中可以看出，模型基本上模拟出了原始序列的趋势，均方误差为65.19 RMSE。

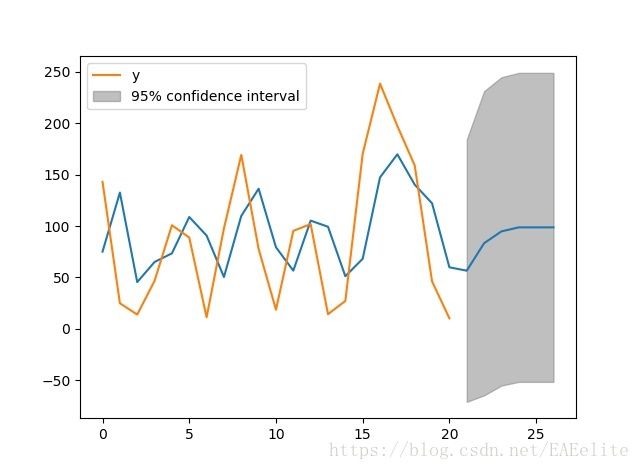
根据模型可以预测出之后几天的pm2.5值

56.50272521, 83.22860983, 94.76099051, 98.68583449, 98.68583449, 98.68583449

二 利用LSTM算法

      LSTM（长短期记忆网络）是RNN的一种变体，RNN与常规神经网络的不同在于层的神经元之间建立起了连接，好处是可以方便的利用序列的前后相关性分析时间序列，但是，RNN由于梯度消失的原因只能有短期记忆，LSTM网络通过精妙的门控制将短期记忆与长期记忆结合起来，并且一定程度上解决了梯度消失的问题，更好的预测序列情况。

数据处理      

       还是利用以天为单位分析这五年之内的pm2.5值，将数据标准化到（0，1）空间内，在原有t时刻单列的基础上，需要增加一列t+1天的数据，因为LSTM是通过时间步幅进行反向传播的，让模型认为当天的数据与前一天有关联。同时按照训练集80%，测试集20%对数据进行划分。

建立 LSTM 模型： 

        输入层有 1 个input，隐藏层有 5 个神经元，输出层就是预测一个值，激活函数用sigmoid，损失函数使用均方误差，优化器用adam，迭代50次，batch size为50。开始训练。

Epoch 47/50
 - 0s - loss: 0.0187 - val_loss: 0.0143
Epoch 48/50
 - 0s - loss: 0.0187 - val_loss: 0.0143
Epoch 49/50
 - 0s - loss: 0.0187 - val_loss: 0.0143
Epoch 50/50
 - 0s - loss: 0.0187 - val_loss: 0.0143

      最后，训练集损失稳定在0.0187，测试集损失为0.0143。训练集Train Score: 67.15 RMSE，测试集Test Score: 58.75 RMSE。损失曲线如下图所示。

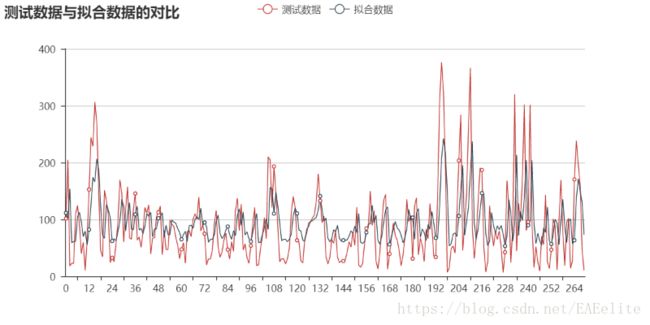
        训练集和测试集的原始数据与拟合数据如下图所示。

 

总结

      本文主要介绍时间序列ARMA相关模型的建立及诊断和预测过程。文章首先使用pandas读入数据、整理数据；然后使用statsmodels库对原始数据序列进行平稳性检验；之后通过ACF和PACF图对模型参数进行初步确定，之后使用statsmodels库中相关的时间序列函数进行时间序列模型ARMA的识别，拟合模型，对拟合前后的数据进行对比分析；对ARMA(0，3)模型进行模型的诊断，主要包括自相关性检验；基于此我们接着使用ARMA(0，3)模型对数据进行了预测；最后，我们预测得到之后6天的预测结果，至此完成了整个时间序列模型的全流程建模过程。

        另外，利用LSTM算法也对该时间序列进行了拟合研究，发现两者的拟合均方误差基本相同，说明两种方法的拟合效果基本一致。

 

参考文章：

https://blog.csdn.net/kicilove/article/details/78321405

https://blog.csdn.net/aspirinvagrant/article/details/46323271

http://www.cnblogs.com/taojake-ML/p/6400858.html

https://blog.csdn.net/kunlong0909/article/details/52756821

http://www.statsmodels.org/stable/examples/notebooks/generated/tsa_arma_0.html

https://yq.aliyun.com/articles/174270?utm_content=m_28754#comment

https://blog.csdn.net/aliceyangxi1987/article/details/73420583