经典算法问题-01-八皇后
#八皇后问题
###问题描述:
八皇后问题,是一个古老而著名的问题,是回溯算法的典型案例。在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
###简化问题:
由于八皇后问题的正确答案为92种排列方案,由于正确的棋子放置方式实在太多,难以一一列举,所以先简化问题,解决四皇后的排列,即将8×8棋局改为4×4棋局,规则不变
###建立模型:
要使用C++解决这个问题,首先要建立模型,让问题能够使用数学和C++的控制语句来解决。
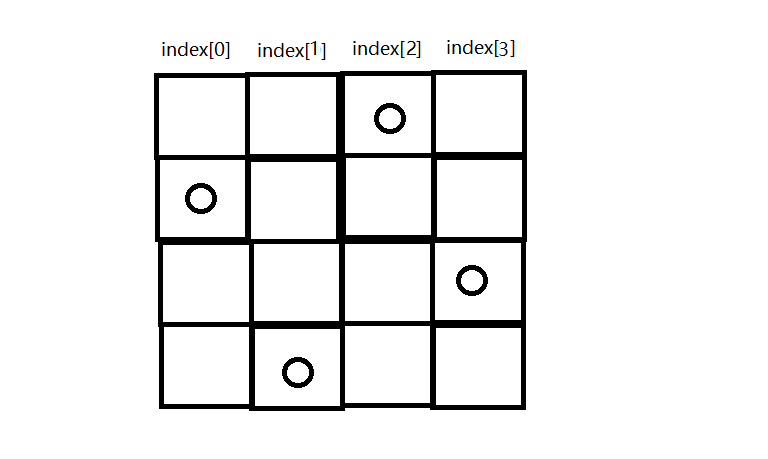
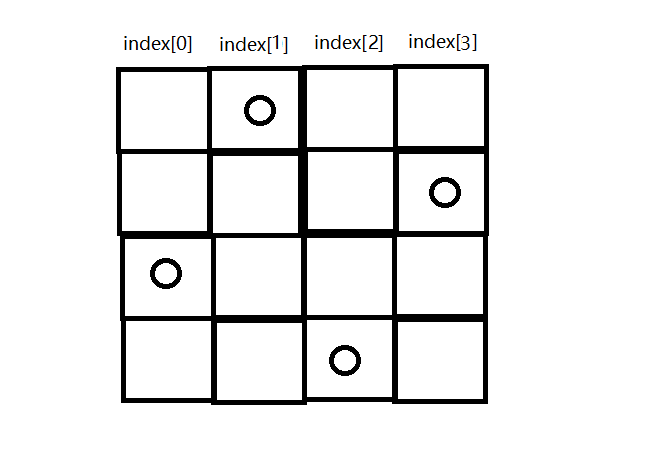
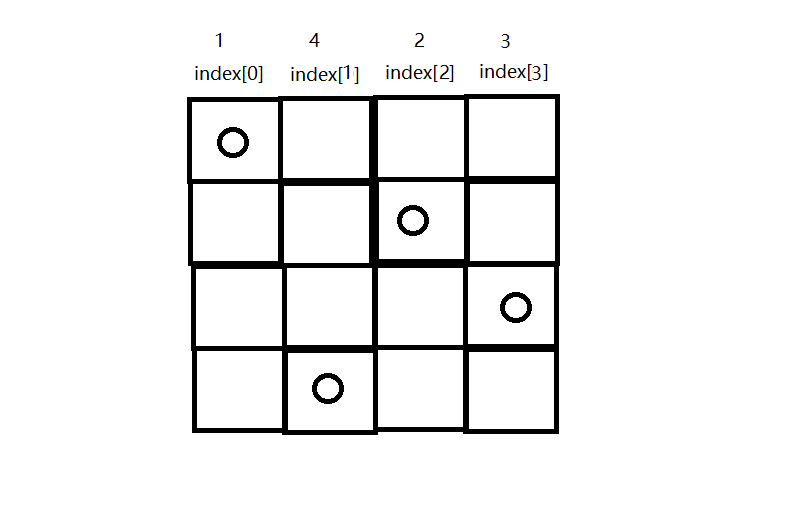
将棋盘模拟为一个坐标轴,使用一个数组index将每个棋子定位到坐标轴中,index数组的下标为横坐标值,index[i]的值为纵坐标值,如下图所示,index[0] = 1 ; index[1] = 4 ; index[2] = 2 ; index[3] = 3
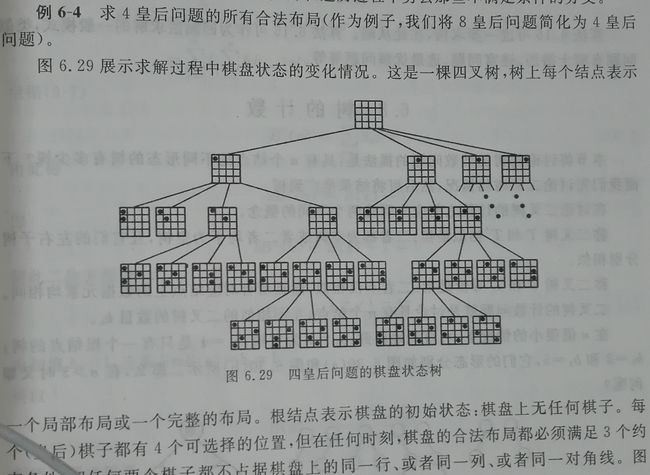
#方案1----枚举法:
将所有可能的棋子放置情况全部列举出来,一一判断是否合乎条件
###C++程序:
#include
using namespace std;
//判断棋子放置方式是否正确
bool Judge(int *index) {
for (int i = 0; i < 4; i++){
for (int j = i + 1 ; j < 4; j++) {
//判断棋子是否在同一行,或某一对角线上
//1,横坐标不同 i与j不相等
//2,纵坐标不同 index[i]与index[j]不相等
//3,不在同一对角线 index[i]- index[j]的绝对值和j-i的绝对值不相等
if (index[i] == index[j] || abs(index[i]- index[j])==j-i){
return false;
}
}
}
return true;
}
//打印正确的棋子放置方式
void Sloution(int *index) {
cout << "四皇后问题的一种正确解法,横坐标从0到4的4列上,纵坐标的值依次是:";
for (int i = 0; i < 4; i++){
cout << index[i];
}
cout << endl;
}
int main() {
int index[8];
//多层循环,穷举每一种放置方式
for (index[0] = 1; index[0] <= 4 ; index[0]++){
for (index[1] = 1; index[1] <= 4; index[1]++) {
for (index[2] = 1; index[2] <= 4; index[2]++) {
for (index[3] = 1; index[3] <= 4; index[3]++) {
//判断棋子放置是否合乎规则,正确则打印,不正确则继续
if (Judge(index)){
Sloution(index);
}
else {
continue;
}
}
}
}
}
cin.get();
return 0;
}
上述程序使用了4个for循环来模拟所有可能出现的棋子放置情况,Judge()方法用来判断是否合乎条件
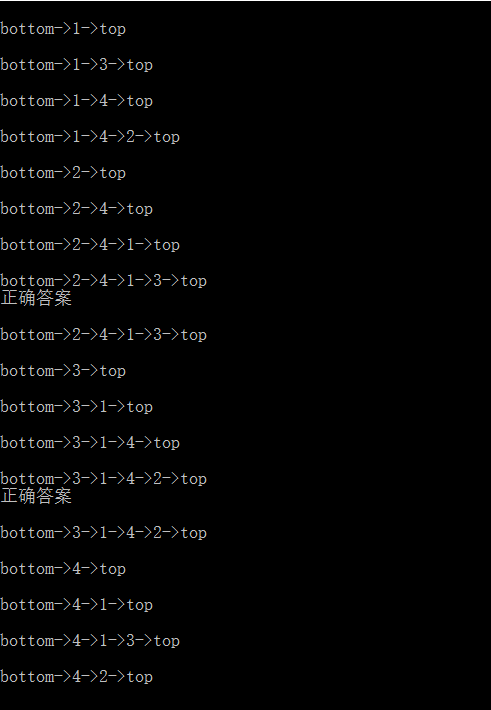
###运行结果:
###正确结果的演示:
纵坐标:2413
纵坐标:3142
##枚举法的优化:
枚举法解决此四皇后问题需要的循环次数太多,四皇后需要4X4X4X4次遍历,才能将所有可能的情况列举出来,八皇后更是要8X8X8X8X8X8X8X8次遍历
枚举法可以进行优化,即若在放置第2,或3个棋子,即没有将棋子全部放入棋盘中时,进行判断,将不符合要求的情况直接排除,不再继续循环,这样能够大大减少循环次数,不必模拟所有棋子放置方式
优化方式:在main方法中做优化,增加判断语句
int main() {
int index[8];
//多层循环,穷举每一种放置方式
for (index[0] = 1; index[0] <= 4; index[0]++) {
for (index[1] = 1; index[1] <= 4; index[1]++) {
//增加判断
if(Judge(index, 2))
for (index[2] = 1; index[2] <= 4; index[2]++) {
//增加判断
if (Judge(index, 3))
for (index[3] = 1; index[3] <= 4; index[3]++) {
//判断棋子放置是否合乎规则,正确则打印,不正确则继续
if (Judge(index, 4)) {
Sloution(index);
}
else {
continue;
}
}
}
}
}
cin.get();
return 0;
}
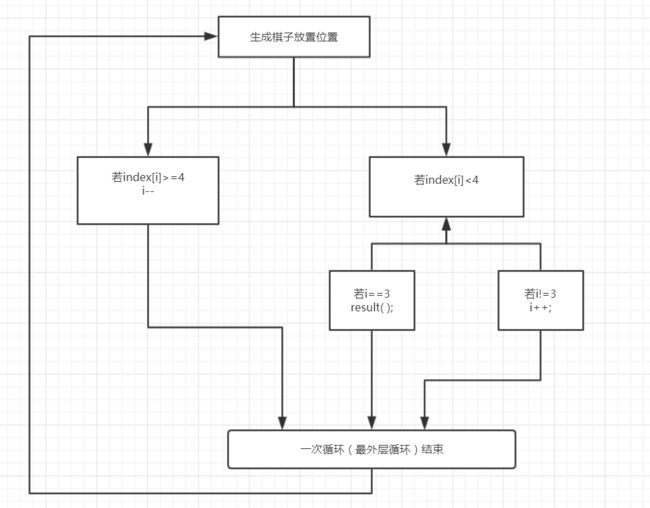
#方案2----回溯法:
main函数:
int main() {
int index[4] = { 0 };
int i = 0;
while (i > -1) {
index[i]++;
while (index[i] < 6 && _judge(index, i)) {
index[i]++;
}
if (index[i] <= 4) {
if (i == 3) {
//是四皇后的正确结果,调用函数打印正确答案
result(index);
}
else {
i++;
index[i] = 0;
}
}
else {
i--;
}
}
cin.get();
return 0;
}
_judge函数:
inline bool _judge(int *index, int num) {
for (int i = 0; i < num; i++) {
if (index[i] == index[num] || abs(index[i] - index[num]) == num - i) {
return true;
}
}
return false;
}
result函数:
inline void result(int *index) {
cout << "四皇后问题的一种正确解法,横坐标从0到4的4列上,纵坐标的值依次是:";
for (int i = 0; i < 4; i++) {
cout << index[i];
}
cout << endl;
}
##使用递归优化程序:
上述程序太难懂,可以使用递归优化上述程序,如下:
result函数和_judge函数不变
回调函数:
void callback(int *index,int i) {
if (i > 3){
result(index);
}
else{
int j = 0;
while (++j <= 4) {
index[i] = j;
if (_judge(index, i) == 0) {
callback(index,i+1);
}
}
}
}
main函数:
int main() {
int index[4] = { 0,0,0,0 };
int i = 0;
callback(index,i);
cin.get();
return 0;
}
#方案3----回溯法结合递归和栈数据结构
在严蔚敏编著的C语言数据结构栈数据结构部分,书中提及使用栈解决四皇后问题
栈数据结构解决和回溯相关的问题时非常的方便易懂,下面介绍一下使用栈解决四皇后问题,这是本文最简单易懂的方法,但是需要实现编写栈数据结构,当然也可以使用STL中的栈
#include "assist.h"
#include"Stack.h"
#include
//创建一个全局栈
Stack stack(11);
//回调函数
void callback() {
if (stack.getSize() == 3) {
cout << "正确答案" << endl;
stack.Print();
}
else {
int j = 0;
while (++j <= 4)
{
//进栈
stack.Push(j);
if (_judge( stack.getElements(), stack.getSize()) == 0) {
//打印整个栈中的数据
stack.Print();
cout << stack.getSize() << endl;
callback();
}
//弹栈
stack.Pop();
}
}
}
int main() {
callback();
cin.get();
return 0;
}