【Python数据挖掘课程】二.Kmeans聚类数据分析及Anaconda介绍
主要内容包括:
1.Anaconda软件的安装过程及简单配置
2.聚类及Kmeans算法介绍
3.案例分析:Kmeans实现运动员位置聚集
前文推荐:【Python数据挖掘课程】一.安装Python及爬虫入门介绍
希望这篇文章对你有所帮助,尤其是刚刚接触数据挖掘以及大数据的同学,同时准备尝试以案例为主的方式进行讲解。如果文章中存在不足或错误的地方,还请海涵~
一. Anaconda软件安装及使用步骤
前面两节课我是通过Python命令行和IDLE工具进行介绍的,但是里面的配置比较麻烦,包括pip安装,selenium、lda各种第三方包的安装。
从这节课我准备使用Anacaonda软件来讲解,它集成了各种Python的第三方包,尤其包括数据挖掘和数据分析常用的几个包。
下载地址:https://www.continuum.io/downloads/
云盘分享:http://pan.baidu.com/s/1hrEQ9xi
1. 配置过程
首先简单介绍安装过程以及如何使用。
安装Anaconda
安装过程如下所示:
安装最好在C盘默认路径下(空间不大,方便配置),同时不要使用中文路径。
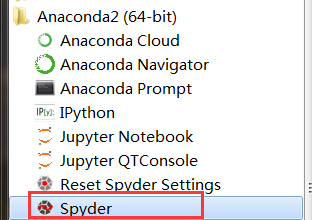
安装完成后,点击“Finish”。点击Anaconda文件夹,包括这些exe执行文件:
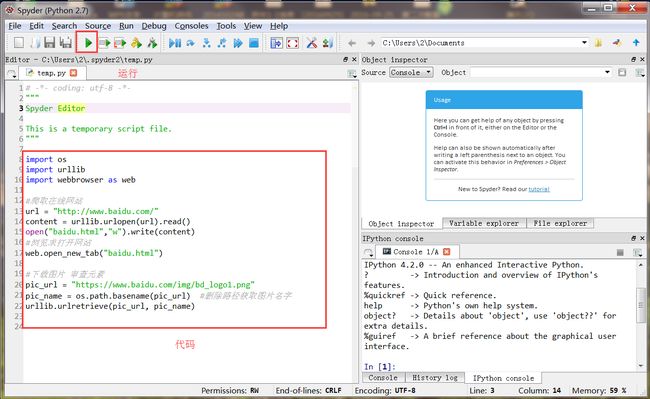
这里我们使用Spyder进行编写Python程序。运行如下所示,左边是进行代码编写的,右下角Console是输出结果的地方。
安装第三方包
虽然Anaconda软件集成了各种各样的包,但是还是缺少一些第三方包,需要通过调用pip或easy_install命令进行安装。
然后使用cd ..去到C盘根目录,cd去到Anaconda的Scripts目录下,输入"pip install selenium"安装selenium相应的包,"pip install lda"安装lda包。
推荐文章:Windows下Anaconda的安装和简单使用 - yido2. 机器学习常用包
下面这四个包通常用于Python数据挖掘和大数据分析的,包括:
Scikit-Learn
Scikit-Learn是一个基于python的用于数据挖掘和数据分析的简单且有效的工具,它的基本功能主要被分为六个部分:分类(Classification)、回归(Regression)、聚类(Clustering)、数据降维(Dimensionality Reduction)、模型选择(Model Selection)、数据预处理(Preprocessing)。
详见官网:http://scikit-learn.org/stable/
NumPy
NumPy(Numeric Python)系统是Python的一种开源的数值计算扩展,一个用python实现的科学计算包。它提供了许多高级的数值编程工具,如:矩阵数据类型、矢量处理,以及精密的运算库。专为进行严格的数字处理而产生。
SciPy
SciPy (pronounced "Sigh Pie") 是一个开源的数学、科学和工程计算包。它是一款方便、易于使用、专为科学和工程设计的Python工具包,包括统计、优化、整合、线性代数模块、傅里叶变换、信号和图像处理、常微分方程求解器等等。
Matplotlib
Matplotlib是一个Python的图形框架,类似于MATLAB和R语言。它是python最著名的绘图库,它提供了一整套和matlab相似的命令API,十分适合交互式地进行制图。而且也可以方便地将它作为绘图控件,嵌入GUI应用程序中。
二. 聚类及Kmeans介绍
这部分内容主要简单介绍聚类的原理及Kmeans相关知识。
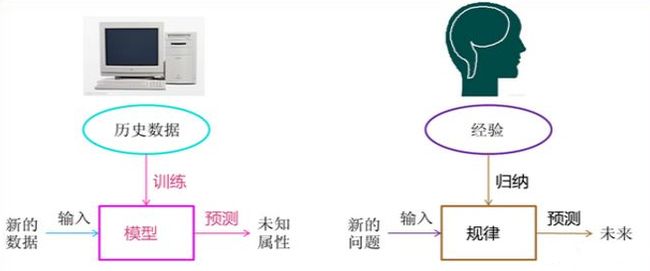
机器学习的基本思想,我还是介绍下面这张图,非常经典。
这里讲述聚类的部分,我简单推荐"简书-程sir"的文章,简单易懂,很不错。
推荐地址:http://www.jianshu.com/p/fc91fed8c77b
1. 分类与聚类
聚类
俗话说“物以类聚”,其实从广义上说,聚类就是将数据集中在某些方面相似的数据成员放在一起。一个聚类就是一些数据实例的集合,其中处于相同聚类中的数据元素彼此相似,但是处于不同聚类中的元素彼此不同。
由于在聚类中那些表示数据类别的分类或分组信息是没有的,即这些数据是没有标签的,所有聚类及时通常被成为无监督学习(Unsupervised Learning)。
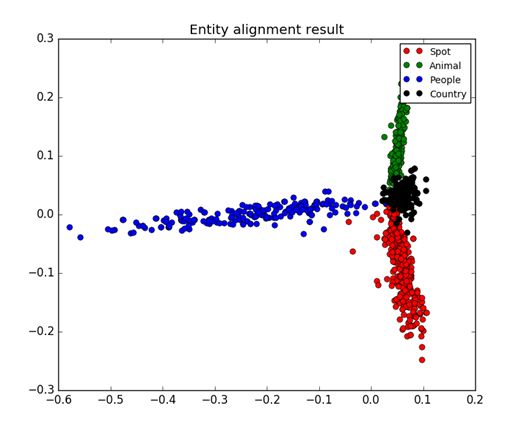
下图是800篇文章,每个点可以看成一篇文章,然后对文本进行聚类分析,可以看到相同主题的文章是聚集在一起的。总共四个主题,红色表示景区Spot、蓝色表示人物People、黑色表示国家Country、绿色表示动物Animal。
分类
在理解聚类之前,必须要先理解聚类和分类的区别,简单举个例子。
分类其实是从特定的数据中挖掘模式,作出判断的过程。比如Gmail邮箱里有垃圾邮件分类器,一开始的时候可能什么都不过滤,在日常使用过程中,我人工对于每一封邮件点选“垃圾”或“不是垃圾”,过一段时间,Gmail就体现出一定的智能,能够自动过滤掉一些垃圾邮件了。
这是因为在点选的过程中,其实是给每一条邮件打了一个“标签”,这个标签只有两个值,要么是“垃圾”,要么“不是垃圾”,Gmail就会不断研究哪些特点的邮件是垃圾,哪些特点的不是垃圾,形成一些判别的模式,这样当一封信的邮件到来,就可以自动把邮件分到“垃圾”和“不是垃圾”这两个我们人工设定的分类的其中一个。
(1)训练数据集存在一个类标记号,判断它是正向数据集(起积极作用,不垃圾邮件),还是负向数据集(起抑制作用,垃圾邮件);
(2)然后需要对数据集进行学习训练,并构建一个训练的模型;
(3)通过该模型对预测数据集进预测,并计算其结果的性能。
聚类的的目的也是把数据分类,但是事先我是不知道如何去分的,完全是算法自己来判断各条数据之间的相似性,相似的就放在一起。在聚类的结论出来之前,我完全不知道每一类有什么特点,一定要根据聚类的结果通过人的经验来分析,看看聚成的这一类大概有什么特点。
总之,聚类主要是"物以类聚",通过相似性把相似元素聚集在一起,它没有标签;而分类通过标签来训练得到一个模型,对新数据集进行预测的过程,其数据存在标签的。
2. Kmeans算法
该部分转载简书-程sir的文章:聚类、K-Means、例子、细节
K-Means是聚类算法中的最常用的一种,算法最大的特点是简单,好理解,运算速度快,但是只能应用于连续型的数据,并且一定要在聚类前需要手工指定要分成几类。
下面,我们描述一下K-means算法的过程,为了尽量不用数学符号,所以描述的不是很严谨,大概就是这个意思,“物以类聚、人以群分”:
1、首先输入k的值,即我们希望将数据集经过聚类得到k个分组。
2、从数据集中随机选择k个数据点作为初始大哥(质心,Centroid)
3、对集合中每一个小弟,计算与每一个大哥的距离(距离的含义后面会讲),离哪个大哥距离近,就跟定哪个大哥。
4、这时每一个大哥手下都聚集了一票小弟,这时候召开人民代表大会,每一群选出新的大哥(其实是通过算法选出新的质心)。
5、如果新大哥和老大哥之间的距离小于某一个设置的阈值(表示重新计算的质心的位置变化不大,趋于稳定,或者说收敛),可以认为我们进行的聚类已经达到期望的结果,算法终止。
6、如果新大哥和老大哥距离变化很大,需要迭代3~5步骤。
下面这个例子很好的,真心推荐大家学习他的博客。
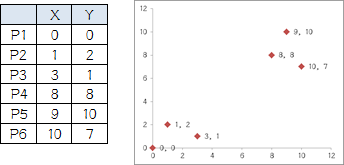
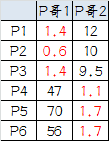
他搞了6个点,从图上看应该分成两推儿,前三个点一堆儿,后三个点是另一堆儿。现在手工执行K-Means,体会一下过程,同时看看结果是不是和预期一致。
1.选择初始大哥:
我们就选P1和P2
2.计算小弟和大哥的距离:
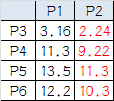
P3到P1的距离从图上也能看出来(勾股定理),是√10 = 3.16;P3到P2的距离√((3-1)^2+(1-2)^2 = √5 = 2.24,所以P3离P2更近,P3就跟P2混。同理,P4、P5、P6也这么算,如下:
P3到P6都跟P2更近,所以第一次站队的结果是:
• 组A:P1
• 组B:P2、P3、P4、P5、P6
3.人民代表大会:
组A没啥可选的,大哥还是P1自己
组B有五个人,需要选新大哥,这里要注意选大哥的方法是每个人X坐标的平均值和Y坐标的平均值组成的新的点,为新大哥,也就是说这个大哥是“虚拟的”。
因此,B组选出新大哥的坐标为:P哥((1+3+8+9+10)/5,(2+1+8+10+7)/5)=(6.2,5.6)。
综合两组,新大哥为P1(0,0),P哥(6.2,5.6),而P2-P6重新成为小弟。
4.再次计算小弟到大哥的距离:
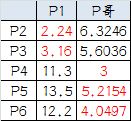
这时可以看到P2、P3离P1更近,P4、P5、P6离P哥更近,第二次站队的结果是:
• 组A:P1、P2、P3
• 组B:P4、P5、P6(虚拟大哥这时候消失)
5.第二届人民代表大会:
按照上一届大会的方法选出两个新的虚拟大哥:P哥1(1.33,1) P哥2(9,8.33),P1-P6都成为小弟。
6.第三次计算小弟到大哥的距离:
这时可以看到P1、P2、P3离P哥1更近,P4、P5、P6离P哥2更近,所以第二次站队的结果是:
• 组A:P1、P2、P3
• 组B:P4、P5、P6
我们发现,这次站队的结果和上次没有任何变化了,说明已经收敛,聚类结束,聚类结果和我们最开始设想的结果完全一致。
三. 案例分析:Kmeans聚类运动员数据
1. 数据集
现在存在下面的数据集,是篮球球员比赛的数据。
数据集地址:KEEL-dataset - Basketball data set
该数据集主要包括5个特征(Features),共96行数据。
特征描述:共5个特征,每分钟助攻数、运动员身高、运动员出场时间、运动员年龄和每分钟得分数。
20行数据集如下:
assists_per_minute height time_played age points_per_minute
0 0.0888 201 36.02 28 0.5885
1 0.1399 198 39.32 30 0.8291
2 0.0747 198 38.80 26 0.4974
3 0.0983 191 40.71 30 0.5772
4 0.1276 196 38.40 28 0.5703
5 0.1671 201 34.10 31 0.5835
6 0.1906 193 36.20 30 0.5276
7 0.1061 191 36.75 27 0.5523
8 0.2446 185 38.43 29 0.4007
9 0.1670 203 33.54 24 0.4770
10 0.2485 188 35.01 27 0.4313
11 0.1227 198 36.67 29 0.4909
12 0.1240 185 33.88 24 0.5668
13 0.1461 191 35.59 30 0.5113
14 0.2315 191 38.01 28 0.3788
15 0.0494 193 32.38 32 0.5590
16 0.1107 196 35.22 25 0.4799
17 0.2521 183 31.73 29 0.5735
18 0.1007 193 28.81 34 0.6318
19 0.1067 196 35.60 23 0.4326
20 0.1956 188 35.28 32 0.4280 需求:现在需要通过运动员的数据,判断他是什么位置。
如果某些运动员得分高,他可能是得分后卫;如果某些运动员身高高或篮板多,他可能是中锋;助攻高可能是控卫。
2. 代码
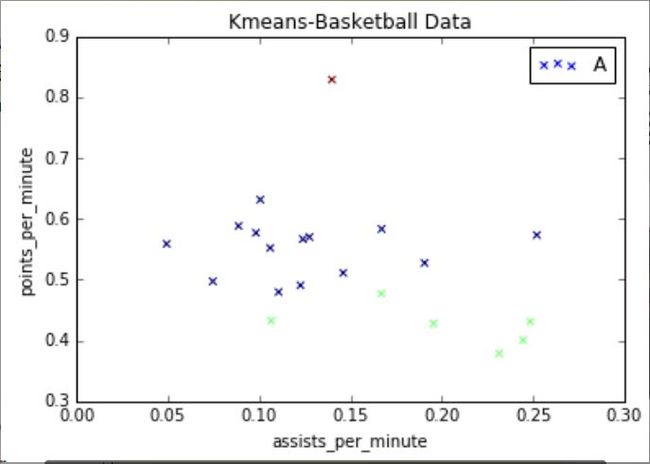
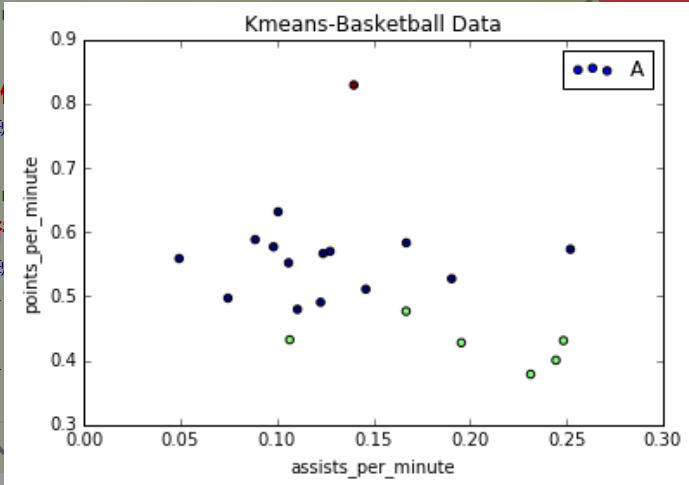
这里我仅仅使用两列数据,助攻数和得分数进行实验,相当于20*2的矩阵,其中输出y_pred结果表示聚类的类标。类簇数设置为3,类标位0、1、2,它也是与20个球员数据一一对应的。
Sklearn机器学习包中导入了KMeans聚类,同时需要注意Matplotlib包绘制图形的过程。代码如下,并包括详细注释:
"""
第一部分:导入包
从sklearn.cluster机器学习聚类包中导入KMeans聚类
"""
# coding=utf-8
from sklearn.cluster import Birch
from sklearn.cluster import KMeans
"""
第二部分:数据集
X表示二维矩阵数据,篮球运动员比赛数据
总共20行,每行两列数据
第一列表示球员每分钟助攻数:assists_per_minute
第二列表示球员每分钟得分数:points_per_minute
"""
X = [[0.0888, 0.5885],
[0.1399, 0.8291],
[0.0747, 0.4974],
[0.0983, 0.5772],
[0.1276, 0.5703],
[0.1671, 0.5835],
[0.1906, 0.5276],
[0.1061, 0.5523],
[0.2446, 0.4007],
[0.1670, 0.4770],
[0.2485, 0.4313],
[0.1227, 0.4909],
[0.1240, 0.5668],
[0.1461, 0.5113],
[0.2315, 0.3788],
[0.0494, 0.5590],
[0.1107, 0.4799],
[0.2521, 0.5735],
[0.1007, 0.6318],
[0.1067, 0.4326],
[0.1956, 0.4280]
]
#输出数据集
print X
"""
第三部分:KMeans聚类
clf = KMeans(n_clusters=3) 表示类簇数为3,聚成3类数据,clf即赋值为KMeans
y_pred = clf.fit_predict(X) 载入数据集X,并且将聚类的结果赋值给y_pred
"""
clf = KMeans(n_clusters=3)
y_pred = clf.fit_predict(X)
#输出完整Kmeans函数,包括很多省略参数
print(clf)
#输出聚类预测结果,20行数据,每个y_pred对应X一行或一个球员,聚成3类,类标为0、1、2
print(y_pred)
"""
第四部分:可视化绘图
Python导入Matplotlib包,专门用于绘图
import matplotlib.pyplot as plt 此处as相当于重命名,plt用于显示图像
"""
import numpy as np
import matplotlib.pyplot as plt
#获取第一列和第二列数据 使用for循环获取 n[0]表示X第一列
x = [n[0] for n in X]
print x
y = [n[1] for n in X]
print y
#绘制散点图 参数:x横轴 y纵轴 c=y_pred聚类预测结果 marker类型 o表示圆点 *表示星型 x表示点
plt.scatter(x, y, c=y_pred, marker='x')
#绘制标题
plt.title("Kmeans-Basketball Data")
#绘制x轴和y轴坐标
plt.xlabel("assists_per_minute")
plt.ylabel("points_per_minute")
#设置右上角图例
plt.legend(["A","B","C"])
#显示图形
plt.show()
聚类核心代码:
from sklearn.cluster import KMeans
clf = KMeans(n_clusters=3)
y_pred = clf.fit_predict(X)
绘图核心代码:
import matplotlib.pyplot as plt
plt.scatter(x, y, c=y_pred, marker='x')
plt.title("Kmeans-Basketball Data")
plt.xlabel("assists_per_minute")
plt.ylabel("points_per_minute")
plt.show()
3. 运行结果
运行结果如下所示:
#数据集
[[0.0888, 0.5885], [0.1399, 0.8291], [0.0747, 0.4974], [0.0983, 0.5772], [0.1276, 0.5703], [0.1671, 0.5835], [0.1906, 0.5276], [0.1061, 0.5523], [0.2446, 0.4007], [0.167, 0.477], [0.2485, 0.4313], [0.1227, 0.4909], [0.124, 0.5668], [0.1461, 0.5113], [0.2315, 0.3788], [0.0494, 0.559], [0.1107, 0.4799], [0.2521, 0.5735], [0.1007, 0.6318], [0.1067, 0.4326], [0.1956, 0.428]]
#KMeans函数
KMeans(copy_x=True, init='k-means++', max_iter=300, n_clusters=3, n_init=10,
n_jobs=1, precompute_distances='auto', random_state=None, tol=0.0001,
verbose=0)
#y_pred 预测的聚类类标结果
[0 2 0 0 0 0 0 0 1 1 1 0 0 0 1 0 0 0 0 1 1]
#获取x、y坐标
[0.0888, 0.1399, 0.0747, 0.0983, 0.1276, 0.1671, 0.1906, 0.1061, 0.2446, 0.167, 0.2485, 0.1227, 0.124, 0.1461, 0.2315, 0.0494, 0.1107, 0.2521, 0.1007, 0.1067, 0.1956]
[0.5885, 0.8291, 0.4974, 0.5772, 0.5703, 0.5835, 0.5276, 0.5523, 0.4007, 0.477, 0.4313, 0.4909, 0.5668, 0.5113, 0.3788, 0.559, 0.4799, 0.5735, 0.6318, 0.4326, 0.428] 如果设置marker='o',输出圆形,可以看到红色点很高,他得分和助攻都比较高,相当于篮球里面的"乔丹",然后中间一部分,右下角一部分助攻很高、得分低,可能是控卫。当然数据集越多,聚类的效果越好。
常见问题:
1、安装Anaconda不能使用中文路径,以及电脑名称为中文;
2、Spyder如何显示中文,而不是"口口口"乱码,需要改Fonts;
3、Matplotlib如何显示颜色,定义样式等;
4、如何读取数据,赋值给变量,在让其显示。
希望这篇文章对你有所帮助,主要是介绍一个基于Python的Kmeans聚类案例,后面会陆续详细介绍各种知识。非常想上好这门课,因为是我的专业方向,另外学生们真的好棒,好认真,用手机录像、问问题、配环境等等,只要有用心的学生,我定不负你!同时,这节课的思路好点了,摸着石头过马路,需要慢慢学吧,但还是挺享受的,毕竟9800,哈哈哈!
(By:Eastmount 2016-10-10 晚上10点 http://blog.csdn.net/eastmount/ )
最后提供篮球的完整数据集:
@relation basketball
@attribute assists_per_minuteReal real [0.0494, 0.3437]
@attribute heightInteger integer [160, 203]
@attribute time_playedReal real [10.08, 40.71]
@attribute ageInteger integer [22, 37]
@attribute points_per_minuteReal real [0.1593, 0.8291]
@inputs assists_per_minuteReal, heightInteger, time_playedReal, ageInteger, points_per_minuteReal
@data
0.0888, 201, 36.02, 28, 0.5885
0.1399, 198, 39.32, 30, 0.8291
0.0747, 198, 38.8, 26, 0.4974
0.0983, 191, 40.71, 30, 0.5772
0.1276, 196, 38.4, 28, 0.5703
0.1671, 201, 34.1, 31, 0.5835
0.1906, 193, 36.2, 30, 0.5276
0.1061, 191, 36.75, 27, 0.5523
0.2446, 185, 38.43, 29, 0.4007
0.167, 203, 33.54, 24, 0.477
0.2485, 188, 35.01, 27, 0.4313
0.1227, 198, 36.67, 29, 0.4909
0.124, 185, 33.88, 24, 0.5668
0.1461, 191, 35.59, 30, 0.5113
0.2315, 191, 38.01, 28, 0.3788
0.0494, 193, 32.38, 32, 0.559
0.1107, 196, 35.22, 25, 0.4799
0.2521, 183, 31.73, 29, 0.5735
0.1007, 193, 28.81, 34, 0.6318
0.1067, 196, 35.6, 23, 0.4326
0.1956, 188, 35.28, 32, 0.428
0.1828, 191, 29.54, 28, 0.4401
0.1627, 196, 31.35, 28, 0.5581
0.1403, 198, 33.5, 23, 0.4866
0.1563, 193, 34.56, 32, 0.5267
0.2681, 183, 39.53, 27, 0.5439
0.1236, 196, 26.7, 34, 0.4419
0.13, 188, 30.77, 26, 0.3998
0.0896, 198, 25.67, 30, 0.4325
0.2071, 178, 36.22, 30, 0.4086
0.2244, 185, 36.55, 23, 0.4624
0.3437, 185, 34.91, 31, 0.4325
0.1058, 191, 28.35, 28, 0.4903
0.2326, 185, 33.53, 27, 0.4802
0.1577, 193, 31.07, 25, 0.4345
0.2327, 185, 36.52, 32, 0.4819
0.1256, 196, 27.87, 29, 0.6244
0.107, 198, 24.31, 34, 0.3991
0.1343, 193, 31.26, 28, 0.4414
0.0586, 196, 22.18, 23, 0.4013
0.2383, 185, 35.25, 26, 0.3801
0.1006, 198, 22.87, 30, 0.3498
0.2164, 193, 24.49, 32, 0.3185
0.1485, 198, 23.57, 27, 0.3097
0.227, 191, 31.72, 27, 0.4319
0.1649, 188, 27.9, 25, 0.3799
0.1188, 191, 22.74, 24, 0.4091
0.194, 193, 20.62, 27, 0.3588
0.2495, 185, 30.46, 25, 0.4727
0.2378, 185, 32.38, 27, 0.3212
0.1592, 191, 25.75, 31, 0.3418
0.2069, 170, 33.84, 30, 0.4285
0.2084, 185, 27.83, 25, 0.3917
0.0877, 193, 21.67, 26, 0.5769
0.101, 193, 21.79, 24, 0.4773
0.0942, 201, 20.17, 26, 0.4512
0.055, 193, 29.07, 31, 0.3096
0.1071, 196, 24.28, 24, 0.3089
0.0728, 193, 19.24, 27, 0.4573
0.2771, 180, 27.07, 28, 0.3214
0.0528, 196, 18.95, 22, 0.5437
0.213, 188, 21.59, 30, 0.4121
0.1356, 193, 13.27, 31, 0.2185
0.1043, 196, 16.3, 23, 0.3313
0.113, 191, 23.01, 25, 0.3302
0.1477, 196, 20.31, 31, 0.4677
0.1317, 188, 17.46, 33, 0.2406
0.2187, 191, 21.95, 28, 0.3007
0.2127, 188, 14.57, 37, 0.2471
0.2547, 160, 34.55, 28, 0.2894
0.1591, 191, 22.0, 24, 0.3682
0.0898, 196, 13.37, 34, 0.389
0.2146, 188, 20.51, 24, 0.512
0.1871, 183, 19.78, 28, 0.4449
0.1528, 191, 16.36, 33, 0.4035
0.156, 191, 16.03, 23, 0.2683
0.2348, 188, 24.27, 26, 0.2719
0.1623, 180, 18.49, 28, 0.3408
0.1239, 180, 17.76, 26, 0.4393
0.2178, 185, 13.31, 25, 0.3004
0.1608, 185, 17.41, 26, 0.3503
0.0805, 193, 13.67, 25, 0.4388
0.1776, 193, 17.46, 27, 0.2578
0.1668, 185, 14.38, 35, 0.2989
0.1072, 188, 12.12, 31, 0.4455
0.1821, 185, 12.63, 25, 0.3087
0.188, 180, 12.24, 30, 0.3678
0.1167, 196, 12.0, 24, 0.3667
0.2617, 185, 24.46, 27, 0.3189
0.1994, 188, 20.06, 27, 0.4187
0.1706, 170, 17.0, 25, 0.5059
0.1554, 183, 11.58, 24, 0.3195
0.2282, 185, 10.08, 24, 0.2381
0.1778, 185, 18.56, 23, 0.2802
0.1863, 185, 11.81, 23, 0.381
0.1014, 193, 13.81, 32, 0.1593