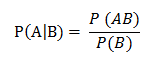朴素贝叶斯
概念:
英文名Naive Bayesian Model,简称NB,是一种玩条件概率的分类模型。
条件概率公式:
P(A) 指事件A发生的概率;
P(AB) 指事件A与B同时发生的概率;
P(A|B) 指事件A在事件B已经发生的情况下,发生的概率。
示例:
评价分类,好评(标记为0)或差评(标记为1)的数据集 DataSet:
上面的单词模型 VacbModel(词袋模型)就是:
[my, problems, cute, dalmation, so, licks, steak, take, food, stupid, I, posting, ate, not, quit, has, maybe, flea, dog, him, please, garbage, buying, to, worthless, love, is, stop, mr, how, park, help] 32项
DataSet[0] 中的 problems 对应到 VacbModel 中的第2项,也即 VacbModel[1]。如果对应到即表示1,没有对应就表示为0,那么DataSet[0]的词集是:
[1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0,1,1,0,1,0,0,0,0,0,0,0,0,0,0,1]
设A为 “一个句子出现这些词”,设B为“分类结果”,如果要求某个句子是好评还是差评,那么要求的就是P(AB),P(A)是抽象的,但P(B)是好求的,那么问题就是P(A|B)。
可以从这个角度想:如果能从所有差评的词集,知道哪些词对分类结果其关键性作用,那么就可以给那些词赋予比较大的权重,然后让待分类句子的词集去乘上这个权重再做处理。
这种处理的关键还在于:设所有词相互独立,即词与词间没有关系。
步骤:
1.设差评分类为B1,现取所有差评的数据集DataSet1,所有词出现次数初始化为1,求出所有差评的词集p1Num,并且求出一共有多少词P1Denom(初始化为2)。
for i in range(DataSet_Count): if Label[i] == 1: p1Num += DataSet_Vec [i] p1Denom += sum(DataSet_Vec [i]) else: p0Num += DataSet_Vec [i] p0Denom += sum(DataSet_Vec [i])
更直观地,设以下两项均是标记为 1 的句子:
[1,0,0,1,0,1,1,0]
[0,0,0,1,0,1,1,0]
p1Num = [1,0,0,2,0,2,2,0]
p1Denom = 4 + 3 = 7
2.求:差评中,一个句子中某个词的出现概率
还是点1的计算实例:
P=[1,0,0,2,0,2,2,0] / 7 = [0.14, 0, 0, 0.29, 0, 0.29, 0.29, 0]
3. 处理待分类句子,求出其词集后分别乘上(矩阵乘法)好评词集权重、差评词集权重
设待分类句为testSentence:['love', 'my', 'dalmation']
句子词集是testVec: [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
([1,32]矩阵与[32,1]矩阵相乘,结果是一个数)
4.将利用步骤3得到的数,就是P(A|B),与差评率(差评总数/评论总数)相乘,得到待分类句子是差评率的结果。
P(AB) = P(A|B)P(B)
数据处理TIPS:
由于计算过程中可能存在许多很小的小数,可能会出现数据下溢问题(python相乘很小的数,四舍五入后得到0),所以可以采取对乘积取自然对数。例如,ln(a*b) = ln(a) + ln(b)。
所以求步骤3,可以这样处理:log(P * testVec^T),步骤4:result = log(P * testVec^T) + log(P(B))。注:此处的*是矩阵乘法。
朴素在哪?
设所有词相互独立,即词与词间没有关系。
局限:
1.分词,对于英文来说,通过空格、符号分词,可能可行,但中文来说应该挺麻烦,可能需要其他方法;
2.“朴素”让算法简单化,但其实词与词之间应该是有关系的,例如sit,sit后可能接on,可能没有,但不会是动词;对于句子的处理总有很多问题,分词,词的排序,词间关系,词的意思,等等有很多花样。
3.步骤3呈线程处理,可能还有些拓展空间;
4.关于空间使用上,就是三五万个词汇,好像也还好,毕竟像是神经网络模型都是动辄几万、几百万参数。