欢迎关注我的专栏( つ•̀ω•́)つ【人工智能通识】
【汇总】2019年4月专题
熵的定义
熵的概念起源于热力学Thermodynamic,而后又被克劳德·香农引入到信息学Information theory里面,后来熵的概念又由信息学扩展到计算机学、密码学、生物学、社会学等领域。
熵是一个人为定义的虚构概念,它表示了系统的无序性,可以计算得到但无法直接测量。
热力学熵
牛顿的经典力学世界,是以宏观的物体整体为研究对象的,从苹果到车辆到宇宙星球,这些并不涉及分子原子的微观领域。
17世纪末,活塞式蒸汽机问世,逐渐应用到采矿、纺织、冶金等产业。1776年,瓦特发明蒸汽机,大幅度提高蒸汽机的工作效率,开启第一次工业革命。在18世纪,热力学成为物理学科最重要的主旋律之一。
蒸汽机由高温气体驱动,而对于气体和能量的研究,科学家们明显感觉到经典牛顿力学的不足,19世纪70年代,奥地利物理学家玻尔兹曼Ludwig Edward Boltzmann提出了统计力学Statistical mechanics的概念,用微观分子领域的统计学特征来解释系统内热力学行为。
统计力学将气体宏观整体的温度、压力等属性表示为微观分子世界中分子行为的描述。当时认为,微观领域中这些分子仍然遵照牛顿力学特征,处于不停地运动状态,大量分子运动效果的统计数据形成了气体的宏观特征。
微观态和宏观态
微观态是指微观世界中所有粒子可能存在的某种状态。比如假定体积不变的情况下,有2个气体分子,其中一个能量是0,另一个能量是10,这一个微观态,对应宏观的能量属性就是10;但是也有另外一种可能,两个分子的能量分别是2和8,这又是一个不同的微观态,但对应的宏观态也是10;当然还有4好6,5和5等等,这些微观态都对应了同一个宏观态。
多个微观态可以对应同一个宏观态;但不能多个宏观态对应同一个微观态。可以把宏观态的特征看做微观粒子属性综合叠加、平均或者其他算法产生的统计结果。
两个分子的情况当然没有什么意义,因为1立方厘米空气中的分子个数就超过两千亿亿个。但是如果我们把装有众多气体分子的整个盒子视为一个系统,那么某个特定宏观态将可以对应巨量的微观态。
微观态是否是无限的?量子理论指出所有粒子所可能吸收或放射的能量数值并非是无限连续的,而是一份一份的,不能无限切割下去,也有特定的上限,不能释携带无限大的能量。
粗糙说就是分子的能量可以是0、1、2、3,但不能是1.2后者1.21341这样的无限细分,也不能大于3。这就约定了单个粒子的可能微观态是有限的,可以计算的。
每个粒子的可能微观态是有限的,那么一万个粒子共同组成的可能微观态也是有限可数的,而其中能够满足特定某个宏观态的对应的微观态数量更是可以计算的。
宏观态对应的所有可能的微观态的集合,就组成了它的相空间。
熵就是表示特定宏观态所对应的可能微观态的数量的多少。
那么为什么存在温度差的盒子的熵更小?(参照人工智能通识-科普-麦克斯韦妖)
假设一个盒子中只包含AB两个分子,每个分子能量的状态可以是0、1、2、3四种可能,那么整体宏观态属性(能量和)为4对应的可能微观态有1&3、2&2、3&1共3个,可以说熵是3;而如果我们要求AB一定要有温度差,左边低能右边高能,那么就只剩下1&3这一种微观态符合要求,熵是0,被确定了,就低于无限制的随机状态。
所以系统存在温差的时候熵较小,而在完全随机分布的热平衡状态熵较大。
从这里也可以知道,系统附有额外限定条件(比如要有温差)的宏观态对应的熵更小。
信息学熵
信息熵的概念是1948年克劳德·香农Claude Shannon提出来的。它表示随机生成器产生某种信息的频率,也就是表示无序性,和熵对应的是信息量(有序程度)。
比如有一个生成随机数的机器,它扔两次硬币,那么两次硬币正反面分布情况有四种。
如果有人告诉你说有一次它扔出了两个正面向上的(即11)情况,那么我们知道这个概率只有1/4,那么这句话的信息量就比较高,偶然性比较高;
如果说它扔出了一正一反(10或01),那么我们知道有一半的概率符合这个情况,那么这句话的信息量就比较低,偶然性不高;
如果说两个硬币都落地了,那么这句话就没什么信息量,基本等于废话,没有偶然性。
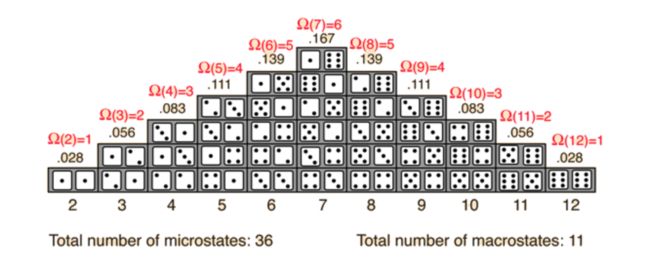
扔两次骰子,假设我们把投出的总数和视为宏观态,那么共11个宏观态对应了36个微观态,分布如下图:
我们看到其中投出总点数为7的有6种可能,六种随机可能,那么这里的熵比较高,如果已知总点数是7,再告诉你投出的是2和5,那么它出现的概率是1/6,这句话的信息量就比较高。
相反的,如果已知总点数是2,只有一种可能,没有随机性,所以它的熵是0,这时候再告诉你投出的是1和1,那么这句话没有任何信息量。
信息熵表示无序程度,可能有多么的随机,越多可能熵越高;信息量表示可以消除系统不确定性的能力,消除的越多信息量越高。
比如每天写日记,记录每天做的不同事情,由于你的生活每天的随机性都很大,重复性确定性都不高,那么就说你作为一个系统来说信息熵比较高,你每天写的内容信息量也比较大。但是如果你的日记就是每天写一下日期,然后记录毫无变化的起床、吃饭、上班、下班、睡觉,那么你这人作为一个系统来说信息熵就比较低,确定性很强,你写的这些东西也没什么信息量。
对于单个正常硬币而言,每次落地后正面向上或向下两种随机可能,所以有1比特的熵,每次落地产生的信息量也是1。
对于一个双面都是正面的硬币而言,这个系统的信息熵是0,没有不确定性,每次落地产生的信息量是0,不落地我们也知道它正面朝上,所以这个信息没价值。
在量子世界中,很多情况都是随机的,就是说量子世界的信息熵比较高,无序性随机性很强,我们得到的每个微观态的信息量也比较大;而在牛顿经典物理学中,一个物体开始运动时候一切就被确定下来了,接下来只是沿着既定的轨道运动,这时候我们去记录它所处的每个位置就没什么意义,包含的信息量也近乎为零。
所以,只有在信息熵非常大的系统中才能得到信息量大的内容,比如说彩票中奖号码。
一个宏观态(宏观系统)对应的微观态越多(相空间越大),那么它包含的信息熵越大,每个微观态所包含的信息量也就越大。
稍有些乱,后续会进一步梳理。
欢迎关注我的专栏( つ•̀ω•́)つ【人工智能通识】
每个人的智能新时代
如果您发现文章错误,请不吝留言指正;
如果您觉得有用,请点喜欢;
如果您觉得很有用,欢迎转载~
END