真实皮肤渲染简述
1、PBR
PBR(Physically Based Rendering) 基于物理的渲染,目的就是为了渲染效果更像真实世界中物体呈现的样子。一个例子就是金属质地物体的渲染。
PBR 的关键,在于两点:微表面模型和能量守恒。微表面模型假设模型表面是粗糙的,粗糙程度影响了光照在该表面反射的强弱。在实际的计算中我们假设一个粗糙度参数,该参数代表微表面法向量分布的方差或标准差。能量守恒的意义在于限制反射光线和折射光线的强度,使其和保持不变,否则违背真实物理定律。这两点会在后面的计算中体现出来。
反射率方程
下面是一个物理反射率方程(The Reflectance Equation)
\begin{align} L_o(p,\omega_o) = \int\limits_{\Omega} f_r(p,\omega_i,\omega_o) L_i(p,\omega_i) n \cdot \omega_i d\omega_i
\end{align}
我们知道在渲染方程中L代表通过某个无限小的立体角ωi在某个点上的辐射率,而立体角可以视作是入射方向向量ωi。注意我们利用光线和平面间的入射角的余弦值cosθ来计算能量,亦即从辐射率公式L转化至反射率公式时的n⋅ωi。用ωo表示观察方向,也就是出射方向,反射率公式计算了点p在ωo方向上被反射出来的辐射率Lo(p,ωo)的总和。或者换句话说:Lo表示了从ωo方向上观察,光线投射到点p上反射出来的辐照度。
上面这段来自 learnopengl 中文网站,看不懂也正常。需要理解的就是 Li 代表的是在单位面积(或者说单位点 p)上面的辐射率(可以简单理解爲所有光线的总能量或者说总强度),这里是不区分方向的,所以要算上 n 和 \(\omega_i\) 的点乘来计算真正反射的能量。
那么在光照计算时,研究者基于真实的反射率方程,提出了工程实用的渲染方程(Render Equation). 具体渲染方程长什么样子后面才能讲到,现在我们先来分析反射率方程中剩下的一项,Fr().
BRDF
双向反射分布函数(Bidirectional Reflective Distribution Function), 与表面材质有关,作为辐射率的系数或者说权重。接收的参数为光照方向,观察方向(出射方向),表面法线以及微表面粗糙度。
Cook-Torrance BRDF:
\begin{align}\ f_r = k_d f_{lambert} + k_s f_{cook-torrance} \end{align}
Kd 是折射光的比例,Ks 是反射光的比例。lambert 是一种漫反射的模拟,cook-torrance 是高光反射的模拟,公式如下:
\begin{align} f_{cook-torrance} = \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}
\end{align}
DFG 分别代表三种函数
- D: 正态分布函数,根据微表面假设,表面法线分布是一种正态分布,表示微表面法线与平均法线的偏离的概率
- F: Fresnel 菲涅尔方程,就是计算反射光和折射光的比例
- G: 物理函数,在皮肤渲染中可以忽略,详情看参考资料
Distribution
这个函数接收参数 n, 中间向量 h 和粗糙度 a.
\begin{align} NDF_{GGX TR}(n, h, \alpha) = \frac{\alpha^2}{\pi((n \cdot h)^2 (\alpha^2 - 1) + 1)^2}
\end{align}
用代码表示是:
float DistributionGGX(vec3 N, vec3 H, float roughness)
{
float a = roughness*roughness;
float a2 = a*a;
float NdotH = max(dot(N, H), 0.0);
float NdotH2 = NdotH*NdotH;
float nom = a2;
float denom = (NdotH2 * (a2 - 1.0) + 1.0);
denom = PI * denom * denom;
return nom / denom;
}Fresnel
Fresnel-Schlick近似法求得近似解:
\begin{align} F_{Schlick}(n, v, F_0) = F_0 + (1 - F_0) ( 1 - (n \cdot v))^5
\end{align}
F0 代表这个平面的基础反射率,不同的材质不一样。
总结
总之,最终的反射率方程如下:
\begin{align} L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)})L_i(p,\omega_i) n \cdot \omega_i d\omega_i
\end{align}
又,此处的 Fresnel 项 F 已经代表了平面的反射率,所以不再需要 \(k_s\) 了,直接去掉。
\[ L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)}) L_i(p,\omega_i) n \cdot \omega_i d\omega_i \]
2、皮肤渲染光照计算(BRDF)
首先,皮肤渲染还是属于 PBR 的一种,所以总体的渲染思路还是一致,仍然是按照 BRDF 来计算。
Fresnel
在内部的几个函数中,首先考虑 Fresnel 项,在皮肤渲染中 F0 取 0.028, 而且在针对皮肤这样的粗糙材质时使用 H 向量,而不是上文函数中的 n dot v(也就是法线与观察向量的点乘)。
float fresnelReflectance( float3 H, float3 V, float F0 ) {
float base = 1.0 - dot( V, H );
float exponential = pow( base, 5.0 );
return exponential + F0 * ( 1.0 - exponential );
}Beckmann Distribution
这里是一个优化的策略,将 distribution 项预先计算出来并存储在一个纹理内。在实际渲染的时候直接根据函数的两个参数在纹理上采样得到该点所对应的 D 函数的值。函数的参数即 n dot h 和代表粗糙度的系数 m. 计算方式如下:
float PHBeckmann( float ndoth, float m )
{
float alpha = acos( ndoth );
float ta = tan( alpha );
float val = 1.0/(m*m*pow(ndoth,4.0))*exp(-(ta*ta)/(m*m));
return val;
}值得注意的是这个和上面的分布函数是有区别的,这里采用了另一种计算方式,这是 beckmann 分布。
3、散射 (Scattering)
Diffusion profile
散射是皮肤渲染当中最重要的概念,也是皮肤这个材质,与其他的物理材质区别最大的一点。皮肤是有很多层的,光线在某个点入射以后,一部分光线被反射,另一部分光线被折射进入皮肤内部,在皮肤内部(特别是内部的不同的层次之间),光会被吸收,会发生散射现象,最后呢,在入射点附近的一个 3D 点上终止(也就是能量耗尽)或者射出表面。如果需要渲染逼真的皮肤表面,必须对此现象进行仿真。研究者假设光线进入皮肤后迅速向四周散射,在很少的几次散射后,光线就已经变成向各个方向平行地蔓延了。这样简化以后就提出了一个叫做 diffuse models 的模型。
再此基础上再次简化,研究者提出 diffusion profile 这个概念。这代表的是在一个表面上有一个光的发射点,有光在这个点向四周扩散,那么与这个点有不同距离的任意点,有多少光线到达了这个点,或者说分配到了多少的光的能量? diffusion profile 描述的就是光线传播的关系,给定一个距离可以得出该点的光的强度。这个函数是和 RGB 颜色的光有关的,红色的光有最强的扩散能力,能比另两种颜色的光传播更远的距离。根据这个概念,我们考虑皮肤的次表面散射的计算,在入射点射入的光线,向四周传播,其衰减的规律符合 diffusion profile. 那么在皮肤表面任意一点的话,需要考虑每一个入射点的次表面散射对该点的影响,将所有的结果累加就是最终的散射效果。因为皮肤下的散射现象发生得非常的迅速,所以我们几乎可以不考虑入射光线的方向,那么散射的计算就只需要考虑距离这一个因素就可以了。
那么究竟这个 profile 是怎样的呢?研究者发现可以用若干个不同系数的高斯函数来拟合这个函数。如下图我们可以看到,四个高斯函数和的拟合效果已经很接近原始函数了。这四个高斯函数的计算是这样的:
R(r) = 0.070G(0.036, r) + 0.18G(0.14, r) + 0.21G(0.91, r) + 0.29G(7.0, r).
Texture-Space Diffusion
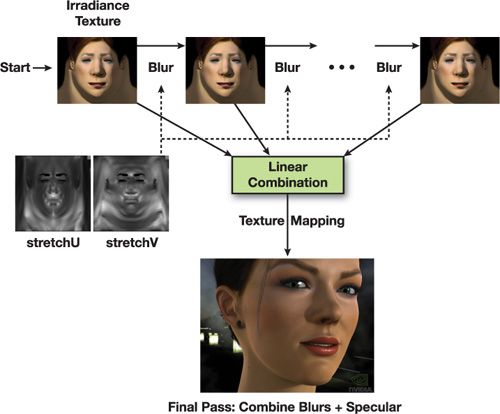
根据上述原理,真正实现皮肤表面次表面散射效果模拟的方法之一是在渲染前对纹理做若干次高斯卷积并累加,得到最终的纹理,用于渲染。
- 首先得到纹理
- 做 Skretch correction(可选)
- 将光照渲染出来(irradiance map),存入 off-screen texture
- 对每一个我们拟合 diffusion profile 的每一个高斯 kernel:
- 单独在 U 通道做模糊
- 单独在 V 通道做模糊
- 渲染 3D mesh:
- 使用每一个高斯处理后的纹理并将结果叠加
- 增加高光部分
Screen-Space Diffusion
这里介绍另一种更高效的做法,在屏幕空间做高斯模糊。效率提高点在于,前面的方法,需要计算出 irradiance map, 导致需要额外的操作才能重新获得 GPU 提供一些的便利,如 backface culling, viewport clipping. 而且计算 irradiance map 原本就需要费一些资源。另外前一种方法需要做两次顶点的坐标变换:在生成 irradiance map 的时候一次,最终渲染的时候一次。总而言之,屏幕空间的处理会更加高效。其流程与纹理空间的大同小异,首先将模型渲染出来,并且顺带就把漫反射部分的光照计算好带上了。在得到渲染结束的屏幕上的图像后,对皮肤部分做若干次高斯处理,然后再累加起来,然后加上高光部分,最终渲染这张图片就是处理后的结果了。
参考资料
PBR
Chapter 14. Advanced Techniques for Realistic Real-Time Skin Rendering
JORGE JIMENEZ, VERONICA SUNDSTEDT and DIEGO GUTIERREZ: Screen-Space Perceptual Rendering of Human Skin
http://www.iryoku.com/