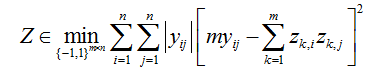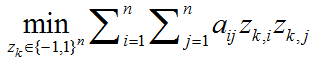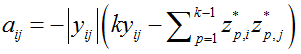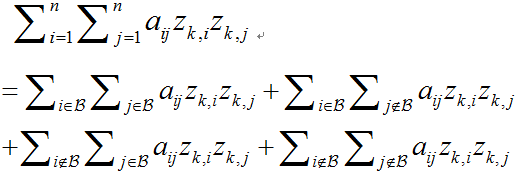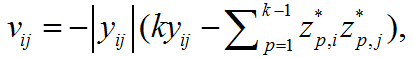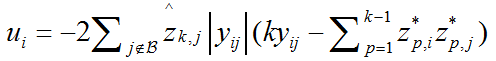Fast Supervised Hashing with Decision Trees for High-Dimensional Data

原文来源：http://blog.csdn.net/ying_xu/article/details/50570190

————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————

用决策树处理高维数据的一种快速监督性哈希

【摘要】监督性哈希旨在将原始特征映射成为能够保护汉明空间中基于标签的相似性的紧凑二进制编码。非线性哈希函数由于其强大的泛化能力而优于线性哈希函数。研究表明，核函数通常用来实现哈希中的非线性，并且以较缓慢的评估和训练时间作为代价可以实现良好的检索性能。本文分析了一种使用决策树来实现哈希的非线性方法，其评估和训练的速度快。首先提出对于哈希二进制编码推论问题的子模块公式化，和一种对于解决大规模推论的基于块搜索方法的高效图分割法。然后通过训练优化的决策树来学习哈希函数使得适用于二进制编码，并通过实验对以上算法进行了分析和结果的探讨。

【关键字】决策树监督性哈希 高维数据

1引言

哈希方法构造一系列的哈希函数，将原始的特征映射成为紧凑的二进制代码。哈希能够通过使用查找表或者基于排名的汉明空间实现快速的搜索。并且，紧凑的二进制代码对于大规模的数据存储非常有效。类似的应用有图像检索，大型对象检测等等。哈希方法旨在保留汉明空间中的一些概念的相似度或者称之为距离。这些方法可以被粗略地分为监督性方法和非监督性的方法。非监督性的方法努力保留原始特征空间的相似度。例如，局部敏感哈希（Locality-Sensitive Hashing, LSH）随机生成线性哈希函数来近似余弦相似度[1];谱哈希（SpectralHashing）学习保留高斯关联性的特征函数[2]；迭代量化（Iterative Quantization, ITQ）近似汉明空间中的欧氏距离[3]；在流形结构上的散列将内在流形结构考虑进去。

监督性的哈希被设计来保留一些基于标签的相似性。比如，这个可能发生在来自同一类型的图片被定义为彼此语义相似的情形。近年来，监督性哈希受到了越来越多的关注，比如有内核的监督哈希（KSH）[4]，两步哈希（TSH）[5]，二进制重建嵌入（BRE）[6]等。尽管监督性哈希对于现实应用更加灵活和吸引人，但是其学习速率比起非监督性哈希慢了许多。尽管现实情况是，哈希只有在被应用到大量的高维特征时才有着实用利益，大部分的监督性哈希方法仅仅被展示在相对小数目的低维特征上。比如，基于特征的码本在图像分类上获得了巨大的成功，其特征维数通常达到了数以万计[7]。为了利用这个特征学习的最新进展，对于监督性哈希能够在复杂的高维特征上有效处理大规模数据是非常需要的。为了填补这个差距，因此希望有一个监督性的哈希方法，能够利用大的训练集并有效利用高维特征。

非线性哈希函数，例如在KSH和TSH中使用到的核哈希函数，展示了比线性哈希函数很大的性能改进。然而，核函数对于在高维特征上的训练和测试的代价非常高。因此，一个有着非线性哈希函数的可扩展监督性哈希方法也是非常需要的。

2问题提出与分析

令χ = {x1,x2,...xn}⊆

表示一系列的训练点。基于标签的相似性信息保存在一个关联矩阵Y中，也就是监督性学习中的参考标准。Y中的元素

表示两个数据点

和

的相似度，且

 =

。特别地，如果两个点相似则

=1，如果两个点不相似则

= -1，如果两者之间的关系没有被定义，则

= 0。目标是学习一组哈希函数来保留汉明空间中基于标签的相似性。m个哈希函数表示成：

. 哈希函数的输出是m位的二进制代码:

。汉明关联性与汉明距离密切相关，是通过两个二进制编码的内积来计算的，计算公式为

。与KSH相似，基于汉明关联性来公式化哈希学习，使得相似数据对的关联性值为正，不相似数据对的关联性值为负。优化过程可以写为：

            

                                                  （1）

         其中，

用来避免未定义的数据对关系影响哈希的任务。因为如果关系没有定义的话，

=0，否则，

=1。因为使用决策树来作为哈希函数，因此定义每一个哈希函数为决策树的一个线性组合，即

                

                                                          （2）

其中，Q是决策树的数量。

表示有二进制输出的一个树函数。权重

和树

是用来学习一个哈希函数的参数。与核方法相比，决策树有着高维数据上更快的测试速度和非线性的适应能力。

直接学习决策树优化（1）显得比较困难，因此添加了辅助变量

作为

在处的第k个哈希函数的输出，即有

。显然，

是第i个数据点在第k位的二进制编码。有了这个辅助变量，（1）式就可以分解为两个子问题：

                   

                                      （3a）

                       

                                                  （3b）

其中Z是所有训练数据点的m位二进制的矩阵。式（3a）是一个二进制代码推理问题，式（3b）是一个简单的二分类问题。这样，原本复杂的监督性哈希的决策树学习就转化为两个相对简单的任务——解（3a）（步骤1）和（3b）（步骤2）。

步骤1：二进制代码推理

对于式（3a），顺序优化，一次优化一位，调节之前的位。当优化第k位时，（3a）的代价可以表示为：

             

  （4）

因此，对于第k位的优化可以等价公式化为一个二进制二次规划问题：

               

                                                           （5a）

其中，       

               

                                                              （5b）

这里

的表示前面位的二进制代码。使用一个阶段性的方案来解决每一位。特别地，当迭代到第k位时，位的长度设为k而不是m。这样，当前位的优化就取决于前面位产生的损失，通常这样的优化可以取得更好的推理结果。

由于该方法是需要处理高维的数据，因此采用一种对于二进制编码推论问题的子模块公式化，和一种有效地解决大规模的推理的基于块搜索的图分割方法。首先将数据点分成很多块，然后一次优化一个块的对应变量，同时调节剩下的变量。令 ℬ表示数据点的一个块。那么（5a）的代价可以表示为：

            

                 （6）

当优化一个块的时候，那些不存在目标块中的变量被设为常量。因此，对于一个块的优化也可以写成：

         

                    （7）

其中，表示不包含在目标块中的第k位的二进制编码。加上（5b）中对的定义，对于一个块的优化可以写成：

            

                               （8a）

其中，

           

                                        （8b）

             

                     （8c）

这里，

和

都是常量。构建一个块的关键是保证这样一个块的（8a）是子模块化的，因此这里可以应用有效的图分割法。实现算法（算法1）如下：

输入：关联矩阵：Y；位长度：k；最大推理迭代；块集：

；二进制码:

输出：一位的二进制码：

重复：

随机转置所有的块

对于每一个块

：

   使用图分割对每一个

进行（8a）的推论

   直到达到最大的迭代次数

特别地，在这个哈希问题中，通过利用相似度信息，可以很容易地构建满足子模块化要求的块，并引出如下命题。

命题1

如果

，（8a）中的优化是一个子模块化的问题。换句话说，对于块中的任意数据点，如果它不是与块中其他任意的数据点都不相似，那么（8a）就是子模块化的。

证明：如果

，

成立。那么，

。令

，那么有 

；

 。因此，

  ，

，因此证明了（8a）的子模块性。

只要满足命题1的条件，一个块可以使用许多种方式构建。一个简单的构造块的贪心算法（算法2）实现如下： 

输入：训练数据点：

 ，关联矩阵Y

输出：块：

重复：

t= t + 1；

；

：从V中随机选择；

初始化U为V和

的相似案例的并集；

对于U中的任何一个

：

   如果

与

中的任何点都不相似，那么

       将

加到

中；将

从V中移除

   直到V =∅

需要注意的是，块可以覆盖，它们的并集需要覆盖所有n个变量。，

步骤2：学习作为哈希函数的决策树

对于（3b）中的二分类问题，通常0-1损失被一些凸代理损失替代。这里，使用对于提升方法常用的指数型损耗。学习第k个哈希函数的分类问题可以写为：

              

                                （9）

这一步应用Adaboost来解决以上问题。在每一个提升的迭代中，一棵决策树和它的权重系数被学习。一棵二叉决策树的每一个节点是一个决策树桩。训练一个树桩是为了找到一个特征维和最小化权重分类误差的阈值。从这点上看，该方法是在同时进行特征选择和哈希函数的学习。可以简单利用已有可用的有效决策树学习技术来提高训练速度。最终使用一种高效的树桩实现算法[8]，比传统的方法大约快了10倍；特征量化能够在实践中无性能损失地大大提高训练速度，并且能大大减少内存消耗。线性量化特征值为256个容器；应用权重修剪技术，在每一个提升迭代中，最小的10%权重被修剪掉（被设置为0）；应用了LazyBoost技术：只有随机选取的特征维的一部分在树节点分裂中被评估使用。

因此，快速哈希方法的过程就可以表述为如下算法（算法3），实现过程如下：

输入：训练数据点：

；关联矩阵Y；位长度：m；块：

.

输出：哈希函数：

.

对于k = 1,…,m,

   第一步：调用算法1得到第k位的二进制码；

   第二步：训练（9）中的树得到哈希函数

；

   通过

的输出更新第k位的二进制码；

对于每一位，二进制码通过应用学习的哈希函数被更新。学习过的哈希函数能够对下一个的二进制码推论做出反馈，能够得到更好的性能。

3实验分析

实验所用编程语言为MATLAB，使用MATLAB的软件版本为MATLAB R2014b，数据集是采用MNIST进行训练和优化。MNIST是一个手写数字识别的数据集，包含60000个训练样本，10000个测试样本，是一个更大的数据集合NIST的一个子集。

在训练之前，需要生成数据的关联标签矩阵，即之前提到的Y。接着，为下面步骤的基于块的图分割生成推断块。至此，预处理结束。

接下来训练前参数的配置。实验所选用的二进制推断方法是基于块的Grapg-Cut方法，迭代次数为2。损失函数使用的是Hinge函数。针对步骤2中的分类器的设定，实验中使用的是boost_tree, boosting的迭代次数为200次，决策树的深度需要不断测试和修建，本实验室中决策树的深度设置为4，通常决策树的深度越深，得到的精度越好，但是训练速度会越慢。大的数据集需要要求更深的深度。对于权重的调整，一般取值为0.9~0.99之间，值越大，得到的精度越高，但是会减慢训练速度。该实验取值为0.99。lazyboost设置中，树节点分割的维度为200。

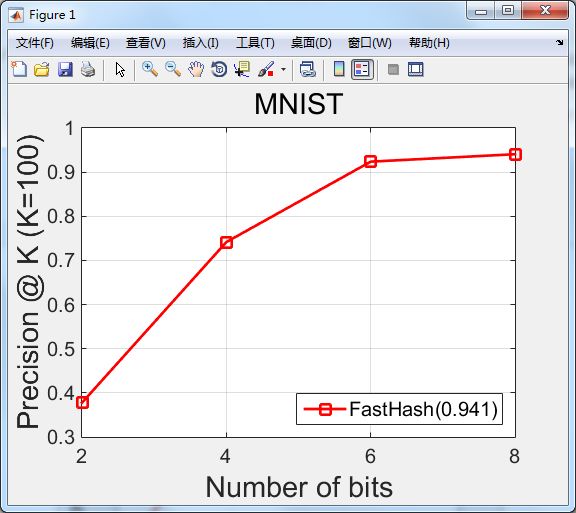
实验最后的检索精度有三种方式衡量：得到的检索样本前K个的正确率（也就是实验结果的纵坐标——精确度），平均准确率（MAP）和精确度-召回曲线下的面积。实验采用第一种尺度来衡量精确度，其中K取值100。横坐标是采用哈希决策树函数映射的二进制码位数，分别取2,4,6,8位，也可以取其他的值。

实验运行结果如下图1所示：

                                            

图1- 快速哈希的检索实验结果

   从实验的图形走势可以看出，随着位的数量增大，检索的精确度也随之提高，在bit位的数量达到8的时候，精确度已经达到94.1%。事实上，通过反复实验，最后也发现，实验的精确度在bit位数为8时稳定在0.937以上。

参考文献

[1]A. Gionis, P. Indyk,and R. Motwani. Similarity search in high dimensions via hashing. In Proc. Int. Conf. Very Large Data Bases (VLDB), 1999.1, 7

[2]Y. Weiss, R. Fergus,and A. Torralba.Multidimensional spectral hashing. In Proc. Eur. Conf. Comp. Vis. (ECCV), 2012. 1, 7

[3]Y. Gong, S. Lazebnik,A. Gordo, and F. Perronnin. Iterative quantization: a procrustean approach to learning binary codes for large-scaleimage retrieval. IEEE T. Pattern Analysis Mach. Intelli. (TPAMI), 2012. 1, 7

[4]W. Liu, J.Wang, R. Ji,Y. Jiang, and S. Chang. Supervised hashing with kernels. In Proc. IEEE Conf. Comp. Vis. Pattern Recogn. (CVPR), 2012. 1,2, 4, 6

[5]G. Lin, C. Shen, D.Suter, and A. van den Hengel. A general two-step approach to learning-based hashing. In Proc. Int. Conf. Comp. Vis.(ICCV), 2013. 1, 2, 4, 5

[6] B. Kulis and T.Darrell. Learning to hash with binary reconstructiveembeddings. In Proc. Adv. Neural Info. Process. Syst. (NIPS), 2009. 1, 4

[7] A. Coates and A. Ng. The importance of encoding versus training with sparsecoding and vectorquantization. In Proc. Int. Conf. Mach. Learn.(ICML), 2011.1, 4

[8] R. Appel, T. Fuchs, P.Doll´ar, and P. Perona. Quickly boosting decision trees-pruningunderachieving features early. In Proc. Int. Conf. Mach. Learn. (ICML), 2013. 3

顶1