软件工程实践2019第三次作业

软件工程实践2019第三次作业

---

1.Github项目地址

https://github.com/s031702143/031702143?files=1
（若超链接不行麻烦自己复制网址进去......）

2.PSP表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	30	50
Estimate	估计这个任务需要多少时间	60	120
Development	开发	240	380
Analysis	需求分析 (包括学习新技术)	60	500
Design Spec	生成设计文档	60	300
Design Review	设计复审	30	120
Coding Standard	代码规范 (为目前的开发制定合适的规范)	60	420
Design	具体设计	120	360
Coding	具体编码	60	360
Code Review	代码复审	120	180
Test	测试（自我测试，修改代码，提交修改）	120	180
Reporting	报告	30	60
Test Repor	测试报告	30	30
Size Measurement	计算工作量	30	20
Postmortem & Process Improvement Plan	事后总结, 并提出过程改进计划	15	50
合计		1065	3130

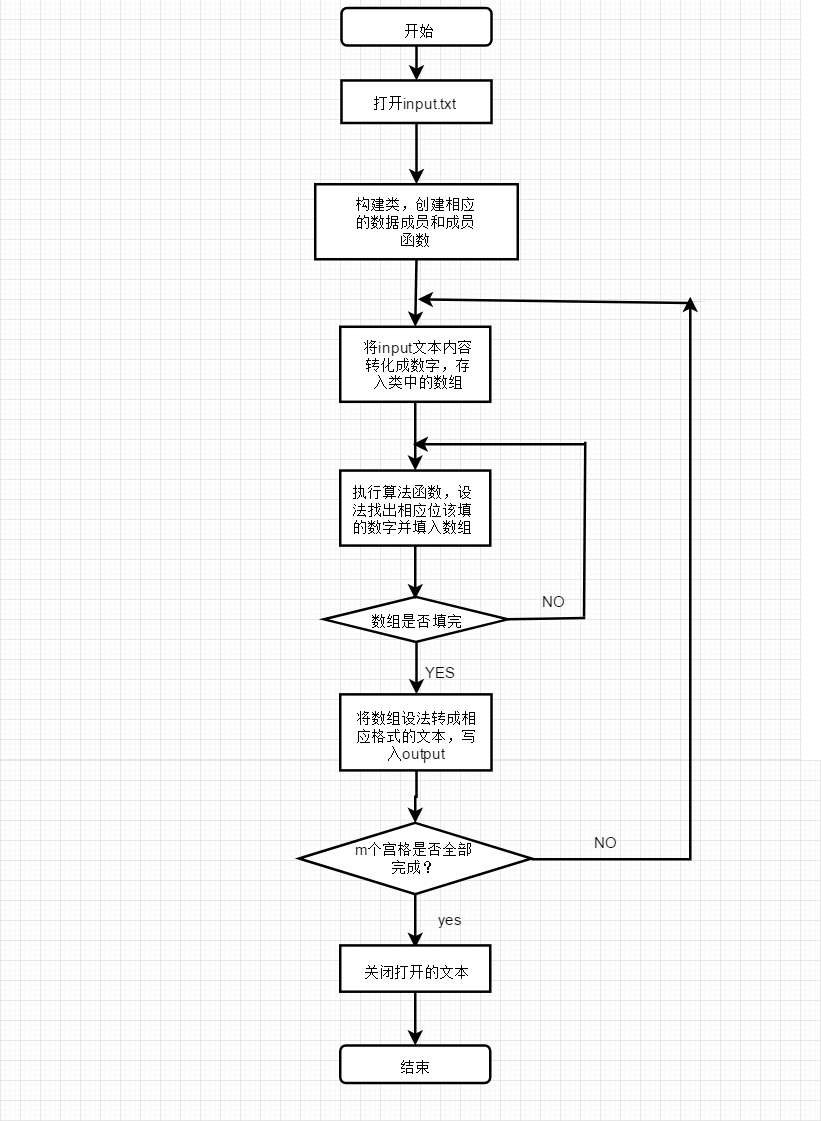
3.思路描述

按照平时玩数独的过程来进行求解，即根据游戏规则来完成。a[i][j]同一行同一列同一块若出现了x，则这一块不填x。直到所有宫格填完为止。

可以只根据这样的思路简单的构造函数、数组来求解，但还可以利用递归回溯的方法。

4.设计实现过程。设计包括代码如何组织，比如会有几个类，几个函数，他们之间关系如何，关键函数是否需要画出流程图？单元测试是怎么设计的？

代码设计中，先面向对象构造格子的类或九宫格的类。之后设计所需要的数据变量成员和成员函数。比如行检索，列检索和块检索，填入数字的函数，宫格类型的变量等等。
而我初始的想法就是对宫格二重循环，不停进行三种检索（当然，已经存了非零数字的方块不用检索），若某方块只剩下一种能填的可能，则填入这唯一的可能，若某个数字在同行同列同块的其他位置已经出现，则必然不可能填这种数字。

5.记录在改进程序性能上所花费的时间，描述你改进的思路。

在第一种想法时的改进有：在适当地时候进行continue循环或break循环，避免重复的执行不必要的步骤，还有对应每个方块用一个a[10]每个位置为0或1来决定能否存放下标i。
之后发现程序运行仍然不尽人意，于是进行思考、查阅资料，利用递归的算法来解决问题。这重新思考让我又花了很多的时间。

6.代码说明，并解释思路与注释说明。

几个主要的变量或函数。

        int arr[9][9] = { 0 };
    bool sign = false;
    int type;
    bool Check(int,int);
    int bianli(int);
    void _type(int x)
    {
        type = x;                   //写入宫格格式
    }
    void get_int(int, int, int);   //一次次读取，写入数组
    int out_int(int, int);
    void _false()
    {
        sign = false;            //每次完成宫格，要将其标志位还原为0,表示未填好
    }

将txt文本中的数据转换成字符数据存储在字符串in中。
之后每次循环从中提取出m*m个非'\0'、非'\n'字符，利用num=c-'0'将字符转换成数字存放进宫格。

string str = "\0";
string in = "\0";       //in用来存放input
    {
        // 接下来 从文件中读取数据
        fstream ifs;            //打开input 将内容存进in字符串
        ifs.open("input.txt", ios::in);
        if (!ifs) {
            cout << "open file fail!" << endl;
            return 1;
        }
        while (getline(ifs, str, '\0'))
        {
            in = in + str;
        }
        ifs.close();           //打开input文件后关闭
    };

递归的思想

//递归填入数字
int grid::bianli(int n)//用递归来解决数独
{
    if (sign)  return 1;
    if (n >= type * type)
    {
        sign = true;
        return 1;
    }
    if (arr[n / type][n % type] != 0)
    {
        bianli(n + 1);
    }
    else
    {
        for (int i = 1; i <= type; i++)   //i从1到9一次尝试
        {
            if (Check(n, i) == true)    //成功则填入i,进行下一次搜索
            {
                arr[n / type][n % type] = i;
                bianli(n + 1);
                if (sign == true) return 1;
                arr[n / type][n % type] = 0;     //不成功，把当前位还原为零，再次进行bianli(n)
            }
        }
    }
}

用来判断第n个格子中填入数字key是否合法，如99宫格中左上角的宫格为第0个，99宫格中右下角位第80个。
返回true代表填入合法，在继续执行递归。

bool Check(int n, int key)
{
    /*判断第n宫格所在行是否合法 */
    for (int i = 0; i < type; i++)
    {
        /* j为第n宫格的行 */
        int j = n / type;
        if (ge[j][i] == key) return false;
    }
    /* 判断第n宫格所在列是否合法 */
    for (int i = 0; i < type; i++)
    {
        /* j为第n宫格的列 */
        int j = n % type;
        if (ge[i][j] == key) return false;
    }

    /*x为第n宫格所在小m宫格左上角的行*/
    /*y为第n宫格所在小m宫格左上角的行*/
    int x = 0, y = 0;
    switch (type)   /* 判断n所在的小宫格是否合法，对于四宫格六宫格八宫格九宫格，模式一样但参数不同*/
    {
    case'4': {
        x = n / 4 / 2 * 2;
        y = n % 4 / 2 * 2;
        for (int i = x; i < x + 2; i++)
            for (int j = y; j < y + 2; j++)
                if (ge[i][j] == key) return false;
    }; break;
    case'6': {
        x = n / 6 / 2 * 2;
        y = n % 6 / 3 * 3;
        for (int i = x; i < x + 2; i++)
            for (int j = y; j < y + 3; j++)
                if (ge[i][j] == key) return false;
    }; break;
    case'8': {
        x = n / 8 / 4 * 4;
        y = n % 8 / 2 * 2;
        for (int i = x; i < x + 4; i++)
            for (int j = y; j < y + 2; j++)
                if (ge[i][j] == key) return false;
    }; break;
    case'9': {
        x = n / 9 / 3 * 3;
        y = n % 9 / 3 * 3;
        for (int i = x; i < x + 3; i++)
            for (int j = y; j < y + 3; j++)
                if (ge[i][j] == key) return false;
    }; break;
    default:
        break;
    }
    /* 全部合法，返回正确 */
    return true;
}

void grid::get_int(int x, int y, int num)
{
    arr[x][y] = num;          //将值输入给数组
}  
int grid::out_int(int i, int j)
{
    return arr[i][j];            //用来输出私有成员
}

有几个盘面则执行几次。

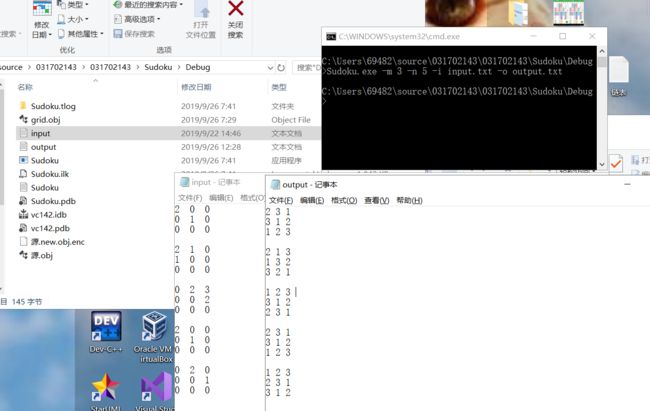
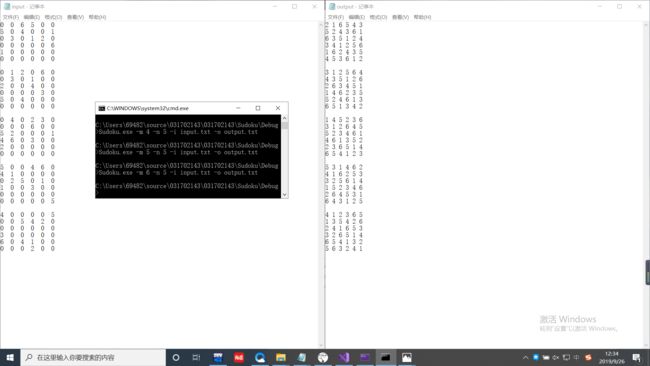
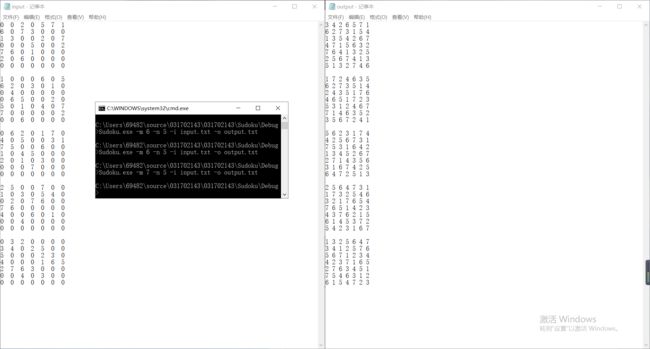
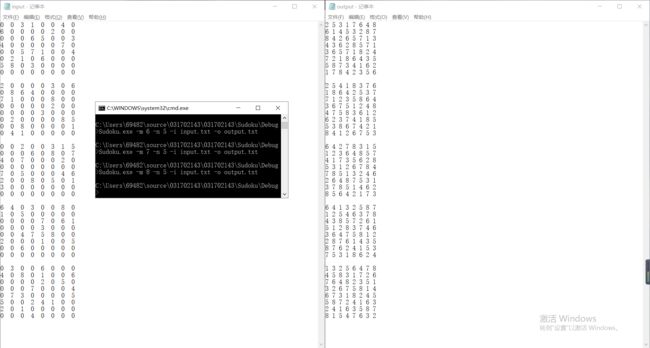
下面是执行结果：三至九阶

对于只有单独解的普通的数独（三至九阶），这个程序都能在较短时间内完成。但是对于多解的数独，程序只会输出一个解，这是因为一个解也是解，对于程序来说，只要完成某个方格，程序就会将n+1,进行下一个方格的求解，最后所有格都填完，回溯完成，程序结束。如下：

但这个数独的解有以下两种
1 2 4 5 3
4 1 3 2 5
5 4 1 3 2
2 3 5 1 4
3 5 2 4 1

1 2 4 5 3
4 1 3 2 5
5 4 1 3 2
2 3 5 4 1
3 5 2 1 4
并且此程序无法判断无解的情况。（改进方案以后尝试）

7.心路历程与收获

以前不是很经常打代码，而且知难而退，这次碰到题目对我来说挺难的，但是我一直在坚持打（实话）。好几天打到半夜三点（虽然还是打不出，切确的说是打出来，运行开在了程序执行递归那个地方），虽然自己水平不怎么样，最后的结果也还是不怎么样。有一个重要的改变与发现是：以前碰到不会的，我就有点敷衍了，这次我会努力去克服，我会去查我不会的东西，我会去问厉害的同学，我会去了解那些函数、参数各种东西。我知道了主函数还有参数，我知道了如何用c++打开txt、生成txt。以后我会去查我不会的东西并做好笔记，并且我知道接下来这段时间我应该要去学习输入输出流、更好地学习类与对象。