目录
- 一、什么是优先队列
- 二、什么是堆
- 三、堆的抽象数据类型描述
- 四、最大堆的操作
- 4.1 最大堆的创建
- 4.2 最大堆的插入
- 4.3 最大堆的删除
- 4.4 最大堆的建立
- 五、Python实现堆
- 5.1 上浮 shift up
- 5.2 下沉 shift_down
- 5.3 插入 push
- 5.4 弹出 pop
更新、更全的《数据结构与算法》的更新网站,更有python、go、人工智能教学等着你:https://www.cnblogs.com/nickchen121/p/11407287.html
一、什么是优先队列
优先队列(Priority Queue):特殊的队列,取出元素的顺序是依照元素的优先权(关键字)大小,而不是元素进入队列的先后顺序。
问题是:如何组织优先队列?我们可以通过以下三种方法:
- 一般的数组、链表
- 有序的数组或者链表
- 二叉搜索树?AVL树?
若采用数组或链表实现优先队列,我们可以看看它们在队列操作时的时间复杂度:
- 数组:
- 插入:元素总是插入尾部——\(\Theta(1)\)
- 删除:查找最大(或最小)关键字——\(\Theta(n)\)
- 从数组中删除时需要移动元素——\(O(n)\)
- 链表:
- 插入:元素总是插入链表的头部——\(\Theta(1)\)
- 删除:查找最大(或最小)关键字——\(\Theta(n)\)
- 删除结点——\(\Theta(1)\)
- 有序数组:
- 插入:找到合适的位置——\(O(n)或O(log_2n)\)
- 移动元素并插入——\(O(n)\)
- 删除:删除最后一个元素——\(\Theta(1)\)
- 插入:找到合适的位置——\(O(n)或O(log_2n)\)
- 有序链表:
- 插入:找到合适的位置——\(O(n)\)
- 插入元素——\(\Theta(1)\)
- 删除:删除首元素或最后元素——\(\Theta(1)\)
- 插入:找到合适的位置——\(O(n)\)
从上,我们可以看出,如果使用数组或链表的方式实现优先队列,在插入或者删除中,总会有一个操作方法的时间复杂度为O(n),因此我们是否可以考虑采用二叉树存储结构。
二、什么是堆
对于优先队列,如果采用二叉树存储结构,我们应该考虑一下两个问题:
- 是否可以采用二叉搜索树?
- 如果采用二叉树结构,应该更加关注插入还是删除
- 树结点顺序怎么安排?
- 树结构怎样?
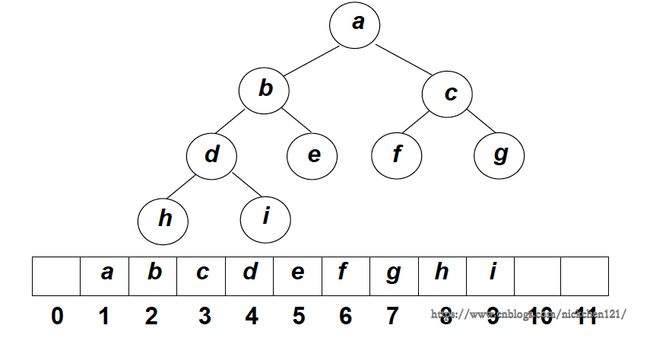
处于对上述问题的考虑,我们可以使用完全二叉树表示优先队列,如下图所示:
从上图我们可以看出堆的两个特性:
结构性:用数组表示的完全二叉树;
有序性:任一结点的关键字是其子树所有结点的最大值(或最小值)
- 最大堆(MaxHeap),也称大顶堆:最大值
- 最小堆(MinHeap),也称小顶堆:最小值
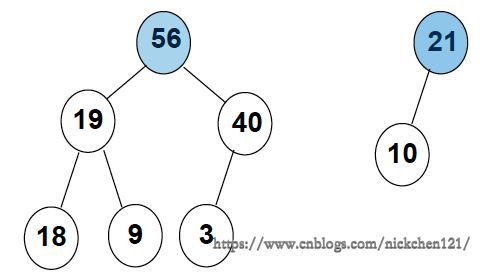
下图为最大堆图片:
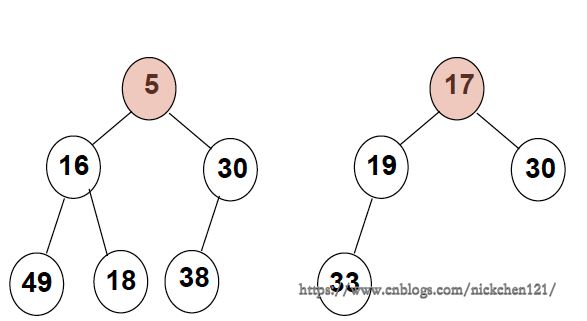
下图为最小堆图片:
从上述两幅图中,我们可以看出:从根节点到任意结点路径上结点序列的有序性!
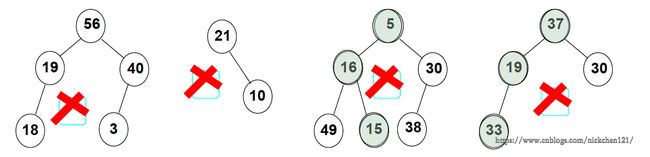
下图为不是堆的图片:
三、堆的抽象数据类型描述
类型名称:最大堆(MaxHeap)
数据对象集:完全二叉树,每个结点的元素值不小于其子结点的元素值
操作集:最大堆\(H\in{MaxHeap}\),元素\(item\in{ElementType}\),主要操作有:
MaxHeap Create(int MaxSize):创建一个空的最大堆;Boolean IsFull(MaxHeap H):判断最大堆H是否已满;Insert(MaxHeap H, ElementType item):将元素item插入最大堆H;Boolean IsEmpty(MaxHeap H):判断最大堆H是否为空;ElementType DeleteMax(MaxHeap H):返回H中最大元素(高优先级)。
四、最大堆的操作
4.1 最大堆的创建
/* c语言实现 */
typdef struct HeapStruct *MaxHeap;
struct HeapStruct{
ElementType *Elements; // 存储堆元素的数组
int Size; // 堆的当前元素个数
int Capacity; // 堆的最大容量
}
MaxHeap Create(int MaxSize)
{
// 创建容量为MaxSize的空的最大堆
MaxHeap H = malloc(sizeof(struct HeapStruct));
H->Elements = malloc((MaxSize + 1) * sizeof(ElementType));
H->Size = 0;
H->Capacity = MaxSize;
H->Elements[0] = MaxData; // 定义“哨兵”为大于堆中所有可能元素的值,便于以后更快操作 // 把MaxData换成小于堆中所有元素的MinData,同样适用于创建最小堆
return H;
}4.2 最大堆的插入
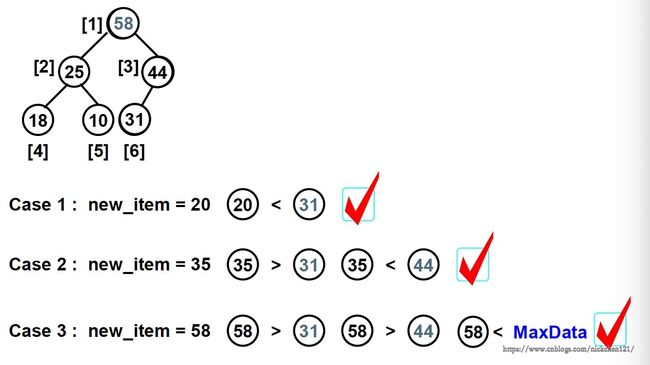
算法:将新增结点插入到从其父结点到根结点的有序序列中
/* c语言实现 */
void Insert(MaxHeap H, ElementType item)
{
// 将元素item插入最大堆H,其中H-Elements[0]已经定义为哨兵
int i;
if (IsFull(H)) {
printf("最大堆已满");
return ;
}
i = ++H->Size; // i指向插入后堆中的最后一个元素的位置
for (; H->Elements[i/2] < item; i /= 2)
H->Elements[i] = H->Elements[i/2]; // 向下过滤结点
H->Elements[i] = item; // 将item插入
}该插入操作的时间复杂度为:T(N) = O(log N)
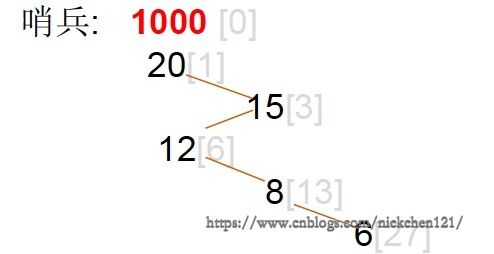
其中H->Element[0]是哨兵元素,它不小于堆中的最大元素,控制顺环结束,如下图所示:
4.3 最大堆的删除
取出根节点(最大值)元素,同时删除堆的一个结点。
/* c语言实现 */
ElementType DeleteMax(MaxHeap H)
{
// 从最大堆H中取出键值为最大的元素,并删除一个结点
int Parent, Child;
ElementType MaxItem, temp;
if (IsEmpty(H)){
printf("最大堆已为空");
return;
}
MaxItem = H->Elements[1]; // 取出根结点最大值
// 用最大堆中最后一个元素从根结点开始向上过滤下层结点
temp = H->Elements[H->Size--];
for (Parent = 1; Parent * 2 <= H->Size; Parent=Child) {
Child = Parent * 2;
if ((Child != H->Size) &&
(H->Elements[Child] < H->Elements[Child+1]))
Child ++; // Child指向左右子结点的较大者
if (temp >= H->Elements[Child]) break;
else // 移动temp元素到下一层
H->Elements[Parent] = H->Elements[Child];
}
H->Elements[Parent] = temp;
return MaxItem;
}该删除操作的时间复杂度为:T(N) = O(log N)
4.4 最大堆的建立
建立最大堆:将已经存在的N个元素按最大堆的要求存放在一个一维数组中
方法1:通过插入操作,将N个元素一个个相继插入到一个初始为空的堆中去,其时间代价最大为O(N logN)
方法2:通过下述2个步骤,在线性时间复杂度下建立最大堆
- 将N个元素按输入顺序存入,先满足完全二叉树的结构特性
- 调整各结点位置,以满足最大堆的有序特性
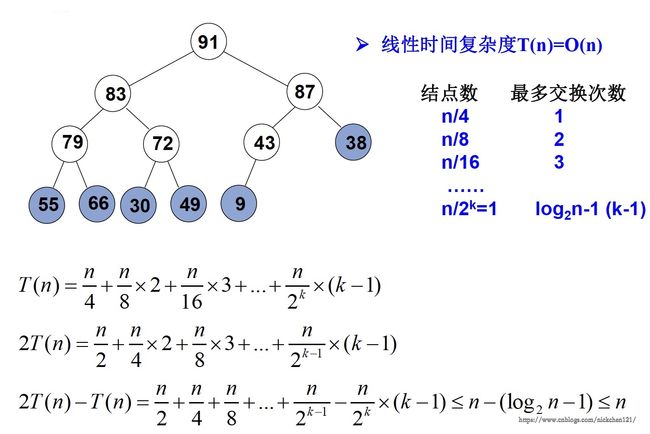
最大堆的建立如下图所示:
通过上图的演示,我们可以去测算最大堆建立时的线性复杂度为下图所示:
五、Python实现堆
5.1 上浮 shift up
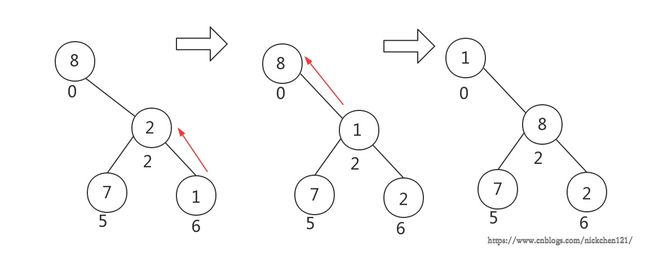
小根堆中越小的元素应该越在上面。以上图中6号位置元素1为例,它比它的父节点2小,则它应该和2交换位置,此时1在2号位置。这时1还比它的父节点8小,则它和8交换位置,1在0号位置了。此时1的位置是合理的。这个过程就叫上浮。总结一下就是:
从当前结点开始,和它的父亲节点比较,若是比父亲节点小,就交换,然后将当前询问的节点下标更新为原父亲节点下标;否则结束。
5.2 下沉 shift_down
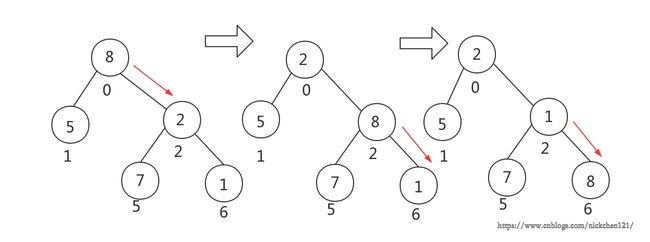
下沉的目的是让大元素沉在堆的下面。还以上图的子树为例,0位置的8的子节点5和2都比它小,最小的是2,则2和8交换位置,8沉到2号位置,此时它的子节点7和1也都比它小,最小的是1,那就和1交换位置,8沉到了6号位置,结束。
总结出下沉操作过程就是让当前结点的左右儿子(如果有的话)作比较,哪个比较小就和它交换,并更新询问节点的下标为被交换的儿子节点下标,否则结束。
5.3 插入 push
在向堆中插入元素时,我们总是将它放在堆的最后的位置,然后将它上浮,这样就能继续维持堆数据的有序性了。
5.4 弹出 pop
弹出操作演出的是堆顶的元素,也就是完全二叉树的根节点。若直接弹出根节点,则原来的一棵完全二叉树就变成两棵完全二叉树,这样对继续维护堆造成困难,此时我们将二叉树中最后位置的元素放到根节点位置,这样又是一棵完全二叉树了,然后将现在的根元素下沉就行。
以上是堆的一些操作的基本原理,但在python中实现堆时,操作过程略有不同。为了节省内存,在执行上浮操作时,不是逐次交换位置,而是拿着要上浮的元素去比较,找到合适的位置。下沉操作也是一样。
# python语言实现
class Heap:
def __init__(self, elist):
self._elems = list(elist)
if elist:
self.buildheap()
def is_empty(self):
return not self._elems
# 取堆顶元素
def peek(self):
if self.is_empty():
raise ValueError("堆为空")
return self._elems[0]
# 上浮
def siftup(self, e, last):
elems, i, j = self._elems, last, (last - 1) // 2
while i > 0 and e < elems[j]:
elems[i] = elems[j]
i, j = j, (j - 1) // 2
elems[i] = e
# 插入
def push(self, e):
self._elems.append(None)
self.siftup(e, len(self._elems) - 1)
# 下沉
def siftdown(self, e, begin, end):
elems, i, j = self._elems, begin, begin * 2 + 1
while j < end:
if j + 1 < end and elems[j + 1] < elems[j]:
j += 1
if e < elems[j]:
break
elems[i] = elems[j]
i = j
j = 2 * j + 1
elems[i] = e
# 弹出
def pop(self):
if self.is_empty():
raise ValueError("堆为空")
elems = self._elems
e0 = elems[0]
e = elems.pop()
if len(elems) > 0:
self.siftdown(e, 0, len(elems))
return e0
# 从数组构建堆
def buildheap(self):
end = len(self._elems)
for i in range(end // 2 - 1, -1, -1):
self.siftdown(self._elems[i], i, end)