本篇文章介绍EasyPR里新的定位功能:颜色定位与偏斜扭正。希望这篇文档可以帮助开发者与使用者更好的理解EasyPR的设计思想。
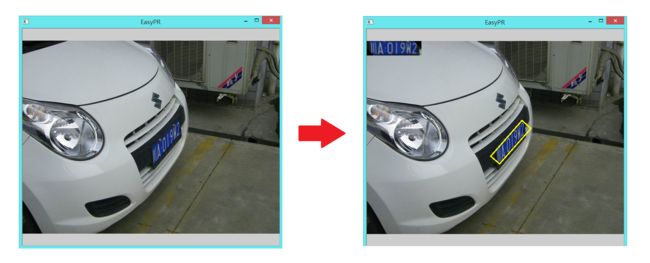
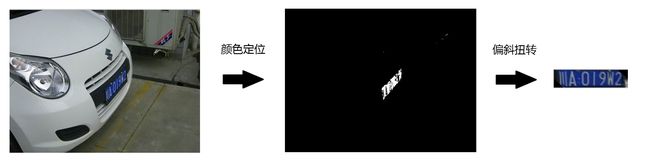
让我们先看一下示例图片,这幅图片中的车牌通过颜色的定位法进行定位并从偏斜的视角中扭正为正视角(请看右图的左上角)。
图1 新版本的定位效果
下面内容会对这两个特性的实现过程展开具体的介绍。首先介绍颜色定位的原理,然后是偏斜扭正的实现细节。
由于本文较长,为方便读者,以下是本文的目录:
一.颜色定位
1.1起源
1.2方法
1.3不足与改善
二.偏斜扭正
2.1分析
2.2ROI截取
2.3扩大化旋转
2.4偏斜判断
2.5仿射变换
2.6总结
三.总结
一. 颜色定位
1.起源
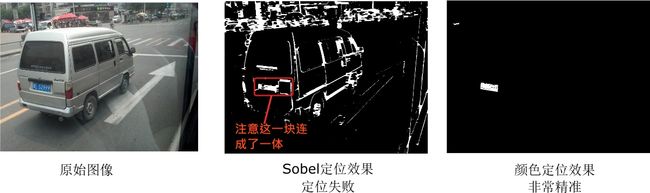
在前面的介绍里,我们使用了Sobel查找垂直边缘的方法,成功定位了许多车牌。但是,Sobel法最大的问题就在于面对垂直边缘交错的情况下,无法准确地定位车牌。例如下图。为了解决这个问题,可以考虑使用颜色信息进行定位。
图2 颜色定位与Sobel定位的比较
如果将颜色定位与Sobel定位加以结合的话,可以使车牌的定位准确率从75%上升到94%。
2.方法
关于颜色定位首先我们想到的解决方案就是:利用RGB值来判断。
这个想法听起来很自然:如果我们想找出一幅图像中的蓝色部分,那么我们只需要检查RGB分量(RGB分量由Red分量--红色,Green分量--绿色,Blue分量--蓝色共同组成)中的Blue分量就可以了。一般来说,Blue分量是个0到255的值。如果我们设定一个阈值,并且检查每个像素的Blue分量是否大于它,那我们不就可以得知这些像素是不是蓝色的了么?这个想法虽然很好,不过存在一个问题,我们该怎么来选择这个阈值?这是第一个问题。
即便我们用一些方法决定了阈值以后,那么下面的一个问题就会让人抓狂,颜色是组合的,即便蓝色属性在255(这样已经很‘蓝’了吧),只要另外两个分量配合(例如都为255),你最后得到的不是蓝色,而是黑色。
这还只是区分蓝色的问题,黄色更麻烦,它是由红色和绿色组合而成的,这意味着你需要考虑两个变量的配比问题。这些问题让选择RGB颜色作为判断的难度大到难以接受的地步。因此必须另想办法。
为了解决各种颜色相关的问题,人们发明了各种颜色模型。其中有一个模型,非常适合解决颜色判断的问题。这个模型就是HSV模型。
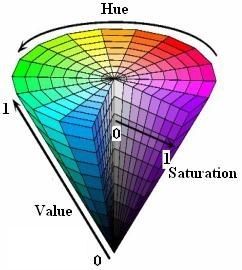
图3 HSV颜色模型
HSV模型是根据颜色的直观特性创建的一种圆锥模型。与RGB颜色模型中的每个分量都代表一种颜色不同的是,HSV模型中每个分量并不代表一种颜色,而分别是:色调(H),饱和度(S),亮度(V)。
H分量是代表颜色特性的分量,用角度度量,取值范围为0~360,从红色开始按逆时针方向计算,红色为0,绿色为120,蓝色为240。S分量代表颜色的饱和信息,取值范围为0.0~1.0,值越大,颜色越饱和。V分量代表明暗信息,取值范围为0.0~1.0,值越大,色彩越明亮。
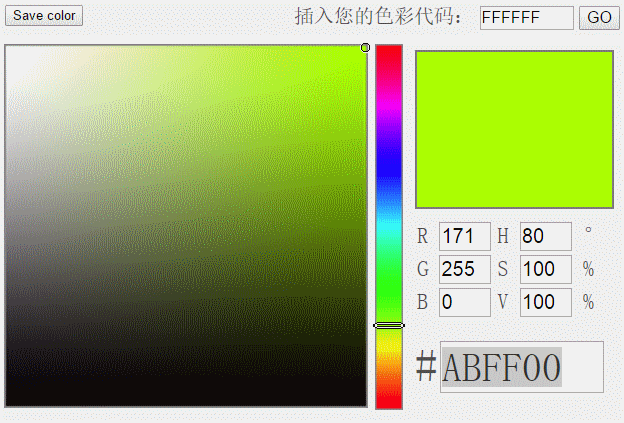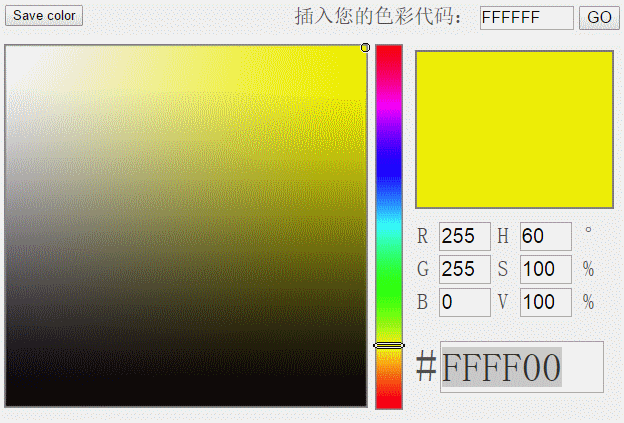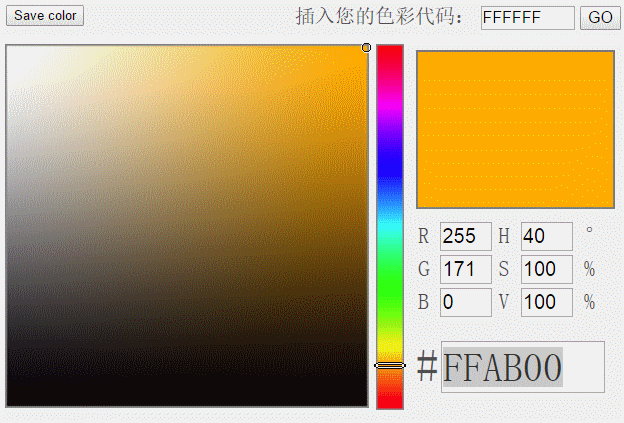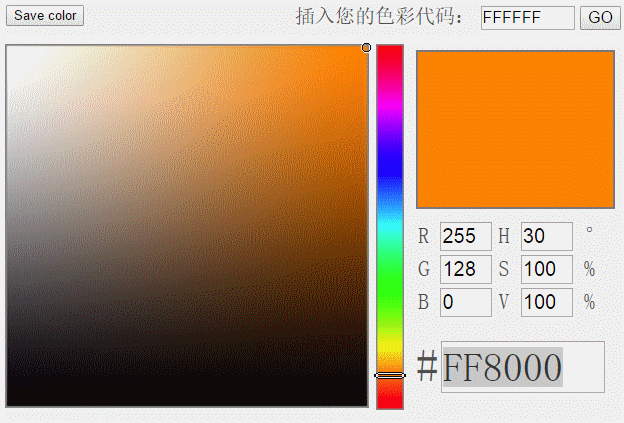
H分量是HSV模型中唯一跟颜色本质相关的分量。只要固定了H的值,并且保持S和V分量不太小,那么表现的颜色就会基本固定。为了判断蓝色车牌颜色的范围,可以固定了S和V两个值为1以后,调整H的值,然后看颜色的变化范围。通过一段摸索,可以发现当H的取值范围在200到280时,这些颜色都可以被认为是蓝色车牌的颜色范畴。于是我们可以用H分量是否在200与280之间来决定某个像素是否属于蓝色车牌。黄色车牌也是一样的道理,通过观察,可以发现当H值在30到80时,颜色的值可以作为黄色车牌的颜色。
这里的颜色表来自于这个网站。
下图显示了蓝色的H分量变化范围。
图4 蓝色的H分量区间
下图显示了黄色的H分量变化范围。
图5 黄色的H分量区间
光判断H分量的值是否就足够了?
事实上是不足的。固定了H的值以后,如果移动V和S会带来颜色的饱和度和亮度的变化。当V和S都达到最高值,也就是1时,颜色是最纯正的。降低S,颜色越发趋向于变白。降低V,颜色趋向于变黑,当V为0时,颜色变为黑色。因此,S和V的值也会影响最终颜色的效果。
我们可以设置一个阈值,假设S和V都大于阈值时,颜色才属于H所表达的颜色。
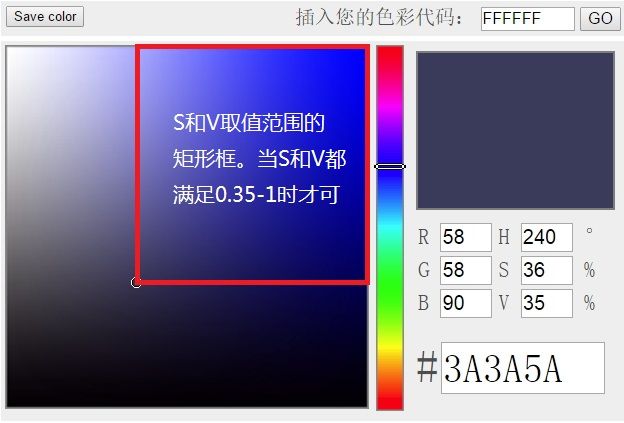
在EasyPR里,这个值是0.35,也就是V属于0.35到1且S属于0.35到1的一个范围,类似于一个矩形。对V和S的阈值判断是有必要的,因为很多车牌周身的车身,都是H分量属于200-280,而V分量或者S分量小于0.35的。通过S和V的判断可以排除车牌周围车身的干扰。
图6 V和S的区间
明确了使用HSV模型以及用阈值进行判断以后,下面就是一个颜色定位的完整过程。
第一步,将图像的颜色空间从RGB转为HSV,在这里由于光照的影响,对于图像使用直方图均衡进行预处理;
第二步,依次遍历图像的所有像素,当H值落在200-280之间并且S值与V值也落在0.35-1.0之间,标记为白色像素,否则为黑色像素;
第三步,对仅有白黑两个颜色的二值图参照原先车牌定位中的方法,使用闭操作,取轮廓等方法将车牌的外接矩形截取出来做进一步的处理。
图7 蓝色定位效果
以上就完成了一个蓝色车牌的定位过程。我们把对图像中蓝色车牌的寻找过程称为一次与蓝色模板的匹配过程。代码中的函数称之为colorMatch。一般说来,一幅图像需要进行一次蓝色模板的匹配,还要进行一次黄色模板的匹配,以此确保蓝色和黄色的车牌都被定位出来。
黄色车牌的定位方法与其类似,仅仅只是H阈值范围的不同。事实上,黄色定位的效果一般好的出奇,可以在非常复杂的环境下将车牌极为准确的定位出来,这可能源于现实世界中黄色非常醒目的原因。
图8 黄色定位效果
从实际效果来看,颜色定位的效果是很好的。在通用数据测试集里,大约70%的车牌都可以被定位出来(一些颜色定位不了的,我们可以用Sobel定位处理)。
在代码中有些细节需要注意:
一. opencv为了保证HSV三个分量都落在0-255之间(确保一个char能装的下),对H分量除以了2,也就是0-180的范围,S和V分量乘以了255,将0-1的范围扩展到0-255。我们在设置阈值的时候需要参照opencv的标准,因此对参数要进行一个转换。
二. 是v和s取值的问题。对于暗的图来说,取值过大容易漏,而对于亮的图,取值过小则容易跟车身混淆。因此可以考虑最适应的改变阈值。
三. 是模板问题。目前的做法是针对蓝色和黄色的匹配使用了两个模板,而不是统一的模板。统一模板的问题在于担心蓝色和黄色的干扰问题,例如黄色的车与蓝色的牌的干扰,或者蓝色的车和黄色牌的干扰,这里面最典型的例子就是一个带有蓝色车牌的黄色出租车,在很多城市里这已经是“标准配置”。因此需要将蓝色和黄色的匹配分别用不同的模板处理。
了解完这三个细节以后,下面就是代码部分。
//! 根据一幅图像与颜色模板获取对应的二值图 //! 输入RGB图像, 颜色模板(蓝色、黄色) //! 输出灰度图(只有0和255两个值,255代表匹配,0代表不匹配) Mat colorMatch(const Mat& src, Mat& match, const Color r, const bool adaptive_minsv) { // S和V的最小值由adaptive_minsv这个bool值判断 // 如果为true,则最小值取决于H值,按比例衰减 // 如果为false,则不再自适应,使用固定的最小值minabs_sv // 默认为false const float max_sv = 255; const float minref_sv = 64; const float minabs_sv = 95; //blue的H范围 const int min_blue = 100; //100 const int max_blue = 140; //140 //yellow的H范围 const int min_yellow = 15; //15 const int max_yellow = 40; //40 Mat src_hsv; // 转到HSV空间进行处理,颜色搜索主要使用的是H分量进行蓝色与黄色的匹配工作 cvtColor(src, src_hsv, CV_BGR2HSV); vectorhsvSplit; split(src_hsv, hsvSplit); equalizeHist(hsvSplit[2], hsvSplit[2]); merge(hsvSplit, src_hsv); //匹配模板基色,切换以查找想要的基色 int min_h = 0; int max_h = 0; switch (r) { case BLUE: min_h = min_blue; max_h = max_blue; break; case YELLOW: min_h = min_yellow; max_h = max_yellow; break; } float diff_h = float((max_h - min_h) / 2); int avg_h = min_h + diff_h; int channels = src_hsv.channels(); int nRows = src_hsv.rows; //图像数据列需要考虑通道数的影响; int nCols = src_hsv.cols * channels; if (src_hsv.isContinuous())//连续存储的数据,按一行处理 { nCols *= nRows; nRows = 1; } int i, j; uchar* p; float s_all = 0; float v_all = 0; float count = 0; for (i = 0; i < nRows; ++i) { p = src_hsv.ptr (i); for (j = 0; j < nCols; j += 3) { int H = int(p[j]); //0-180 int S = int(p[j + 1]); //0-255 int V = int(p[j + 2]); //0-255 s_all += S; v_all += V; count++; bool colorMatched = false; if (H > min_h && H < max_h) { int Hdiff = 0; if (H > avg_h) Hdiff = H - avg_h; else Hdiff = avg_h - H; float Hdiff_p = float(Hdiff) / diff_h; // S和V的最小值由adaptive_minsv这个bool值判断 // 如果为true,则最小值取决于H值,按比例衰减 // 如果为false,则不再自适应,使用固定的最小值minabs_sv float min_sv = 0; if (true == adaptive_minsv) min_sv = minref_sv - minref_sv / 2 * (1 - Hdiff_p); // inref_sv - minref_sv / 2 * (1 - Hdiff_p) else min_sv = minabs_sv; // add if ((S > min_sv && S < max_sv) && (V > min_sv && V < max_sv)) colorMatched = true; } if (colorMatched == true) { p[j] = 0; p[j + 1] = 0; p[j + 2] = 255; } else { p[j] = 0; p[j + 1] = 0; p[j + 2] = 0; } } } //cout << "avg_s:" << s_all / count << endl; //cout << "avg_v:" << v_all / count << endl; // 获取颜色匹配后的二值灰度图 Mat src_grey; vector hsvSplit_done; split(src_hsv, hsvSplit_done); src_grey = hsvSplit_done[2]; match = src_grey; return src_grey; }
3.不足
以上说明了颜色定位的设计思想与细节。那么颜色定位是不是就是万能的?答案是否定的。在色彩充足,光照足够的情况下,颜色定位的效果很好,但是在面对光线不足的情况,或者蓝色车身的情况时,颜色定位的效果很糟糕。下图是一辆蓝色车辆,可以看出,车牌与车身内容完全重叠,无法分割。
图9 失效的颜色定位
碰到失效的颜色定位情况时需要使用原先的Sobel定位法。
目前的新版本使用了颜色定位与Sobel定位结合的方式。首先进行颜色定位,然后根据条件使用Sobel进行再次定位,增加整个系统的适应能力。
为了加强鲁棒性,Sobel定位法可以用两阶段的查找。也就是在已经被Sobel定位的图块中,再进行一次Sobel定位。这样可以增加准确率,但会降低了速度。一个折衷的方案是让用户决定一个参数m_maxPlates的值,这个值决定了你在一幅图里最多定位多少车牌。系统首先用颜色定位出候选车牌,然后通过SVM模型来判断是否是车牌,最后统计数量。如果这个数量大于你设定的参数,则认为车牌已经定位足够了,不需要后一步处理,也就不会进行两阶段的Sobel查找。相反,如果这个数量不足,则继续进行Sobel定位。
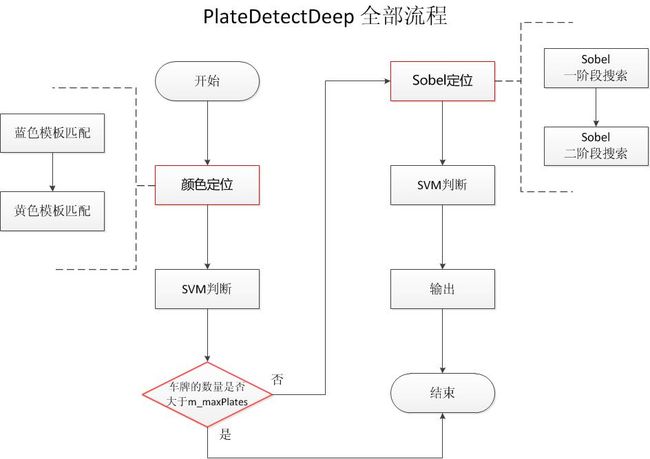
综合定位的代码位于CPlateDectec中的的成员函数plateDetectDeep中,以下是plateDetectDeep的整体流程。
图10 综合定位全部流程
有没有颜色定位与Sobel定位都失效的情况?有的。这种情况下可能需要使用第三类定位技术--字符定位技术。这是EasyPR发展的一个方向,这里不展开讨论。
二. 偏斜扭转
解决了颜色的定位问题以后,下面的问题是:在定位以后,我们如何把偏斜过来的车牌扭正呢?
图11 偏斜扭转效果
这个过程叫做偏斜扭转过程。其中一个关键函数就是opencv的仿射变换函数。但在具体实施时,有很多需要解决的问题。
1.分析
在任何新的功能开发之前,技术预研都是第一步。
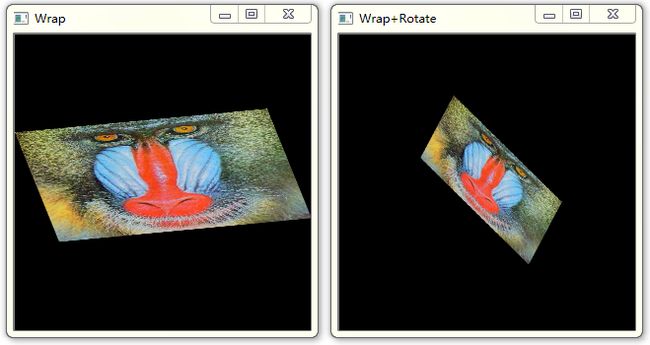
在这篇文档介绍了opencv的仿射变换功能。效果见下图。
图12 仿射变换效果
仔细看下,貌似这个功能跟我们的需求很相似。我们的偏斜扭转功能,说白了,就是把对图像的观察视角进行了一个转换。
不过这篇文章里的代码基本来自于另一篇官方文档。官方文档里还有一个例子,可以矩形扭转成平行四边形。而我们的需求正是将平行四边形的车牌扭正成矩形。这么说来,只要使用例子中对应的反函数,应该就可以实现我们的需求。从这个角度来看,偏斜扭转功可以实现。确定了可行性以后,下一步就是思考如何实现。
在原先的版本中,我们对定位出来的区域会进行一次角度判断,当角度小于某个阈值(默认30度)时就会进行全图旋转。
这种方式有两个问题:
一是我们的策略是对整幅图像旋转。对于opencv来说,每次旋转操作都是一个矩形的乘法过程,对于非常大的图像,这个过程是非常消耗计算资源的;
二是30度的阈值无法处理示例图片。事实上,示例图片的定位区域的角度是-50度左右,已经大于我们的阈值了。为了处理这样的图片,我们需要把我们的阈值增大,例如增加到60度,那么这样的结果是带来候选区域的增多。
两个因素结合,会大幅度增加处理时间。为了不让处理速度下降,必须想办法规避这些影响。
一个方法是不再使用全图旋转,而是区域旋转。其实我们在获取定位区域后,我们并不需要定位区域以外的图像。
倘若我们能划出一块小的区域包围定位区域,然后我们仅对定位区域进行旋转,那么计算量就会大幅度降低。而这点,在opencv里是可以实现的,我们对定位区域RotatedRect用boundingRect()方法获取外接矩形,再使用Mat(Rect ...)方法截取这个区域图块,从而生成一个小的区域图像。于是下面的所有旋转等操作都可以基于这个区域图像进行。
在这些设计决定以后,下面就来思考整个功能的架构。
我们要解决的问题包括三类,第一类是正的车牌,第二类是倾斜的车牌,第三类是偏斜的车牌。前两类是前面说过的,第三类是本次新增的功能需求。第二类倾斜车牌与第三类车牌的区别见下图。
图13 两类不同的旋转
通过上图可以看出,正视角的旋转图片的观察角度仍然是正方向的,只是由于路的不平或者摄像机的倾斜等原因,导致矩形有一定倾斜。这类图块的特点就是在RotataedRect内部,车牌部分仍然是个矩形。偏斜视角的图片的观察角度是非正方向的,是从侧面去看车牌。这类图块的特点是在RotataedRect内部,车牌部分不再是个矩形,而是一个平行四边形。这个特性决定了我们需要区别的对待这两类图片。
一个初步的处理思路就是下图。
图14 分析实现流程
简单来说,整个处理流程包括下面四步:
1.感兴趣区域的截取
2.角度判断
3.偏斜判断
4.仿射变换
接下来按照这四个步骤依次介绍。
2.ROI截取
如果要使用区域旋转,首先我们必须从原图中截取出一个包含定位区域的图块。
opencv提供了一个从图像中截取感兴趣区域ROI的方法,也就是Mat(Rect ...)。这个方法会在Rect所在的位置,截取原图中一个图块,然后将其赋值到一个新的Mat图像里。遗憾的是这个方法不支持RotataedRect,同时Rect与RotataedRect也没有继承关系。因此布不能直接调用这个方法。
我们可以使用RotataedRect的boudingRect()方法。这个方法会返回一个RotataedRect的最小外接矩形,而且这个矩形是一个Rect。因此将这个Rect传递给Mat(Rect...)方法就可以截取出原图的ROI图块,并获得对应的ROI图像。
需要注意的是,ROI图块和ROI图像的区别,当我们给定原图以及一个Rect时,原图中被Rect包围的区域称为ROI图块,此时图块里的坐标仍然是原图的坐标。当这个图块里的内容被拷贝到一个新的Mat里时,我们称这个新Mat为ROI图像。ROI图像里仅仅只包含原来图块里的内容,跟原图没有任何关系。所以图块和图像虽然显示的内容一样,但坐标系已经发生了改变。在从ROI图块到ROI图像以后,点的坐标要计算一个偏移量。
下一步的工作中可以仅对这个ROI图像进行处理,包括对其旋转或者变换等操作。
示例图片中的截取出来的ROI图像如下图:
图15 截取后的ROI图像
在截取中可能会发生一个问题。如果直接使用boundingRect()函数的话,在运行过程中会经常发生这样的异常。OpenCV Error: Assertion failed (0 <= roi.x && 0 <= roi.width && roi.x + roi.width <= m.cols && 0 <= roi.y && 0 <= roi.height && roi.y + roi.height <= m.rows) incv::Mat::Mat,如下图。
图16 不安全的外接矩形函数会抛出异常
这个异常产生的原因在于,在opencv2.4.8中(不清楚opencv其他版本是否没有这个问题),boundingRect()函数计算出的Rect的四个点的坐标没有做验证。这意味着你计算一个RotataedRect的最小外接矩形Rect时,它可能会给你一个负坐标,或者是一个超过原图片外界的坐标。于是当你把Rect作为参数传递给Mat(Rect ...)的话,它会提示你所要截取的Rect中的坐标越界了!
解决方案是实现一个安全的计算最小外接矩形Rect的函数,在boundingRect()结果之上,对角点坐标进行一次判断,如果值为负数,就置为0,如果值超过了原始Mat的rows或cols,就置为原始Mat的这些rows或cols。
这个安全函数名为calcSafeRect(...),下面是这个函数的代码。
//! 计算一个安全的Rect //! 如果不存在,返回false bool CPlateLocate::calcSafeRect(const RotatedRect& roi_rect, const Mat& src, Rect_<float>& safeBoundRect) { Rect_<float> boudRect = roi_rect.boundingRect(); // boudRect的左上的x和y有可能小于0 float tl_x = boudRect.x > 0 ? boudRect.x : 0; float tl_y = boudRect.y > 0 ? boudRect.y : 0; // boudRect的右下的x和y有可能大于src的范围 float br_x = boudRect.x + boudRect.width < src.cols ? boudRect.x + boudRect.width - 1 : src.cols - 1; float br_y = boudRect.y + boudRect.height < src.rows ? boudRect.y + boudRect.height - 1 : src.rows - 1; float roi_width = br_x - tl_x; float roi_height = br_y - tl_y; if (roi_width <= 0 || roi_height <= 0) return false; // 新建一个mat,确保地址不越界,以防mat定位roi时抛异常 safeBoundRect = Rect_<float>(tl_x, tl_y, roi_width, roi_height); return true; }
3.扩大化旋转
好,当我通过calcSafeRect(...)获取了一个安全的Rect,然后通过Mat(Rect ...)函数截取了这个感兴趣图像ROI以后。下面的工作就是对这个新的ROI图像进行操作。
首先是判断这个ROI图像是否要旋转。为了降低工作量,我们不对角度在-5度到5度区间的ROI进行旋转(注意这里讲的角度针对的生成ROI的RotataedRect,ROI本身是水平的)。因为这么小的角度对于SVM判断以及字符识别来说,都是没有影响的。
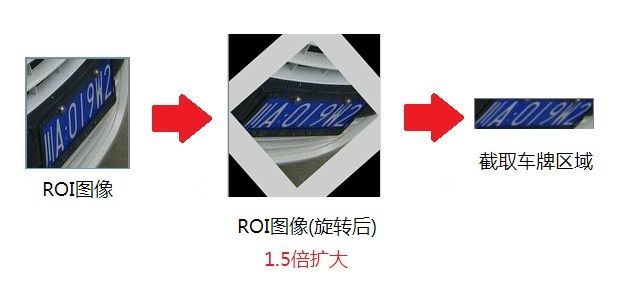
对其他的角度我们需要对ROI进行旋转。当我们对ROI进行旋转以后,接着把转正后的RotataedRect部分从ROI中截取出来。
但很快我们就会碰到一个新问题。让我们看一下下图,为什么我们截取出来的车牌区域最左边的“川”字和右边的“2”字发生了形变?为了搞清这个原因,作者仔细地研究了旋转与截取函数,但很快发现了形变的根源在于旋转后的ROI图像。
仔细看一下旋转后的ROI图像,是否左右两侧不再完整,像是被截去了一部分?
图17 旋转后图像被截断
要想理解这个问题,需要理解opencv的旋转变换函数的特性。作为旋转变换的核心函数,affinTransform会要求你输出一个旋转矩阵给它。这很简单,因为我们只需要给它一个旋转中心点以及角度,它就能计算出我们想要的旋转矩阵。旋转矩阵的获得是通过如下的函数得到的:
Mat rot_mat = getRotationMatrix2D(new_center, angle, 1);
在获取了旋转矩阵rot_mat,那么接下来就需要调用函数warpAffine来开始旋转操作。这个函数的参数包括一个目标图像、以及目标图像的Size。目标图像容易理解,大部分opencv的函数都会需要这个参数。我们只要新建一个Mat即可。那么目标图像的Size是什么?在一般的观点中,假设我们需要旋转一个图像,我们给opencv一个原始图像,以及我需要在某个旋转点对它旋转一个角度的需求,那么opencv返回一个图像给我即可,这个图像的Size或者说大小应该是opencv返回给我的,为什么要我来告诉它呢?
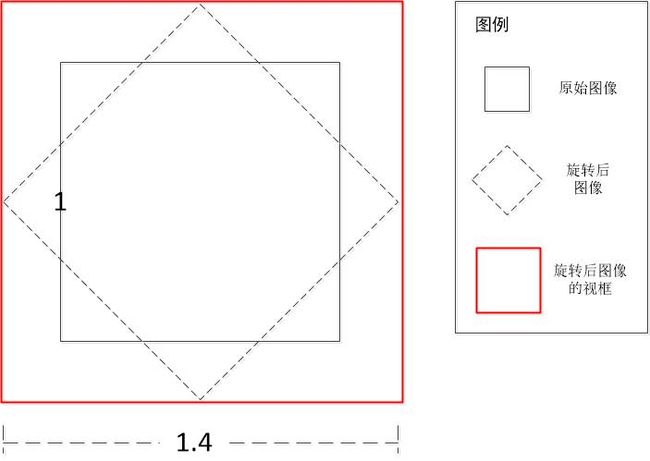
你可以试着对一个正方形进行旋转,仔细看看,这个正方形的外接矩形的大小会如何变化?当旋转角度还小时,一切都还好,当角度变大时,明显我们看到的外接矩形的大小也在扩增。在这里,外接矩形被称为视框,也就是我需要旋转的正方形所需要的最小区域。随着旋转角度的变大,视框明显增大。
图18 矩形旋转后所需视框增大
在图像旋转完以后,有三类点会获得不同的处理,一种是有原图像对应点且在视框内的,这些点被正常显示;一类是在视框内但找不到原图像与之对应的点,这些点被置0值(显示为黑色);最后一类是有原图像与之对应的点,但不在视框内的,这些点被悲惨的抛弃。
图19 旋转后三类不同点的命运
这就是旋转后不同三类点的命运,也就是新生成的图像中一些点呈现黑色(被置0),一些点被截断(被抛弃)的原因。如果把视框调整大点的话,就可以大幅度减少被截断点的数量。所以,为了保证旋转后的图像不被截断,因此我们需要计算一个合理的目标图像的Size,让我们的感兴趣区域得到完整的显示。
下面的代码使用了一个极为简单的策略,它将原始图像与目标图像都进行了扩大化。首先新建一个尺寸为原始图像1.5倍的新图像,接着把原始图像映射到新图像上,于是我们得到了一个显示区域(视框)扩大化后的原始图像。显示区域扩大以后,那些在原图像中没有值的像素被置了一个初值。
接着调用warpAffine函数,使用新图像的大小作为目标图像的大小。warpAffine函数会将新图像旋转,并用目标图像尺寸的视框去显示它。于是我们得到了一个所有感兴趣区域都被完整显示的旋转后图像。
这样,我们再使用getRectSubPix()函数就可以获得想要的车牌区域了。
图20 扩大化旋转后图像不再被截断
以下就是旋转函数rotation的代码。
//! 旋转操作 bool CPlateLocate::rotation(Mat& in, Mat& out, const Size rect_size, const Point2f center, const double angle) { Mat in_large; in_large.create(in.rows*1.5, in.cols*1.5, in.type()); int x = in_large.cols / 2 - center.x > 0 ? in_large.cols / 2 - center.x : 0; int y = in_large.rows / 2 - center.y > 0 ? in_large.rows / 2 - center.y : 0; int width = x + in.cols < in_large.cols ? in.cols : in_large.cols - x; int height = y + in.rows < in_large.rows ? in.rows : in_large.rows - y; /*assert(width == in.cols); assert(height == in.rows);*/ if (width != in.cols || height != in.rows) return false; Mat imageRoi = in_large(Rect(x, y, width, height)); addWeighted(imageRoi, 0, in, 1, 0, imageRoi); Point2f center_diff(in.cols/2, in.rows/2); Point2f new_center(in_large.cols / 2, in_large.rows / 2); Mat rot_mat = getRotationMatrix2D(new_center, angle, 1); /*imshow("in_copy", in_large); waitKey(0);*/ Mat mat_rotated; warpAffine(in_large, mat_rotated, rot_mat, Size(in_large.cols, in_large.rows), CV_INTER_CUBIC); /*imshow("mat_rotated", mat_rotated); waitKey(0);*/ Mat img_crop; getRectSubPix(mat_rotated, Size(rect_size.width, rect_size.height), new_center, img_crop); out = img_crop; /*imshow("img_crop", img_crop); waitKey(0);*/ return true; }
4.偏斜判断
当我们对ROI进行旋转以后,下面一步工作就是把RotataedRect部分从ROI中截取出来,这里可以使用getRectSubPix方法,这个函数可以在被旋转后的图像中截取一个正的矩形图块出来,并赋值到一个新的Mat中,称为车牌区域。
下步工作就是分析截取后的车牌区域。车牌区域里的车牌分为正角度和偏斜角度两种。对于正的角度而言,可以看出车牌区域就是车牌,因此直接输出即可。而对于偏斜角度而言,车牌是平行四边形,与矩形的车牌区域不重合。
如何判断一个图像中的图形是否是平行四边形?
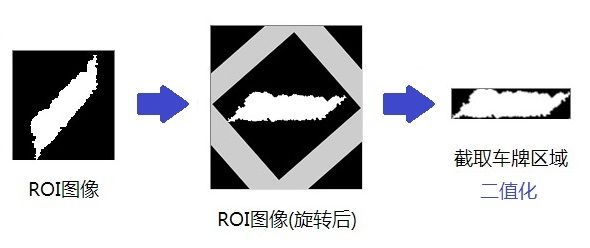
一种简单的思路就是对图像二值化,然后根据二值化图像进行判断。图像二值化的方法有很多种,假设我们这里使用一开始在车牌定位功能中使用的大津阈值二值化法的话,效果不会太好。因为大津阈值是自适应阈值,在完整的图像中二值出来的平行四边形可能在小的局部图像中就不再是。最好的办法是使用在前面定位模块生成后的原图的二值图像,我们通过同样的操作就可以在原图中截取一个跟车牌区域对应的二值化图像。
下图就是一个二值化车牌区域获得的过程。
图21 二值化的车牌区域
接下来就是对二值化车牌区域进行处理。为了判断二值化图像中白色的部分是平行四边形。一种简单的做法就是从图像中选择一些特定的行。计算在这个行中,第一个全为0的串的长度。从几何意义上来看,这就是平行四边形斜边上某个点距离外接矩形的长度。
假设我们选择的这些行位于二值化图像高度的1/4,2/4,3/4处的话,如果是白色图形是矩形的话,这些串的大小应该是相等或者相差很小的,相反如果是平行四边形的话,那么这些串的大小应该不等,并且呈现一个递增或递减的关系。通过这种不同,我们就可以判断车牌区域里的图形,究竟是矩形还是平行四边形。
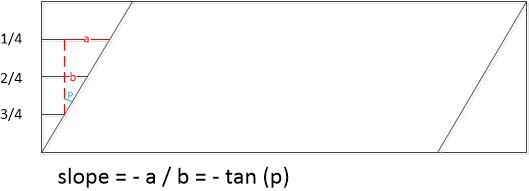
偏斜判断的另一个重要作用就是,计算平行四边形倾斜的斜率,这个斜率值用来在下面的仿射变换中发挥作用。我们使用一个简单的公式去计算这个斜率,那就是利用上面判断过程中使用的串大小,假设二值化图像高度的1/4,2/4,3/4处对应的串的大小分别为len1,len2,len3,车牌区域的高度为Height。一个计算斜率slope的计算公式就是:(len3-len1)/Height*2。
Slope的直观含义见下图。
图22 slope的几何含义
需要说明的,这个计算结果在平行四边形是右斜时是负值,而在左斜时则是正值。于是可以根据slope的正负判断平行四边形是右斜或者左斜。在实践中,会发生一些公式不能应对的情况,例如像下图这种情况,斜边的部分区域发生了内凹或者外凸现象。这种现象会导致len1,len2或者len3的计算有误,因此slope也会不准。
图23 内凹现象
为了实现一个鲁棒性更好的计算方法,可以用(len2-len1)/Height*4与(len3-len1)/Height*2两者之间更靠近tan(angle)的值作为solpe的值(在这里,angle代表的是原来RotataedRect的角度)。
多采取了一个slope备选的好处是可以避免单点的内凹或者外凸,但这仍然不是最好的解决方案。在最后的讨论中会介绍一个其他的实现思路。
完成偏斜判断与斜率计算的函数是isdeflection,下面是它的代码。
//! 是否偏斜 //! 输入二值化图像,输出判断结果 bool CPlateLocate::isdeflection(const Mat& in, const double angle, double& slope) { int nRows = in.rows; int nCols = in.cols; assert(in.channels() == 1); int comp_index[3]; int len[3]; comp_index[0] = nRows / 4; comp_index[1] = nRows / 4 * 2; comp_index[2] = nRows / 4 * 3; const uchar* p; for (int i = 0; i < 3; i++) { int index = comp_index[i]; p = in.ptr(index); int j = 0; int value = 0; while (0 == value && j < nCols) value = int(p[j++]); len[i] = j; } //cout << "len[0]:" << len[0] << endl; //cout << "len[1]:" << len[1] << endl; //cout << "len[2]:" << len[2] << endl; double maxlen = max(len[2], len[0]); double minlen = min(len[2], len[0]); double difflen = abs(len[2] - len[0]); //cout << "nCols:" << nCols << endl; double PI = 3.14159265; double g = tan(angle * PI / 180.0); if (maxlen - len[1] > nCols/32 || len[1] - minlen > nCols/32 ) { // 如果斜率为正,则底部在下,反之在上 double slope_can_1 = double(len[2] - len[0]) / double(comp_index[1]); double slope_can_2 = double(len[1] - len[0]) / double(comp_index[0]); double slope_can_3 = double(len[2] - len[1]) / double(comp_index[0]); /*cout << "slope_can_1:" << slope_can_1 << endl; cout << "slope_can_2:" << slope_can_2 << endl; cout << "slope_can_3:" << slope_can_3 << endl;*/ slope = abs(slope_can_1 - g) <= abs(slope_can_2 - g) ? slope_can_1 : slope_can_2; /*slope = max( double(len[2] - len[0]) / double(comp_index[1]), double(len[1] - len[0]) / double(comp_index[0]));*/ //cout << "slope:" << slope << endl; return true; } else { slope = 0; } return false; }
5.仿射变换
俗话说:行百里者半九十。前面已经做了如此多的工作,应该可以实现偏斜扭转功能了吧?但在最后的道路中,仍然有问题等着我们。
我们已经实现了旋转功能,并且在旋转后的区域中截取了车牌区域,然后判断车牌区域中的图形是一个平行四边形。下面要做的工作就是把平行四边形扭正成一个矩形。
图24 从平行四边形车牌到矩形车牌
首先第一个问题就是解决如何从平行四边形变换成一个矩形的问题。opencv提供了一个函数warpAffine,就是仿射变换函数。注意,warpAffine不仅可以让图像旋转(前面介绍过),也可以进行仿射变换,真是一个多才多艺的函数。o
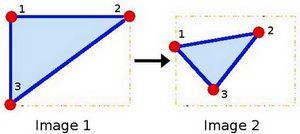
通过仿射变换函数可以把任意的矩形拉伸成其他的平行四边形。opencv的官方文档里给了一个示例,值得注意的是,这个示例演示的是把矩形变换为平行四边形,跟我们想要的恰恰相反。但没关系,我们先看一下它的使用方法。
图25 opencv官网上对warpAffine使用的示例
warpAffine方法要求输入的参数是原始图像的左上点,右上点,左下点,以及输出图像的左上点,右上点,左下点。注意,必须保证这些点的对应顺序,否则仿射的效果跟你预想的不一样。通过这个方法介绍,我们可以大概看出,opencv需要的是三个点对(共六个点)的坐标,然后建立一个映射关系,通过这个映射关系将原始图像的所有点映射到目标图像上。
图26 warpAffine需要的三个对应坐标点
再回来看一下我们的需求,我们的目标是把车牌区域中的平行四边形映射为一个矩形。让我们做个假设,如果我们选取了车牌区域中的平行四边形车牌的三个关键点,然后再确定了我们希望将车牌扭正成的矩形的三个关键点的话,我们是否就可以实现从平行四边形车牌到矩形车牌的扭正?
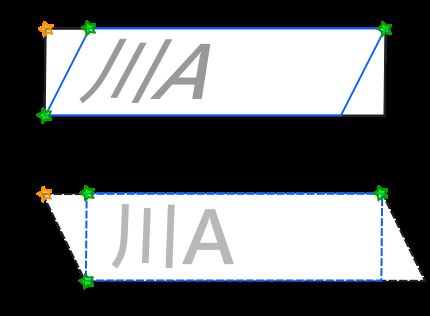
让我们画一幅图像来看看这个变换的作用。有趣的是,把一个平行四边形变换为矩形会对包围平行四边形车牌的区域带来影响。
例如下图中,蓝色的实线代表扭转前的平行四边形车牌,虚线代表扭转后的。黑色的实线代表矩形的车牌区域,虚线代表扭转后的效果。可以看到,当蓝色车牌被扭转为矩形的同时,黑色车牌区域则被扭转为平行四边形。
注意,当车牌区域扭变为平行四边形以后,需要显示它的视框增大了。跟我们在旋转图像时碰到的情形一样。
图27 平行四边形的扭转带来的变化
让我们先实际尝试一下仿射变换吧。
根据仿射函数的需要,我们计算平行四边形车牌的三个关键点坐标。其中左上点的值(xdiff,0)中的xdiff就是根据车牌区域的高度height与平行四边形的斜率slope计算得到的:
xidff = Height * abs(slope)
为了计算目标矩形的三个关键点坐标,我们首先需要把扭转后的原点坐标调整到平行四边形车牌区域左上角位置。见下图。
图28 原图像的坐标计算
依次推算关键点的三个坐标。它们应该是
plTri[0] = Point2f(0 + xiff, 0); plTri[1] = Point2f(width - 1, 0); plTri[2] = Point2f(0, height - 1); dstTri[0] = Point2f(xiff, 0); dstTri[1] = Point2f(width - 1, 0); dstTri[2] = Point2f(xiff, height - 1);
根据上图的坐标,我们开始进行一次仿射变换的尝试。
opencv的warpAffine函数不会改变变换后图像的大小。而我们给它传递的目标图像的大小仅会决定视框的大小。不过这次我们不用担心视框的大小,因为根据图27看来,哪怕视框跟原始图像一样大,我们也足够显示扭正后的车牌。
看看仿射的效果。晕,好像效果不对,视框的大小是足够了,但是图像往右偏了一些,导致最右边的字母没有显示全。
图29 被偏移的车牌区域
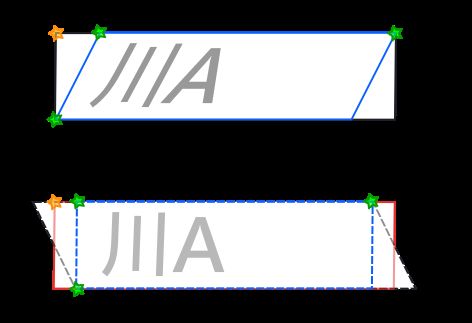
这次的问题不再是目标图像的大小问题了,而是视框的偏移问题。仔细观察一下我们的视框,倘若我们想把车牌全部显示的话,视框往右偏移一段距离,是不是就可以解决这个问题呢?为保证新的视框中心能够正好与车牌的中心重合,我们可以选择偏移xidff/2长度。正如下图所显示的一样。
图30 考虑偏移的坐标计算
视框往右偏移的含义就是目标图像Mat的原点往右偏移。如果原点偏移的话,那么仿射后图像的三个关键点的坐标要重新计算,都需要减去xidff/2大小。
重新计算的映射点坐标为下:
plTri[0] = Point2f(0 + xiff, 0); plTri[1] = Point2f(width - 1, 0); plTri[2] = Point2f(0, height - 1); dstTri[0] = Point2f(xiff/2, 0); dstTri[1] = Point2f(width - 1 - xiff + xiff/2, 0); dstTri[2] = Point2f(xiff/2, height - 1);
再试一次。果然,视框被调整到我们希望的地方了,我们可以看到所有的车牌区域了。这次解决的是warpAffine函数带来的视框偏移问题。
图31 完整的车牌区域
关于坐标调整的另一个理解就是当中心点保持不变时,平行四边形扭正为矩形时恰好是左上的点往左偏移了xdiff/2的距离,左下的点往右偏移了xdiff/2的距离,形成一种对称的平移。可以使用ps或者inkspace类似的矢量制图软件看看“斜切”的效果,
如此一来,就完成了偏斜扭正的过程。需要注意的是,向左倾斜的车牌的视框偏移方向与向右倾斜的车牌是相反的。我们可以用slope的正负来判断车牌是左斜还是右斜。
6.总结
通过以上过程,我们成功的将一个偏斜的车牌经过旋转变换等方法扭正过来。
让我们回顾一下偏斜扭正过程。我们需要将一个偏斜的车牌扭正,为了达成这个目的我们首先需要对图像进行旋转。因为旋转是个计算量很大的函数,所以我们需要考虑不再用全图旋转,而是区域旋转。在旋转过程中,会发生图像截断问题,所以需要使用扩大化旋转方法。旋转以后,只有偏斜视角的车牌才需要扭正,正视角的车牌不需要,因此还需要一个偏斜判断过程。如此一来,偏斜扭正的过程需要旋转,区域截取,扩大化,偏斜判断等等过程的协助,这就是整个流程中有这么多步需要处理的原因。
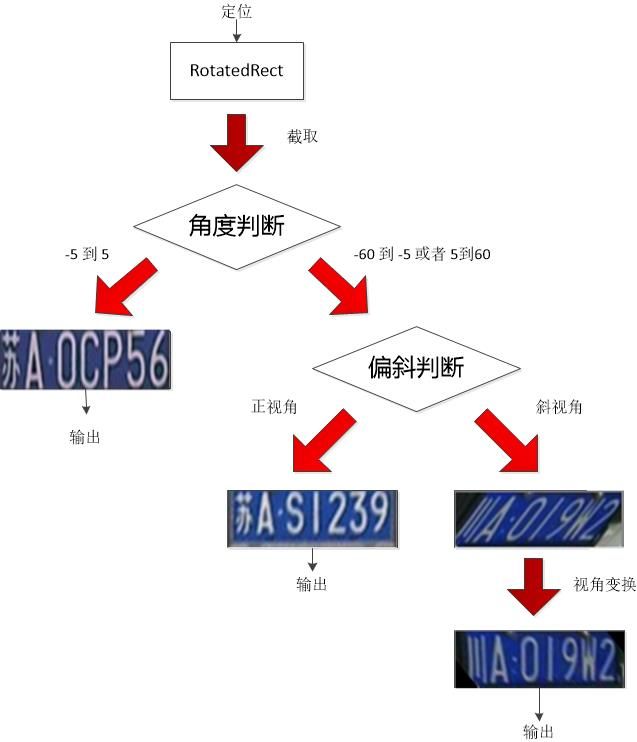
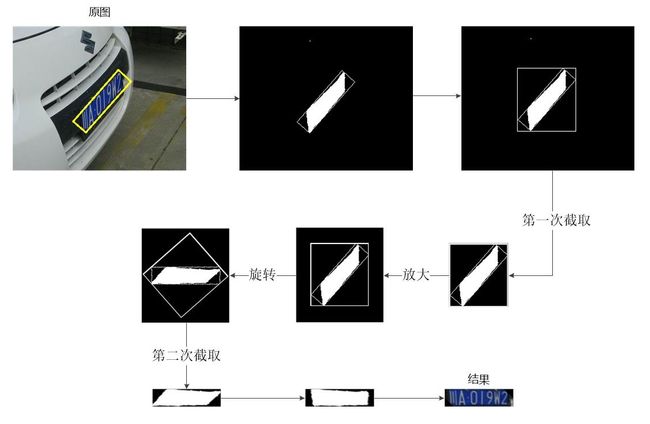
下图从另一个视角回顾了偏斜扭正的过程,主要说明了偏斜扭转中的两次“截取”过程。
图32 偏斜扭正全过程
- 首先我们获取RotatedRect,然后对每个RotatedRect获取外界矩形,也就是ROI区域。外接矩形的计算有可能获得不安全的坐标,因此需要使用安全的获取外界矩形的函数。
- 获取安全外接矩形以后,在原图中截取这部分区域,并放置到一个新的Mat里,称之为ROI图像。这是本过程中第一次截取,使用Mat(Rect ...)函数。
- 接下来对ROI图像根据RotatedRect的角度展开旋转,旋转的过程中使用了放大化旋转法,以此防止车牌区域被截断。
- 旋转完以后,我们把已经转正的RotatedRect部分截取出来,称之为车牌区域。这是本过程中第二次截取,与第一次不同,这次截取使用getRectSubPix()方法。
- 接下里使用偏斜判断函数来判断车牌区域里的车牌是否是倾斜的。
- 如果是,则继续使用仿射变换函数wrapAffine来进行扭正处理,处理过程中要注意三个关键点的坐标。
- 最后使用resize函数将车牌区域统一化为EasyPR的车牌大小。
整个过程有一个统一的函数--deskew。下面是deskew的代码。
//! 抗扭斜处理 int CPlateLocate::deskew(const Mat& src, const Mat& src_b, vector& inRects, vector & outPlates) { for (int i = 0; i < inRects.size(); i++) { RotatedRect roi_rect = inRects[i]; float r = (float)roi_rect.size.width / (float)roi_rect.size.height; float roi_angle = roi_rect.angle; Size roi_rect_size = roi_rect.size; if (r < 1) { roi_angle = 90 + roi_angle; swap(roi_rect_size.width, roi_rect_size.height); } if (roi_angle - m_angle < 0 && roi_angle + m_angle > 0) { Rect_<float> safeBoundRect; bool isFormRect = calcSafeRect(roi_rect, src, safeBoundRect); if (!isFormRect) continue; Mat bound_mat = src(safeBoundRect); Mat bound_mat_b = src_b(safeBoundRect); Point2f roi_ref_center = roi_rect.center - safeBoundRect.tl(); Mat deskew_mat; if ((roi_angle - 5 < 0 && roi_angle + 5 > 0) || 90.0 == roi_angle || -90.0 == roi_angle) { deskew_mat = bound_mat; } else { // 角度在5到60度之间的,首先需要旋转 rotation Mat rotated_mat; Mat rotated_mat_b; if (!rotation(bound_mat, rotated_mat, roi_rect_size, roi_ref_center, roi_angle)) continue; if (!rotation(bound_mat_b, rotated_mat_b, roi_rect_size, roi_ref_center, roi_angle)) continue; // 如果图片偏斜,还需要视角转换 affine double roi_slope = 0; if (isdeflection(rotated_mat_b, roi_angle, roi_slope)) { //cout << "roi_angle:" << roi_angle << endl; //cout << "roi_slope:" << roi_slope << endl; affine(rotated_mat, deskew_mat, roi_slope); } else deskew_mat = rotated_mat; } Mat plate_mat; plate_mat.create(HEIGHT, WIDTH, TYPE); if (deskew_mat.cols >= WIDTH || deskew_mat.rows >= HEIGHT) resize(deskew_mat, plate_mat, plate_mat.size(), 0, 0, INTER_AREA); else resize(deskew_mat, plate_mat, plate_mat.size(), 0, 0, INTER_CUBIC); /*if (1) { imshow("plate_mat", plate_mat); waitKey(0); destroyWindow("plate_mat"); }*/ CPlate plate; plate.setPlatePos(roi_rect); plate.setPlateMat(plate_mat); outPlates.push_back(plate); } } return 0; }
最后是改善建议:
角度偏斜判断时可以用白色区域的轮廓来确定平行四边形的四个点,然后用这四个点来计算斜率。这样算出来的斜率的可能鲁棒性更好。
三. 总结
本篇文档介绍了颜色定位与偏斜扭转等功能。其中颜色定位属于作者一直想做的定位方法,而偏斜扭转则是作者以前认为不可能解决的问题。这些问题现在都基本被攻克了,并在这篇文档中阐述,希望这篇文档可以帮助到读者。
作者希望能在这片文档中不仅传递知识,也传授我在摸索过程中积累的经验。因为光知道怎么做并不能加深对车牌识别的认识,只有经历过失败,了解哪些思想尝试过,碰到了哪些问题,是如何解决的,才能帮助读者更好地认识这个系统的内涵。
最后,作者很感谢能够阅读到这里的读者。如果看完觉得好的话,还请轻轻点一下赞,你们的鼓励就是作者继续行文的动力。
对EasyPR做下说明:EasyPR,一个开源的中文车牌识别系统,代码托管在github。其次,在前面的博客文章中,包含EasyPR至今的开发文档与介绍。在后续的文章中,作者会介绍EasyPR中字符分割与识别等相关内容,欢迎继续阅读。
版权说明:
本文中的所有文字,图片,代码的版权都是属于作者和博客园共同所有。欢迎转载,但是务必注明作者与出处。任何未经允许的剽窃以及爬虫抓取都属于侵权,作者和博客园保留所有权利。
参考文献:
1.http://blog.csdn.net/xiaowei_cqu/article/details/7616044
2.http://docs.opencv.org/doc/tutorials/imgproc/imgtrans/warp_affine/warp_affine.html